CRYPTO现代密码学学习
RC4 加密算法
简单介绍:RC4加密算法是一种对称加密算法,加密和解密使用同一个函数
初始化分为以下几个步骤
- 初始化存储0-255字节的Sbox(其实就是一个数组)
- 填充key到256个字节数组中称为Tbox(你输入的key不满256个字节则初始化到256个字节)
- 交换s[i]与s[j] i 从0开始一直到255下标结束. j是 s[i]与T[i]组合得出的下标
// 步骤一、初始化赋值 for (i=0;i<256;i++){ S[i] = i; T[I] = K[i mod keylen]; } // 步骤二、用T产生S的初始置换 j = 0; for (i=0; i<256; i++) { j = (j + S[i] + T[i]) mod 256; swap(S[i],S[j]); } // 步骤三、得到密钥流K(每次计算出一个K) i=j=0; for(h=0; h<datalen; h++) { i=(i+1) mod 256; j=(j+S[i]) mod 256; swap(S[i],s[j]); t=(S[i]+S[j]) mod 256; K=S[t]; // D[h]^=K; 亦或得到密文 } ```
RSA加密解密

求解私钥的步骤:
欧拉函数:表示表示与n互质的数的个数

eg:
[WUSTCTF2020]babyrsa
c = 28767758880940662779934612526152562406674613203406706867456395986985664083182
n = 73069886771625642807435783661014062604264768481735145873508846925735521695159
e = 65537
若要求解私钥,必须要分解n,得到两个质数p,q:http://www.factordb.com/index.php
p = 189239861511125143212536989589123569301
q = 386123125371923651191219869811293586459
求解私钥d,以及明文m
from Crypto.Util.number import long_to_bytes
from Crypto.Util.number import *
q = 189239861511125143212536989589123569301
p = 386123125371923651191219869811293586459
e = 65537
c = 28767758880940662779934612526152562406674613203406706867456395986985664083182
# n = 73069886771625642807435783661014062604264768481735145873508846925735521695159
n = q * p
# print(n)
d = gmpy2.invert(e, (p - 1) * (q - 1))
print("d=", d)
m = pow(c, d, n)
此处有疑问了,明文是如何转为这么一大长串数字呢?
import Crypto
from Crypto.Util.number import bytes_to_long
import os
t = os.urandom(4) # os.urandom(len)方式产生长度为len的随机字节串
print(t)
for i in t:
print(i)
print(bytes_to_long(t)) # 调用函数计算long整型值:
计算原理:29*pow(2,24) + 30*pow(2,16) + 150*pow(2,8) + 148*pow(2,0)
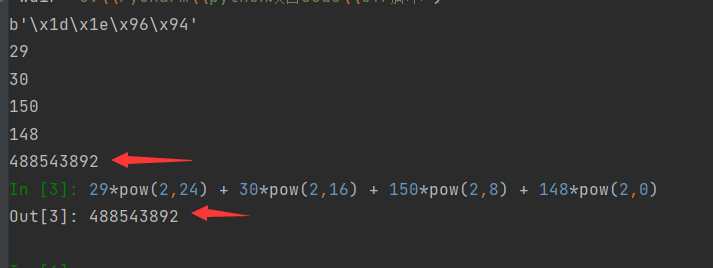
大数在此处的类是mpz,引用了GMP库:参考传送阵
判断字符串中所有字符是否都是可打印字符。
Unicode字符集中“Other” “Separator”类别的字符为不可打印的字符(但不包括ASCII码中的空格(0x20))。可用于判断转义字符。
ASCII码中第0~32号及第127号是控制字符;第33~126号是可打印字符,其中第48~57号为0~9十个阿拉伯数字;65~90号为26个大写英文字母,97~
122号为26个小写英文字母。
ascii码在0~255字符中只有189个字符能被打印。
lst = []
for idx,val in enumerate(range(256)):
if chr(val).isprintable():
lst.append(idx)
print(len(lst))
print(set(range(256)) - set(lst))

DES加密解密详解
Data Encryption Standard
就不主动写了,这篇文章讲的非常详细:
https://www.hankcs.com/security/des-algorithm-illustrated.html
密钥的生成
- 子密钥
K1~K16的生成:
密钥转为2进制的初始密钥,初始密钥进行PC-1置换,得到56位的密钥;
将这56bit密钥均分为两个28bit,左半部分 (C0) ,右半部分 (D0);
将得到的 C0,D0 按照给定的移位表依次进行移位 ;
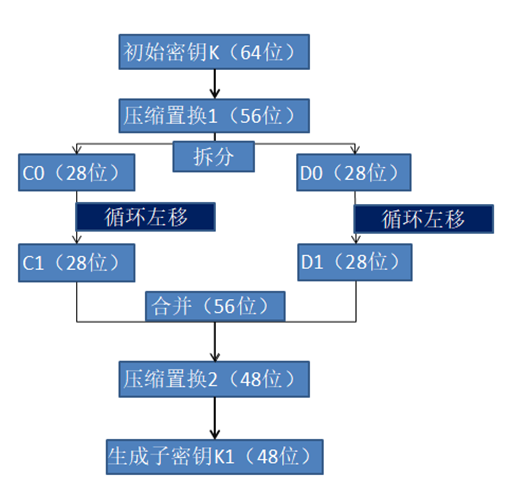
- 子密钥的Ci,Di 轮,是由 Ci-1,Di-1 循环移位运算得到的
????即off = [1, 1, 2, 2, 2, 2, 2, 2, 1, 2, 2, 2, 2, 2, 2, 1]C1为C0向左循环移位1,D1为D0向左循环移位1;C2为C1向左循环移位1,D2为D1向左循环移位1;C3为C2向左循环移位2,D3为D2向左循环移位2;最后将其 Ci 与 Di 合并为 CiDi 。 - 将合并后的每个 CiDi 经过
PC-2置换,得到K1~K16。
密文的生成
-
和密钥的生成一样,先进行一个初始置换(换了个名字,叫IP置换)只不过密钥是将校验位去掉了,而明文的加密不需要验证。
-
初始置换后将其均分为左边
32位L0,右边32位R0。 -
密文的加密规则如下图
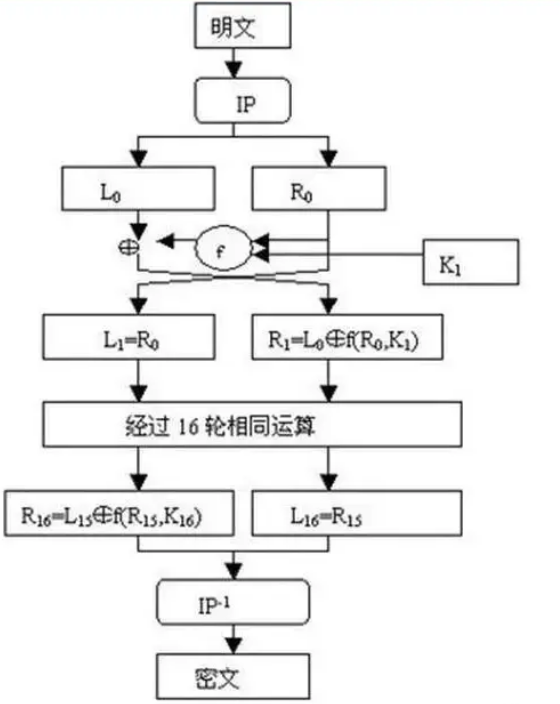
-
需要经过f函数的加密
16轮,得到的 L16 R16, 接着再次进行一个IP逆置换,形成最终的密文。 -
重要的就是这
16轮的加密。
加密函数
????Ln = Rn-1
????Rn= Ln-1 十 f (Rn-1,Kn)
f函数步骤如下(eg):- L1 = R0,R1 =L0 十 f(R0,K1)
- R0 为
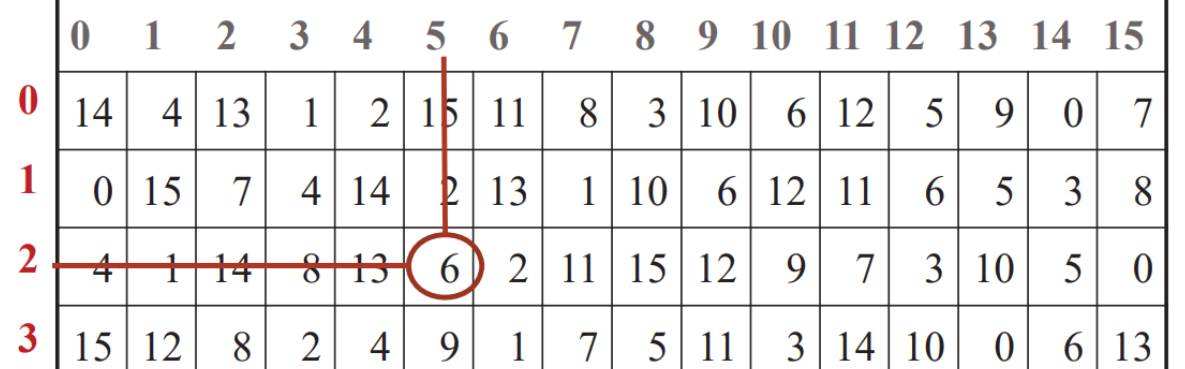
32位,K1为48位,所以要进行32-48位的E盒扩展;
扩展规则:以4为单位,分为8组,每组首位前添加前相邻位,末位后添加相邻位,如下图所示: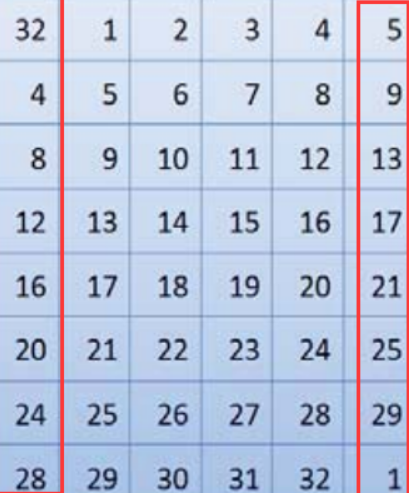
- 扩展为
48位后,与对应的子密钥进行亦或,即 R0 十 K1,得到另一组最终48位的数据。 - 分开后的密文序列是
32位的,所以还要对其进行S盒压缩,最终将8组6bit的数据被转换为8组4bit(一共32位)的数据。
将48位数据化为8组6bit:B1B2B3B4B5B6B7B8 ,每组含有6bit,经过以下运算
????S1(B1)S2(B2)S3(B3)S4(B4)S5(B5)S6(B6)S7(B7)S8(B8)
最终得到的8组6bit的数据
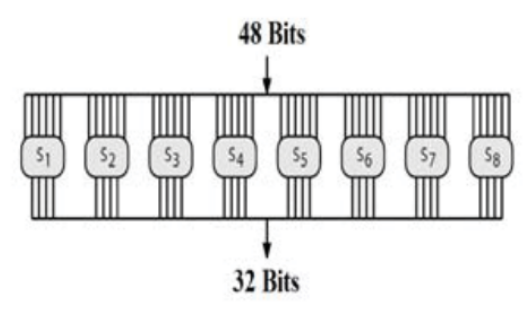
S盒计算eg:
101010到S1中。S1会将这六位的第一位1和第六位0拿出来,组成10作为S1的行,中间四位0101拿出来作为S1的列。我们转换成十进制,此时映射到这个S盒的位置就是(2,5),对应S盒的第3行第6列(索引都从0开始数)。
- 将得到的
32位数据在经过P盒置换,得到数据即为f函数结束
-
将最终经过
f函数的数据与 L0 亦或,得到 R1,即 L0 十 上一步结果 -
重复上面步骤至
16轮,在第16轮后,将R16 与 L16 拼接为 R16L16。 -
R16L16 经过
IP-1盒逆置换,得到最终16进制数,即为密文。
注意:
DES加密算法中,
- 密钥:
置换PC-1盒,64位去掉校验位为56位,简单表替换;
置换PC-2盒,取56位密钥中的48位,简单表替换 - 密文:
置换IP盒,将原明文数据打乱,简单表替换,数据位数不变;
扩展E盒,将分开的32位扩展为48位;
压缩S盒,将已经经过f函数变换后的48位数据(8组6bit)变回原来的32位(8组4bit),用于下次f函数的计算 ;
置换P盒,将S盒的到的数据进行置换,简单表替换,数据位数依旧为32位。经P盒置换后的数据和 L0 做 十 ,得到下一步的 Ri+1 .
逆置换IP-1盒,合并后 R16L16 简单表替换,数据位数不变64bit。
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
- Python教程
- 深入理解 MySQL 中的 HAVING 关键字和聚合函数
- Qt之QChar编码(1)
- MyBatis入门基础篇
- 用Python脚本实现FFmpeg批量转换
- 阿里云SLS日志服务之数据导入与加工处理
- 传感器原理与应用复习
- 2024.1.10 SparkSQL ,函数分类, Spark on HIVE,底层执行流程
- IOC之Spring统一资源加载策略
- 装配铸铁平台怎样来排除故障——河北北重
- 凯撒密码
- pytorch 通用训练代码讲解(very good)
- python3处理xls并flask显示
- 基于springboot+vue的小区物业管理系统(有文档、Java毕业设计)
- Qt/C++音视频开发61-多屏渲染/一个解码渲染到多个窗口/画面实时同步