MATLAB - 最优控制（Optimal Control）

系列文章目录

---

前言 -?什么是最优控制？

????????最优控制是动态系统满足设计目标的条件。最优控制是通过执行以下定义的最优性标准的控制律来实现的。一些广泛使用的最优控制方法有：

• 线性二次调节器 (LQR)/线性二次高斯 (LQG) 控制

• 模型预测控制

• 强化学习

• 极值搜索控制

• H 无穷综合

---

一、线性二次调节器 (LQR)/线性二次高斯 (LQG) 控制

线性二次调节器 (LQR) 是一种全状态反馈最优控制律，，通过最小化二次代价函数来调节控制系统。

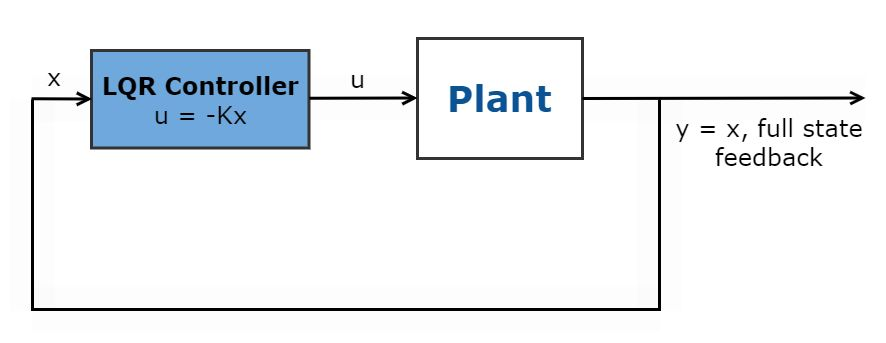
此代价函数取决于系统状态?(x)(�)?和控制输入?(u)(�)，如下所示。?

基于性能设定，为此最优控制律设置加权因子 Q、R 和 N，以定义系统状态调节和控制作动成本之间的适当平衡。

在许多最优控制问题中，并非所有状态可测量。在这些情况下，必须使用观测器来估计状态。卡尔曼滤波器就是使用频率较高的一个观测器。卡尔曼滤波器结合 LQR 控制器构成一个线性二次高斯 (LQG) 控制器。

?

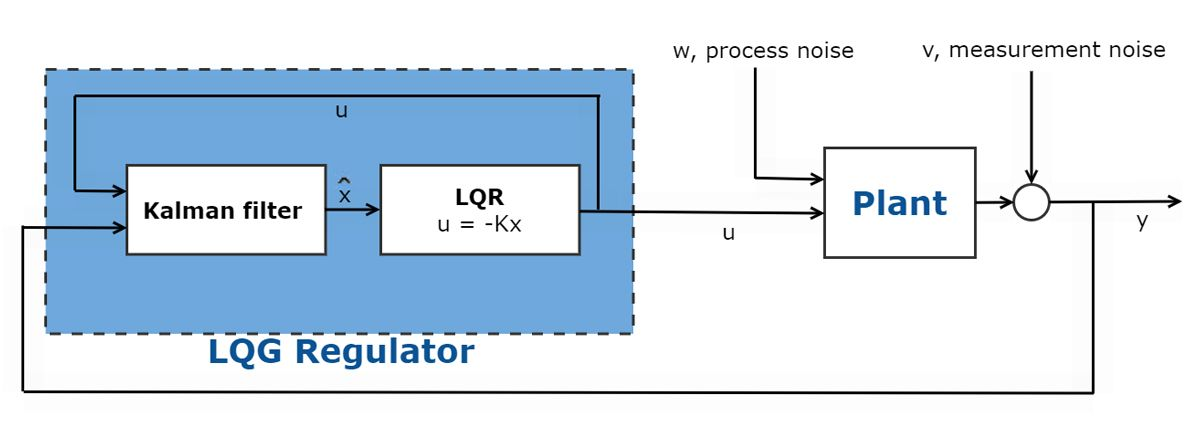
二、模型预测控制

模型预测控制 (MPC) 用于最小化多输入多输出 (MIMO) 系统中的代价函数。该系统受限于输入和输出约束。这种最优控制方法使用系统模型来预测被控对象输出。控制器使用预测的被控对象输出求解在线优化问题，即二次规划，以确定可将预测输出驱动到参考值的可操作变量的最佳调整。MPC 变体包括自适应、增益调度和非线性 MPC 控制器。所使用的 MPC 控制器的类型取决于预测模型（线性/非线性）、约束（线性/非线性）、代价函数（二次/非二次）、吞吐量和采样时间。

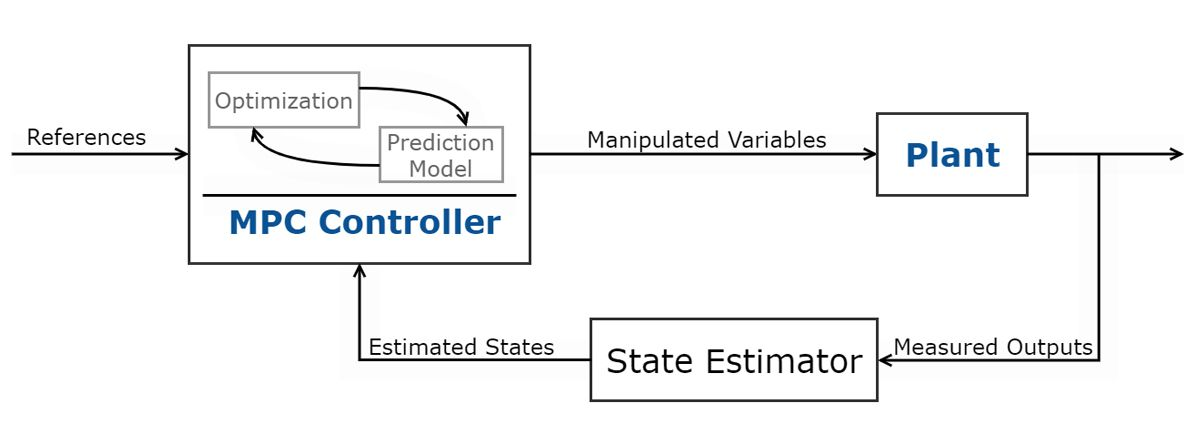
微处理器技术和高效算法的进步，使得这种最优控制方法在诸如自动驾驶、航空航天应用中的最佳地形跟踪等应用中得到了更广泛的采用。

三、强化学习

强化学习是一种机器学习方法，其中计算机智能体通过与动态环境的反复试错交互来学习最佳行为。智能体使用来自环境的观测值来执行一系列动作，目的是最大化智能体的任务累积奖励度量。这种学习不需要人工干预，也不需要显式编程。?

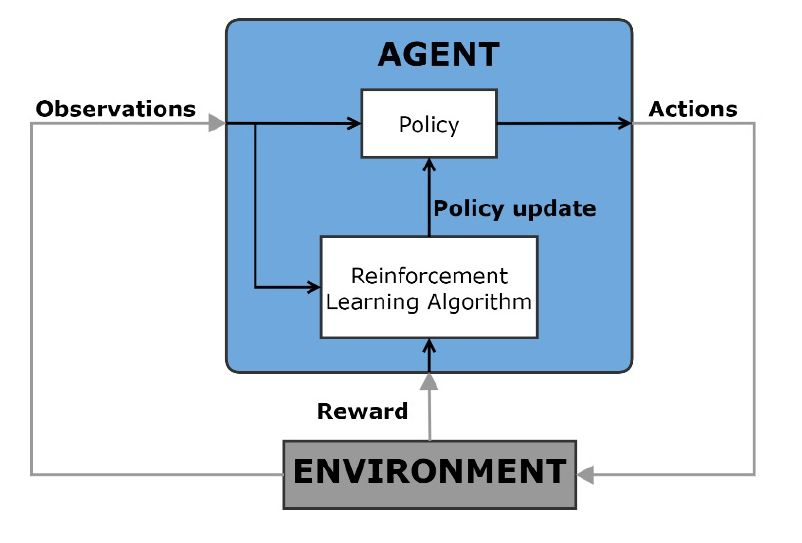
这种最优控制方法可用于决策问题，以及用作使用传统控制方法的应用的非线性控制备选方案。这些应用包括自动驾驶、机器人、调度问题和系统的动态标定等。?

四、极值搜索控制

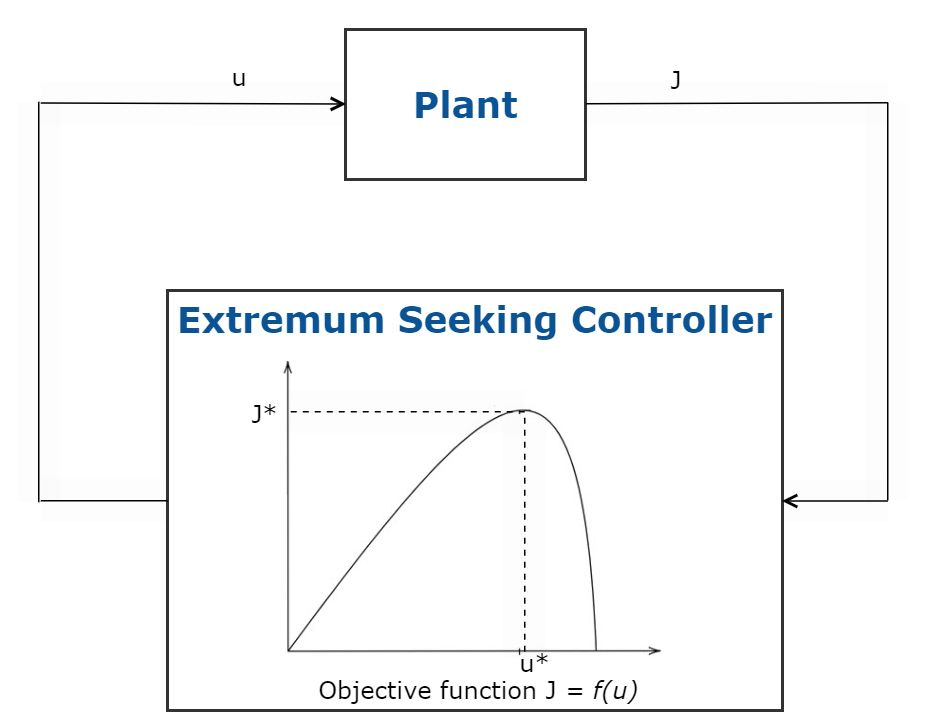
极值搜索是一种最优控制方法，它使用无模型实时优化自动调整控制系统参数以最大化目标函数。此方法不需要系统模型，可用于参数和扰动随时间缓慢变化的系统。这种最优控制方法适用于稳定的系统。这些系统可以容忍控制中的噪声，并且只需调整少量的控制系统参数。

极值搜索控制的应用包括自适应巡航控制、太阳能电池板的最大功率点追踪 (MPPT) 和防抱死制动系统 (ABS)。

?

五、H 无穷综合

H 无穷综合是一种最优控制工具/方法，用于设计单输入单输出 (SISO) 或 MIMO 反馈控制器，以实现稳健的性能和稳定性。与使用波特或 PID 调节的回路成形等经典控制方法相比，H 无穷更适合需要通道间交叉耦合的多变量控制系统。

对于 H 无穷，控制目标是根据归一化闭环增益来制定的。H 无穷综合会自动计算通过最小化该增益来优化性能的控制器。这很有用，因为许多控制目标可以用最小化增益来表示。其中包括抗扰、对噪声的灵敏度、跟踪、回路成形、回路解耦和稳健稳定性等目标。H 无穷综合的变体可用于处理固定结构或全阶控制器。

---

下表对上述最优控制方法进行了比较：

最优控制方法	优化是否在运行时进行？（是/否）	此最优控制过程的优化过程是如何工作的？	它是否能处理硬约束？*（可以/不能）	它是否使用基于模型的方法？（是/否）	吞吐量如何？（高/低）
LQR/LQG	否	使用适用于已知线性时不变系统的闭式解	不能	是	高
	隐式 MPC（是）	使用预测模型，求解在线优化问题以计算最优控制动作	可以	是	低（非线性 MPC），高（线性 MPC）
	显式 MPC（否）	用于计算最优控制动作的优化问题的解采用离线计算	是	可以	高
强化学习	是**	学习任务的最优行为以最大化奖励度量	不能***	取决于训练算法	低（使用训练）、中高（在推断过程中）
极值搜索控制	是	扰动和调整控制参数以最大化目标函数	不能	否	高
H 无穷综合	否	自动计算控制器，使其最小化归一化闭环增益	不能	是	高