DP-背包问题

01背包问题

n个物品，背包体积为V。

我们可以用是否选择了第i个物品作为状态转移的依据。我们将当前的状态定义为：“只在前i个物品中选，已使用体积为j”，这个状态可以由两个状态得到：“选择了第i个物品”和“未选择第i个物品”。

如下图所示，可以列出状态转移方程：

结合状态转移方程可知，我们可以用一个二维数组来实现这个过程。

#include<iostream>
#include<algorithm>
using namespace std;
int main()
{
    int N,V,v[1010],w[1010],f[1010][1010];
    scanf("%d%d",&N,&V);
    for(int i=1;i<=N;i++) scanf("%d%d",&v[i],&w[i]);
    
    for(int i=1;i<=N;i++)
    {
        for(int j=0;j<=V;j++)
        {
            f[i][j]=f[i-1][j];
            if(j>=v[i]) f[i][j]=max(f[i-1][j],f[i-1][j-v[i]]+w[i]);
        }
    }
    printf("%d",f[N][V]);
}

在这里有一个优化，可以发现，每次更新状态时，其实只需要用到第i-1层的状态，因此，我们没有必要将此前的0~i-2层都保存下来，我们可以直接去掉第一维。因为当更新第i维时，f值正好处于i-1维，若直接去掉，有：

f[j]=max(f[j], f[j-v[i]]+w[i])

也就是说，我们需要用f[j-v[i]]这个状态来更新f[j]，因此要后更新f[j-v[i]]，所以此时我们对j的遍历应该是从V开始，而不是从0开始。

最后的代码如下：

#include<iostream>
using namespace std;
const int N=1010;
int n,V;
int v[N],w[N];
int f[N];
int main()
{
    scanf("%d%d",&n,&V);
    for(int i=1;i<=n;i++) scanf("%d%d",&v[i],&w[i]);
    for(int i=0;i<=n;i++)
        for(int j=V;j>=v[i];j--)
        {
            f[j]=max(f[j], f[j-v[i]]+w[i]);
        }
    printf("%d",f[V]);
}

完全背包问题

n种物品，每种物品有无限个，背包体积为V。

我们用是否选择了第i个物品作为状态转移的依据。将当前的状态定义为：“只在前i个物品中选，已使用体积为j”，这个状态可以由多个状态得到：“选择了第0，1，2.....x个第i种物品”。

如下图所示，可以列出状态转移方程：

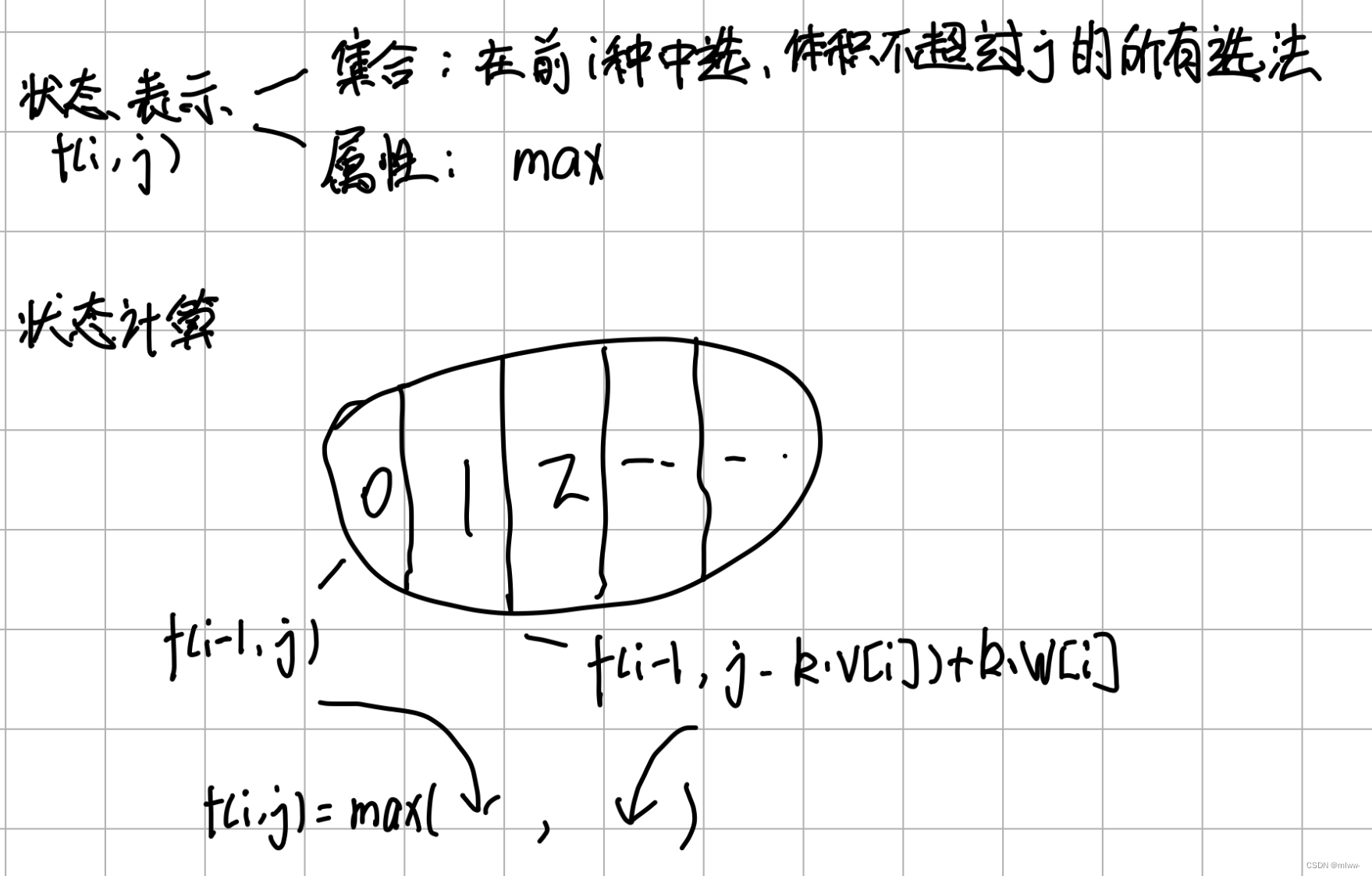
根据状态转移方程，我们需要三重循环，时间复杂度很高，接下来进行优化。优化过程如下：

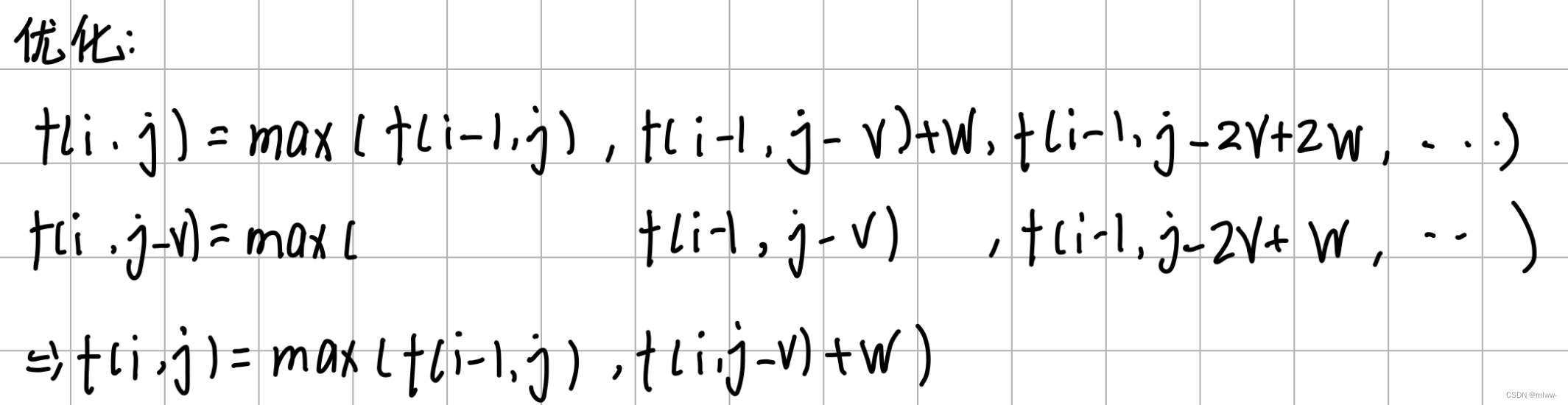
这样一来，只需要两重循环了，最后可以像01背包问题一样，将数组优化到1维。

#include<iostream>
using namespace std;
const int N=1010;
int n,V;
int v[N],w[N];
int f[N];
int main()
{
    scanf("%d%d",&n,&V);
    for(int i=1;i<=n;i++) scanf("%d%d",&v[i],&w[i]);
    for(int i=1;i<=n;i++)
        for(int j=v[i];j<=V;j++)
        {
                f[j]=max(f[j],f[j-v[i]]+w[i]);
        }
    printf("%d",f[V]);       
}

而

多重背包问题

n种物品，每种物品有s个，背包体积为V。

我们用是否选择了第i个物品作为状态转移的依据。将当前的状态定义为：“只在前i个物品中选，已使用体积为j”，这个状态可以由多个状态得到：“选择了第0，1，2.....s个第i种物品”。

如下图所示，可以列出状态转移方程：

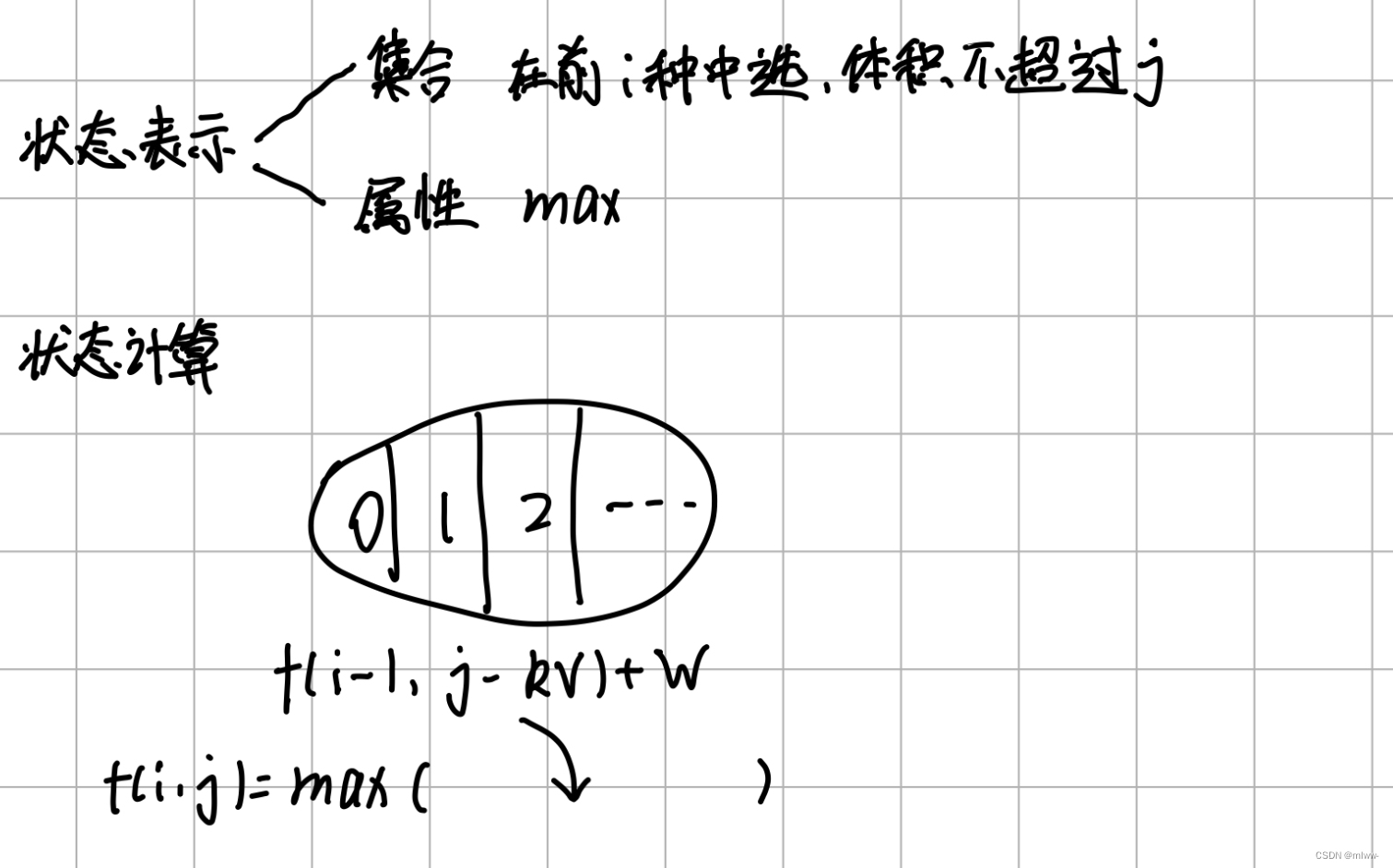
在这里，我们用到了三层循环，接下来用二进制的思想进行优化。

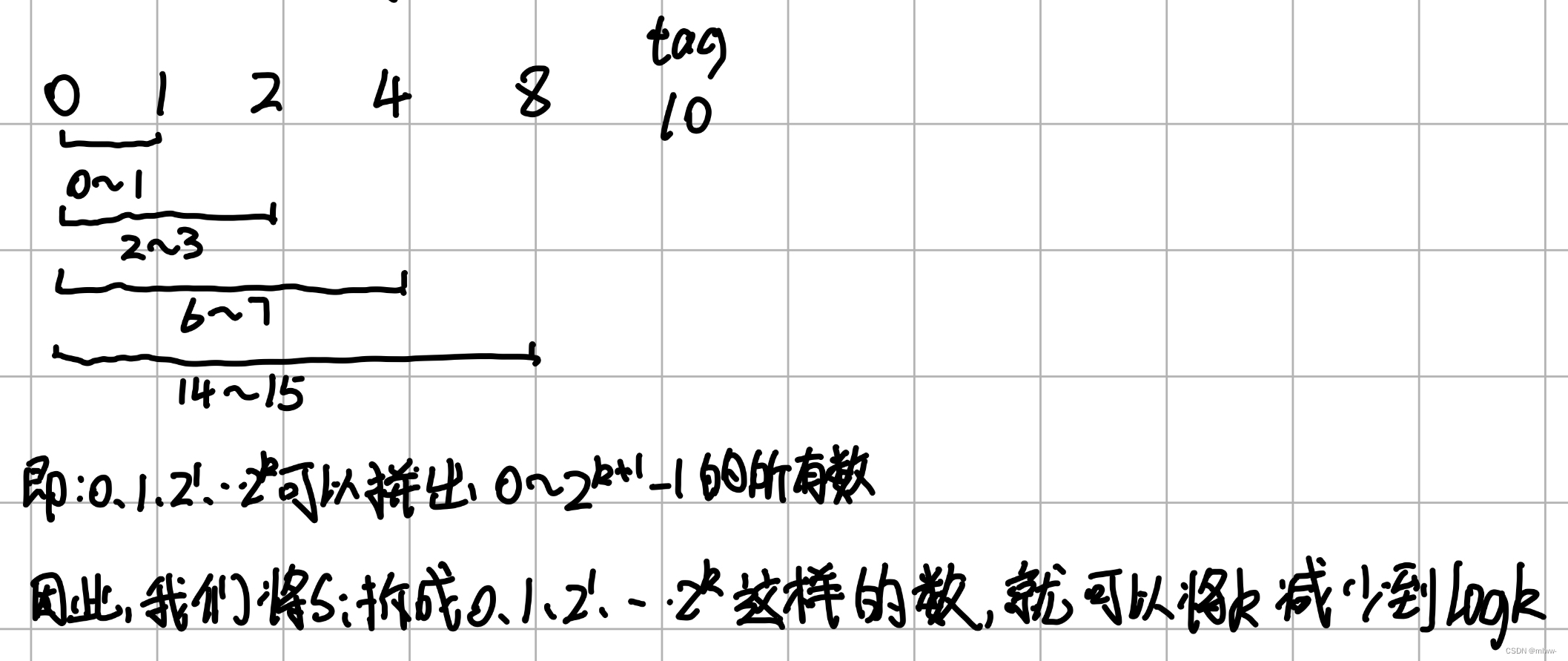
对于0~1023，我们可以通过0、1、2、4、8...512拼凑出[0,1023]区间内的所有数字。

对于0~s，我们可以通过0、1、2、4、8...2的k次方（用2k表示）、s-2k拼凑出[0,s]区间内的所有数字，其中，2k要满足：2k<s，2(k+1)>s。

#include<iostream>
using namespace std;
const int N=20010,M=2010;
int n,V;
int f[M],v[N],w[N];
int main()
{
    scanf("%d%d",&n,&V);
    int cnt=0;
    for(int i=1;i<=n;i++) 
    {
        int a,b,c;
        scanf("%d%d%d",&a,&b,&c);
        int k=1;
        while(k<=c)
        {
            cnt++;
            v[cnt]=k*a;
            w[cnt]=k*b;
            c-=k;
            k*=2;
        }
        if(c>0)
        {
            cnt++;
            v[cnt]=c*a;
            w[cnt]=c*b;
        }
    }
    for(int i=1;i<=cnt;i++)
        for(int j=V;j>=v[i];j--)
            f[j]=max(f[j],f[j-v[i]]+w[i]);
                
    printf("%d",f[V]);
}

二进制优化可以让时间复杂度下降到O(nVlogs)，接下来介绍多重背包问题的终极优化方式——用单调队列进行优化。

类比完全背包问题进行思考，我们可以列出以下式子：

f[i,j]=max(f[i-1,j-v]+w,f[i-1,j-2v]+2w,...,f[i-1,j-kv]+kw)
f[i,j-v]=max(f[i-1,j-2v]+w,f[i-1,j-3v]+2w,...,f[i-1,j-(k+1)v]+kw)
f[i,j-2v]=max(f[i-1,j-3v]+w,f[i-1,j-4v]+2w,...,f[i-1,j-(k+2)v]+kw)
......

当减到r<v时，我们会发现，f[i,r]的式子列不出来了，也就是说，我们无法利用前面的状态转移出这个状态了。

f[i,r]=?

要怎么把这个状态转移出来呢？我们转换思路，r其实是j/v的余数，我们可以用余数来表示状态，进行状态转移。

f[i,0]=max(f[i-1,v],f[i-1,2v],...,f[i-1,kv])
f[i,1]=max(f[i-1,v+1],f[i-1,2v+1],...,f[i-1,kv+1])
......
f[i,r]=max(f[i-1,v+r],f[i-1,2v+r],...,f[i-1,kv+r])

而

f[i-1,v+r]=max(f[i-1,r)+w,f[i-1,r+v])
f[i-1,2v+r]=max(f[i-1,r)+2w,f[i-1,r+v]+w,f[i-1,r+2v])
......
f[i-1,kv+r]=max(f[i-1,r)+kw,...,f[i-1,r+(k-1)v]+w,f[i-1,r+kv])

做一个变式：

f[i-1,kv+r]=max(f[i-1,r),...,f[i-1,r+(k-1)v]-(k-1)w,f[i-1,r+kv]-kw)+kw

这样就可以得到我们的状态转移方程为：

f[i,j]=f[i-1][q[hh]]+(j-q[hh])/v*w

而要求解右边的这一串max，我们可以用单调队列来做。

单调队列的步骤可以参考之前写的这篇文章：

单调栈和单调队列的模板题-CSDN博客

步骤为：

①判断队头元素是否需要出队

? ? ? ? 当队头元素的序号加上s*v后(即把所有第i种物品都放入背包)，仍然小于当前遍历到的体积，则队头元素出队。

②将所有“无用”元素出队

? ? ? ? 当队尾元素小于当前已知最大元素使，队尾元素出队

③将当前元素入队

#include<iostream>
using namespace std;
const int N=1010,M=20010;
int n,V;
int f[N][M];
int main()
{
    scanf("%d%d",&n,&V);
    for(int i=1;i<=n;i++)
    {
        int v,w,s;
        scanf("%d%d%d",&v,&w,&s);
        for(int j=0;j<v;j++)
        {
            int q[M],hh=0,tt=-1;
            for(int k=j;k<=V;k+=v)
            {
                while(tt-hh>=0&&k>q[hh]+s*v) hh++;
                while(tt-hh>=0&&f[i-1][q[tt]]+(k-q[tt])/v*w<=f[i-1][k]) tt--;
                q[++tt]=k;
                f[i][k]=f[i-1][q[hh]]+(k-q[hh])/v*w; 
            }
        }
    }
    printf("%d",f[n][V]);
}

分组背包问题

n组物品，每组物品有s种，每组只能选1种，背包体积为V。

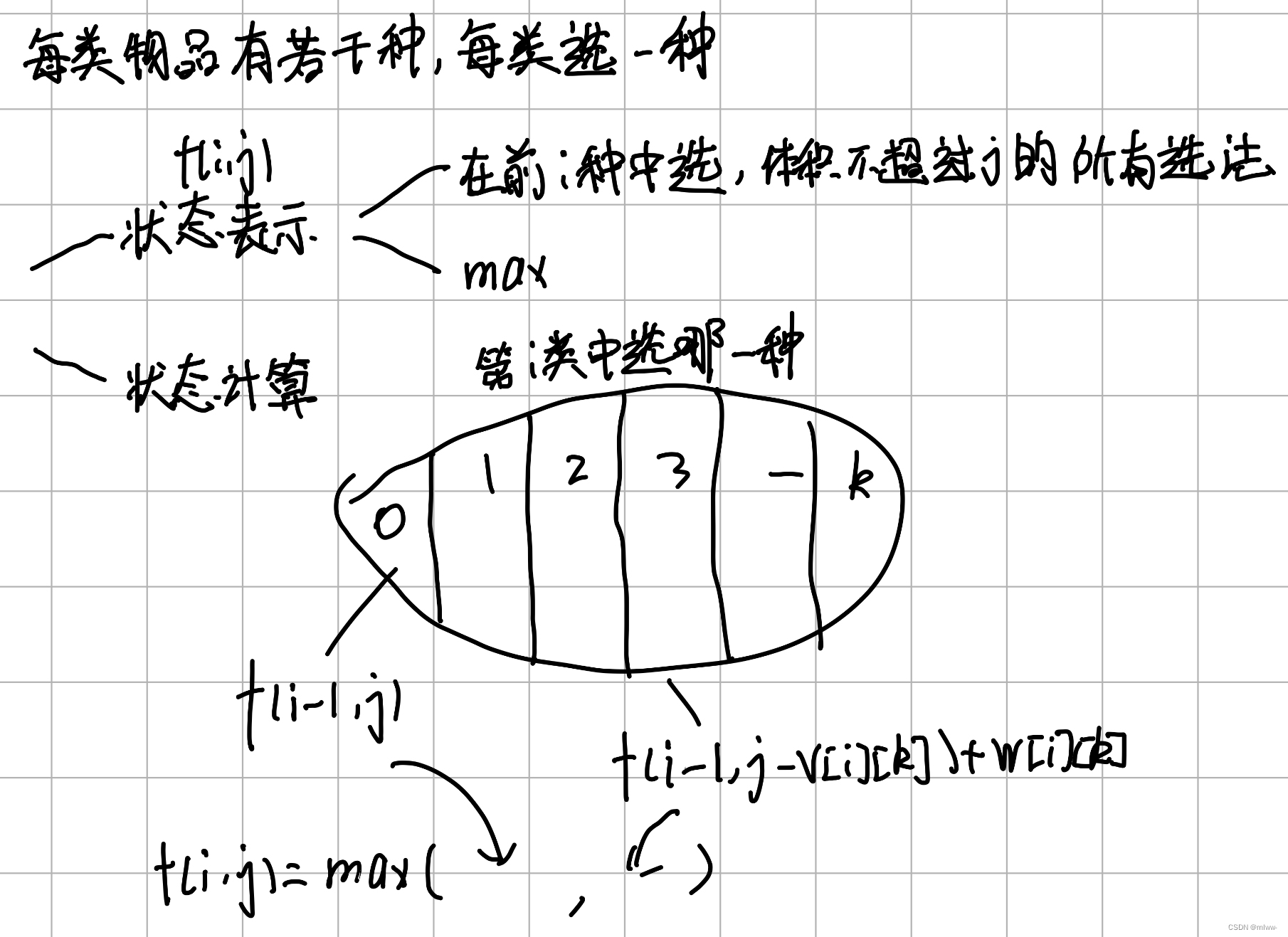
我们用是否选择了第i组物品作为状态转移的依据。将当前的状态定义为：“只在前i组物品中选，已使用体积为j”，这个状态可以由多个状态得到：“选择了第0，1，2.....s种第i组物品”。

如下图所示，可以列出状态转移方程：

#include<iostream>
using namespace std;
const int N=110;
int n,V;
int v[N][N],w[N][N],s[N];
int f[N];
int main()
{
    scanf("%d%d",&n,&V);
    for(int i=1;i<=n;i++)
    {
        scanf("%d",&s[i]);
        for(int j=1;j<=s[i];j++)
        {
            scanf("%d%d",&v[i][j],&w[i][j]);
        }
    }
    for(int i=1;i<=n;i++)
        for(int j=V;j>=1;j--)
        {
            for(int k=1;k<=s[i];k++)
            {
                if(j>=v[i][k]) f[j]=max(f[j],f[j-v[i][k]]+w[i][k]);
            }
        }
            
    printf("%d",f[V]);
}

背包问题求方案数

我们可以通过在dp过程中维护一个记录方案数的数组，完成对方案数的求解。

需要注意的是，可能存在多种方案都能得到最大结果的情况。

#include<iostream>
#include<cstring>
using namespace std;
const int N=1010,mod=1e9+7;
int n,V;
int f[N],g[N];
int main()
{
    memset(f,-1e10,sizeof(f));
    scanf("%d%d",&n,&V);
    g[0]=1;
    for(int i=1;i<=n;i++)
    {
        int v,w;
        scanf("%d%d",&v,&w);
        for(int j=V;j>=v;j--)
        {
            int t=max(f[j],f[j-v]+w);
            int s=0;
            if(t==f[j]) s+=g[j];
            if(t==f[j-v]+w) s+=g[j-v];
            if(s>=mod) s-=mod;
            g[j]=s;
            f[j]=t;
        }
    }
    int tres=0;
    for(int i=0;i<=V;i++) tres=max(tres,f[i]);
    int res=0;
    for(int i=0;i<=V;i++)
    {
        if(f[i]==tres) 
        {
            res+=g[i];
            if(res>=mod) res-=mod;
        }
    }
    printf("%d",res);
}

背包问题求方案

在进行完dp后，我们对f数组进行一个回溯的过程就好了。

#include<iostream>
using namespace std;
const int N=1010;
int n,V;
int f[N][N];
int v[N],w[N];
int main()
{
    scanf("%d%d",&n,&V);
    for(int i=1;i<=n;i++) scanf("%d%d",&v[i],&w[i]);
    for(int i=n;i>=1;i--)  
        for(int j=0;j<=V;j++)
        {
            f[i][j]=f[i+1][j];
            if(j>=v[i]) f[i][j]=max(f[i][j],f[i+1][j-v[i]]+w[i]);
        }
    int vv=V;
    for(int i=1;i<=n;i++)
    {
        if(vv>=v[i]&&f[i][vv]==f[i+1][vv-v[i]]+w[i]) 
        {
            printf("%d ",i);
            vv-=v[i];
        }
    }
    
}