java-BigDecimal

为什么浮点数 float 或 double 运算的时候会有精度丢失的风险呢？
这个和计算机保存浮点数的机制有很大关系。我们知道计算机是二进制的，而且计算机在表示一个数字时，宽度是有限的，无限循环的小数存储在计算机时，只能被截断，所以就会导致小数精度发生损失的情况。这也就是解释了为什么浮点数没有办法用二进制精确表示
BigDecimal 介绍
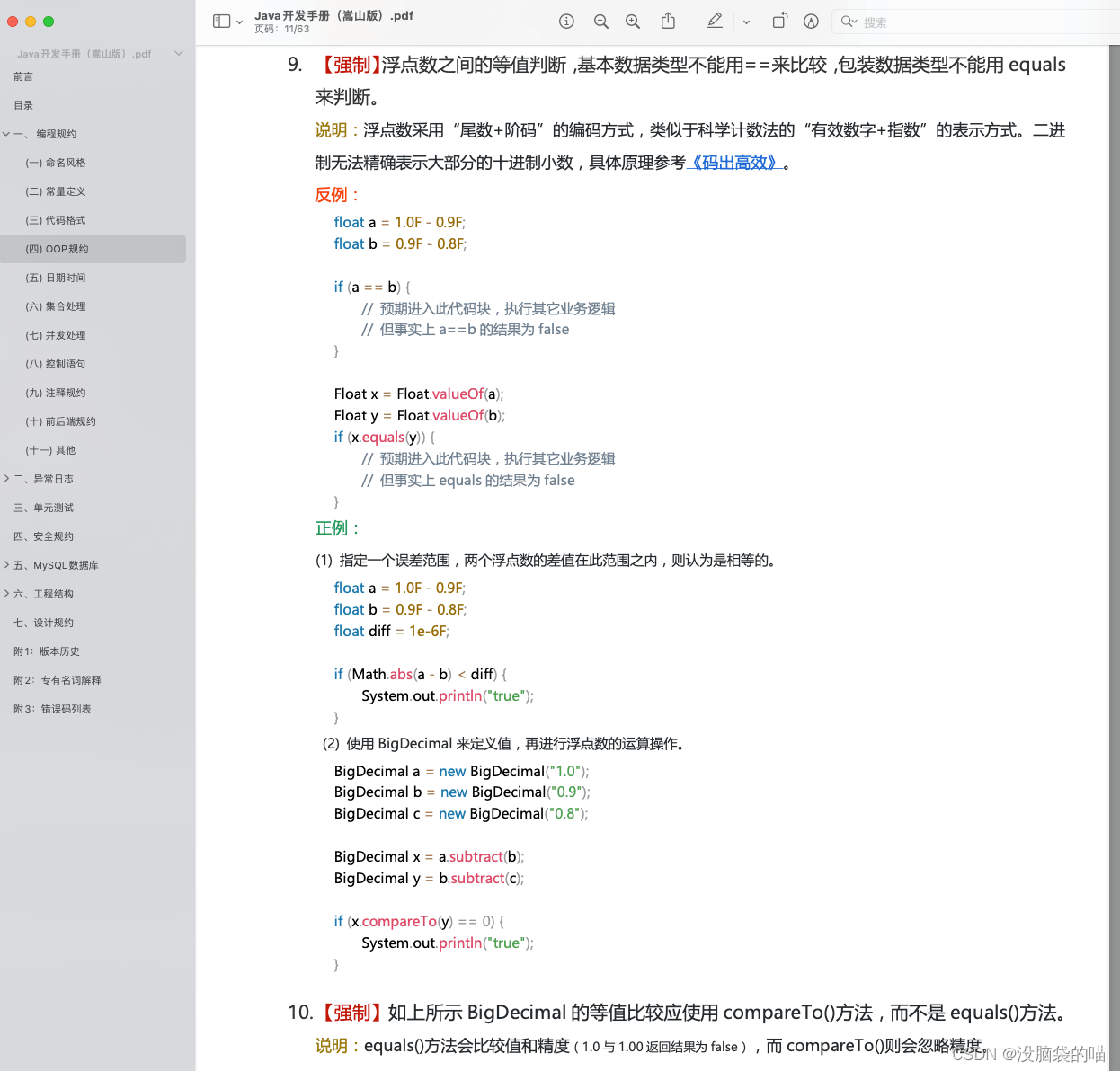
浮点数之间的等值判断，基本数据类型不能用 == 来比较，包装数据类型不能用 equals 来判断。应该使用compareTo()做判断
具体原因如下：

BigDecimal创建
!
加减乘除
add 方法用于将两个 BigDecimal 对象相加，subtract 方法用于将两个 BigDecimal 对象相减。multiply 方法用于将两个 BigDecimal 对象相乘，divide 方法用于将两个 BigDecimal 对象相除。

System.out.println(a.add(b));// 1.9
System.out.println(a.subtract(b));// 0.1
System.out.println(a.multiply(b));// 0.90
System.out.println(a.divide(b));// 无法除尽，抛出 ArithmeticException 异常
System.out.println(a.divide(b, 2, RoundingMode.HALF_UP));// 1.11

使用 divide 方法的时候尽量使用 3 个参数版本，并且RoundingMode 不要选择 UNNECESSARY，否则很可能会遇到 ArithmeticException（无法除尽出现无限循环小数的时候），其中 scale 表示要保留几位小数，roundingMode 代表保留规则。
保留规则举例
ROUND.HALF_EVEN,向最接近的偶数舍入
ROUND.HALF_UP,向最接近的整数舍入 0.5入为1
UP(BigDecimal.ROUND_UP) 向远离0的方向
// 2.5 -> 3 , 1.6 -> 2
// -1.6 -> -2 , -2.5 -> -3
DOWN(BigDecimal.ROUND_DOWN) 向接近0的方向
// 2.5 -> 2 , 1.6 -> 1
// -1.6 -> -1 , -2.5 -> -2
CEILING(BigDecimal.ROUND_CEILING),向无穷大的方向
// 2.5 -> 3 , 1.6 -> 2
// -1.6 -> -1 , -2.5 -> -2
FLOOR(BigDecimal.ROUND_FLOOR),向无穷小的方向
// 2.5 -> 2 , 1.6 -> 1
// -1.6 -> -2 , -2.5 -> -3
比较大小
a.compareTo(b) : 返回 -1 表示 a 小于 b，0 表示 a 等于 b ， 1 表示 a 大于 b。