西电期末1002.异常点检测
发布时间:2023年12月29日
一.题目

二.分析与思路
根据题目按部就班即可,不难发现西电的题目大多都是以一个简单的背景稍作嵌套命题的,主要考察基础知识点的嵌套,本题先计算平均值,再根据给出的公式计算方差,最后遍历所有数据进行判断。主要考察的点在于数据类型的选择和处理,由于开方和除法的操作,很多变量比如总数,均值,方差都使用了类型,此外,由于样本个数为整形,还涉及类型转换。
三.代码实现
#include<bits/stdc++.h>//万能头文件
int main()
{
int n;//个数为整形
scanf("%d",&n);
double num[n];//数据为双精度浮点型
double E_x=0;//期望
for(int i=0;i<n;i++){
scanf("%lf",&num[i]);
E_x+=num[i];
}//读入数据并累加到期望中
double n0=n*1.0;//隐式类型转换
E_x/=n0;//求期望
double D_x=0;//方差
for(int i=0;i<n;i++){
D_x+=(num[i]-E_x)*(num[i]-E_x);
}//累加到方差中
D_x/=(n0-1);//按照公式求出方差
double SD_x=sqrt(D_x);//按照公式的标准差
int ans=0;//用来储存答案
for(int i=0;i<n;i++){
if(num[i]<E_x-3*SD_x||num[i]>E_x+3*SD_x)ans++;
}//判断是否符合条件
printf("%.4lf %d",SD_x,ans);//打印答案,注意中间空格隔开,标准差保留4位小数
return 0;
}四.评价
其实我一开始用的不是这种方法,在概率论中方差和均值有关系的(高中数学也应该见到过):
?
推导如下:
所以代码就是:
#include<bits/stdc++.h>
int main()
{
int n;
scanf("%d",&n);
double num[n];
double E_x=0;
double E_x_square=0;
for(int i=0;i<n;i++){
scanf("%lf",&num[i]);
E_x+=num[i];//和
E_x_square+=num[i]*num[i];//平方和
}
double n0=n*1.0;
E_x/=n0;//E[X]
E_x_square/=n0;//E[X^2]
double SD_x=sqrt(E_x_square-E_x*E_x);//公式
int ans=0;
for(int i=0;i<n;i++){
if(num[i]<E_x-3*SD_x||num[i]>E_x+3*SD_x)ans++;
}
printf("%.4lf %d",SD_x,ans);
return 0;
}但是示例的运行结果不对,我百思不得其解,最后发现题目中给的方差公式分母是,把源代码计算方差的分母的
改成
,得出了和新代码一样的运行结果,我不知道是题目有一些问题还是这题目本身处理时有自己的公式,与纯数学的标准差公式有区别,但是题总归是切掉了,于是我查了一下,发现标准差其实有两种:
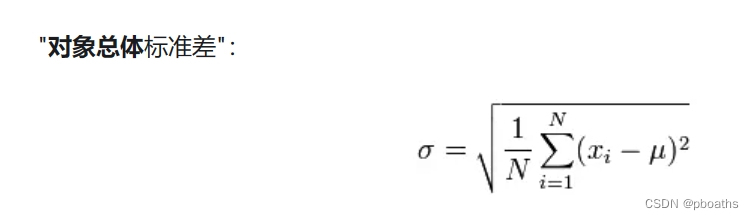
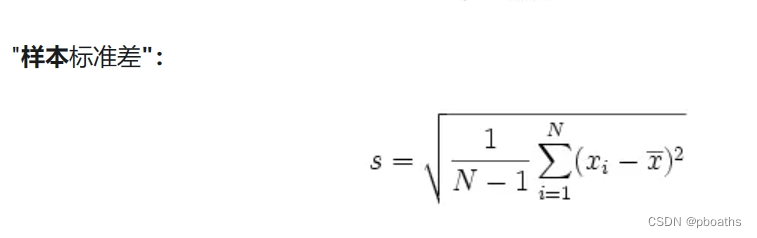
题目中叫样本标准差,我们所熟知的叫对象总体标准差,学习一下总归是好的。
文章来源:https://blog.csdn.net/pboaths/article/details/135180870
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
最新文章
- Python教程
- 深入理解 MySQL 中的 HAVING 关键字和聚合函数
- Qt之QChar编码(1)
- MyBatis入门基础篇
- 用Python脚本实现FFmpeg批量转换
- Go zero copy,复制文件
- 使用 Jamf Pro 和 Okta 工作流程实现自动化苹果设备管理
- 消失循环的2023?你都做了什么? | 2023 年度总结
- AI生成漫画或者小说推文——自动根据角色画绘本如何保持角色生成一致性的问题
- XMLParser配置
- Pandas实战100例 | 案例 51: 日期时间过滤
- 云风网(www.niech.cn)个人网站搭建(补充)HTTP常见状态码
- 基于SpringBoot+Vue校园失物招领网站的设计与实现
- Linux平台下HTTP协议使用指南与代码展示
- 微流控芯片建模分析技术与应用”专题研讨会