约束满足问题简介

发布时间：2024年01月03日

约束满足问题的定义

约束满足问题（Constraint Satisfying Problem, CSP）

– 由一个变量集合\{X_{1}-X_{n}\}和一个约束集合\{C_{1}-C_{m}\}定义；

– 每个变量都有一个非空可能值域D_{i}；

– 每个约束指定了包含若干变量的一个子集内各变量的赋值范围。

例如： 地图染色问题， N-皇后问题。

CSP问题的解

CSP的一个状态(最终解)： 对一些或全部变量的赋值 \{X_{i}=v_{i},X_{j}=v_{j},...\}

? 一个不违反任何约束的对变量的赋值称为相容赋值或合法赋值。

? 对每个变量都进行赋值称为完全赋值。

? 一个（ 一组） 对变量的赋值， 若既是相容赋值又是完全赋值(即对每个变量都赋了值，且这组赋值是合法的)， 则这个（组） 赋值是CSP问题的解。

某些CSP问题要求问题的解能使目标函数最大化——约束优化。

? CSP问题常常可以可视化， 表示为约束图， 更直观地显示问题， 帮助思考问题的答案。

CSP问题的分类

根据变量的类型划分： 离散值域和连续值域。

变量—离散值域

有限值域， 如地图染色问题， 八皇后问题。

无限值域， 如整数集合或者字符串集合。

? 例如， 对于作业规划问题， 无法枚举所有可能取值，要使用约束语言 ( 线性约束 / 非线性约束 ) 描述 ， 如StartJob_{1}+5\le{StartJob_{3}}。

变量—连续值域

最著名的连续值域CSP是线性规划问题。

– 线性规划中的约束必须是构成一个凸多边形的一组线性不等式。

– 线性规划问题可以在变量个数的多项式时间内求解。

根据约束的类型划分：

– 线性或非线性约束。

– 一元或多元约束。

? 一元约束： 只限制一个变量的取值

? 二元约束与2个变量相关

? 高阶约束： 涉及3个或更多变量。

– 通过引入辅助变量， 转为二元约束。

– 绝对约束 vs 偏好约束。

? 我们仅讨论绝对约束

CSP问题求解的复杂度

CSP问题的求解目标是找到相容的完全赋值，最朴素的想法是依次取变量的赋值组合并检查其是否满足约束条件。

– 若CSP问题的任何一个变量的最大值域为d， 那么可能的完全赋值数量为O(d^{n})。

– 指数级计算量。

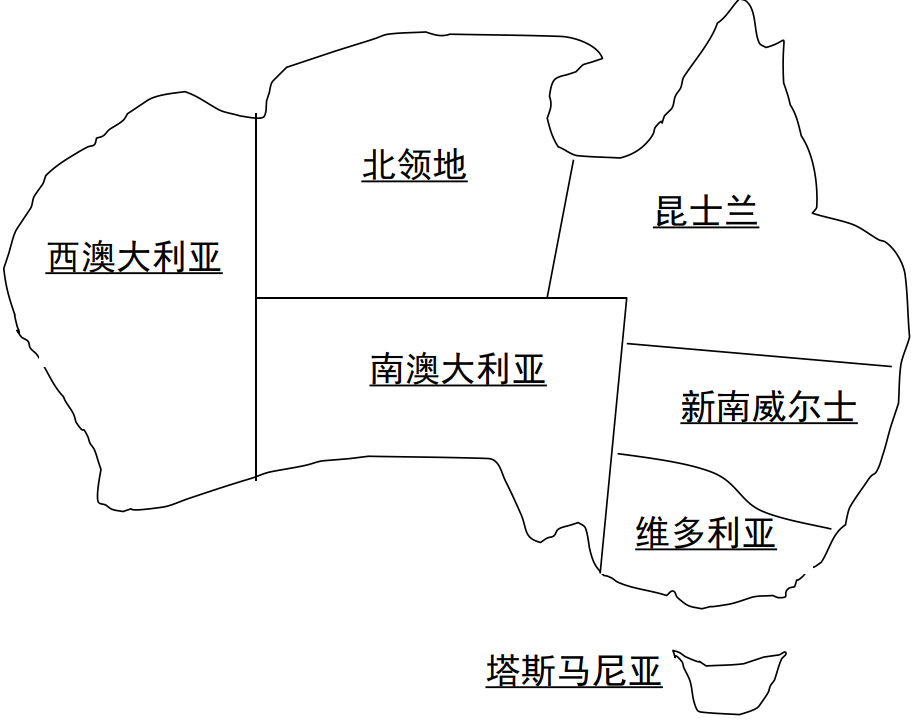
例子：澳大利亚地图染色问题

澳大利亚地图染色问题： 用红绿蓝3色标出各省， 相邻者颜色不同。

? CSP问题具有一个性质： 可交换性， 变量赋值的顺序对结果没有影响。

– 所有CSP搜索算法生成后继节点时， 在搜索树每个节点上只考虑单个变量的可能赋值。

? CSP问题的求解： 深度优先的回溯搜索。

– 每次给一个变量赋值， 当没有合法赋值(不满足约束时)就要推翻前一个变量的赋值， 重新给其赋值， 这就是回溯。

澳大利亚地图染色问题的搜索树

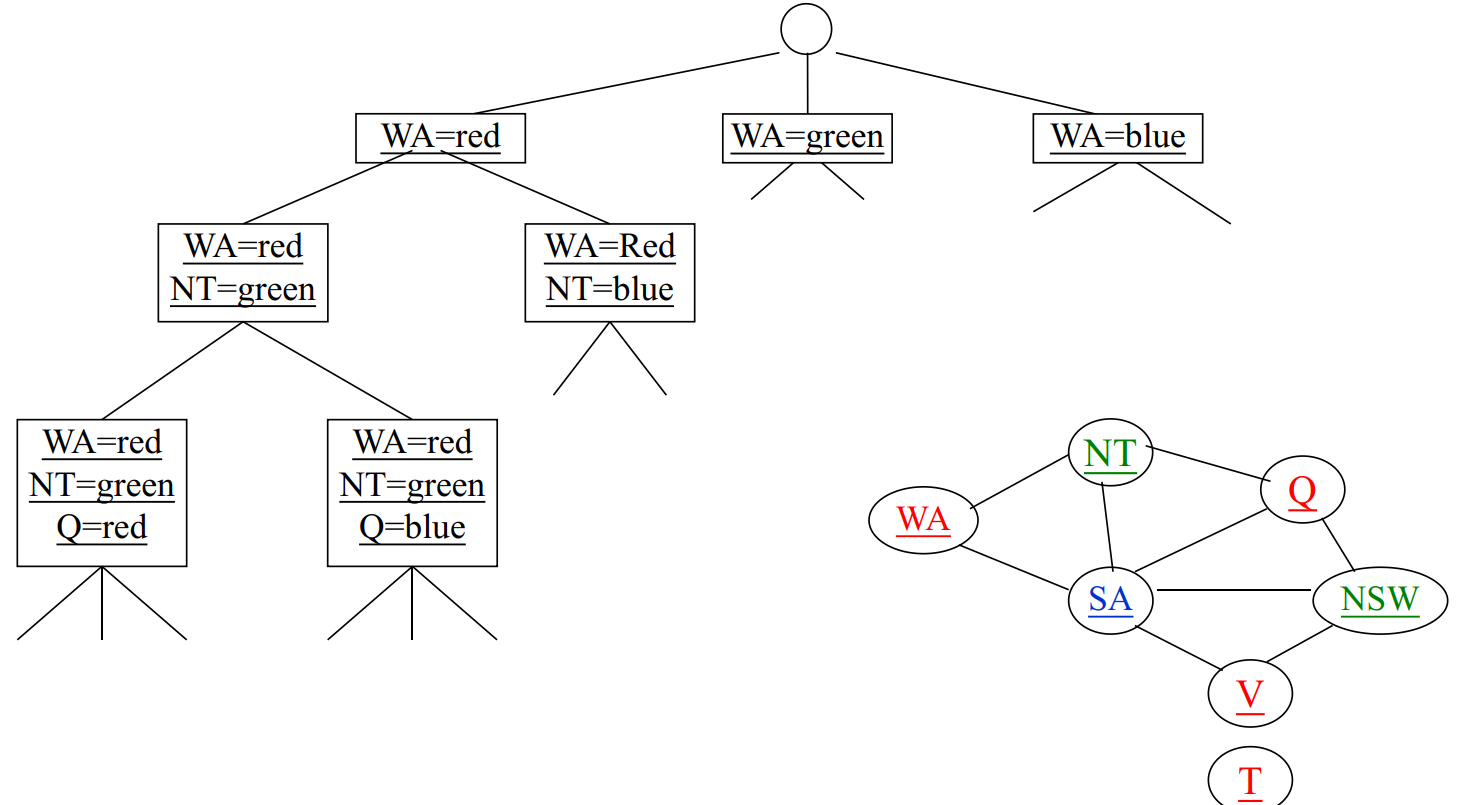
一个简单的回溯算法（深度优先)

改进思路：约束满足问题改进技术：基于变量和赋值次序的启发式-CSDN博客?

文章来源:https://blog.csdn.net/weixin_50917576/article/details/135373960
本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。
最新文章