代码随想录刷题题Day41

刷题的第四十一天，希望自己能够不断坚持下去，迎来蜕变。😀😀😀
刷题语言：C++
Day41 任务
● 583. 两个字符串的删除操作
● 72. 编辑距离
● 编辑距离总结篇

1 两个字符串的删除操作

583. 两个字符串的删除操作

思路：
动态规划
（1）确定dp数组（dp table）以及下标的含义
dp[i][j]：以i-1为结尾的字符串word1，和以j-1为结尾的字符串word2，想要达到相等，所需要删除元素的最少次数。
（2）确定递推公式

• 当word1[i - 1] 与 word2[j - 1]相同的时候
  $dp[i][j]=dp[i?1][j?1];$
• 当word1[i - 1] 与 word2[j - 1]不相同的时候
  ① 删word1[i - 1]，最少操作次数为dp[i - 1][j] + 1
  ② 删word2[j - 1]，最少操作次数为dp[i][j - 1] + 1
  ③ 同时删word1[i - 1]和word2[j - 1]，操作的最少次数为dp[i - 1][j - 1] + 2
  递推公式：$dp[i][j]=min(dp[i?1][j?1]+2,dp[i?1][j]+1,dp[i][j?1]+1);$
  （3）dp数组如何初始化

vector<vector<int>> dp(word1.size() + 1, vector<int>(word2.size() + 1));
for (int i = 0; i <= word1.size(); i++) dp[i][0] = i;
for (int j = 0; j <= word2.size(); j++) dp[0][j] = j;

（4）确定遍历顺序
从上到下，从左到右
（5）举例推导dp数组

C++：

class Solution {
public:
    int minDistance(string word1, string word2) {
        vector<vector<int>> dp(word1.size() + 1, vector<int>(word2.size() + 1));
        for (int i = 0; i <= word1.size(); i++) dp[i][0] = i;
        for (int j = 0; j <= word2.size(); j++) dp[0][j] = j;
        for (int i = 1; i <= word1.size(); i++) {
            for (int j = 1; j <= word2.size(); j++) {
                if (word1[i - 1] == word2[j - 1]) {
                    dp[i][j] = dp[i - 1][j - 1];
                } else {
                    dp[i][j] = min(dp[i - 1][j - 1] + 2, min(dp[i - 1][j] + 1, dp[i][j - 1] + 1));
                }
            }
        }
        return dp[word1.size()][word2.size()];
    }
};

时间复杂度: $O(n?m)$
空间复杂度: $O(n?m)$

2 编辑距离

72. 编辑距离

思路：
动态规划
（1）确定dp数组（dp table）以及下标的含义
dp[i][j] 表示以下标i-1为结尾的字符串word1，和以下标j-1为结尾的字符串word2，最近编辑距离为dp[i][j]
（2）确定递推公式

if (word1[i - 1] == word2[j - 1])
    //不操作
    dp[i][j] = dp[i - 1][j - 1];
if (word1[i - 1] != word2[j - 1])
    dp[i][j] = min({dp[i - 1][j - 1], dp[i - 1][j], dp[i][j - 1]}) + 1;
    

（3）dp数组如何初始化

for (int i = 0; i <= word1.size(); i++) dp[i][0] = i;
for (int j = 0; j <= word2.size(); j++) dp[0][j] = j;

（4）确定遍历顺序：从左到右从上到下去遍历

for (int i = 1; i <= word1.size(); i++) {
    for (int j = 1; j <= word2.size(); j++) {
        if (word1[i - 1] == word2[j - 1]) {
            dp[i][j] = dp[i - 1][j - 1];
        }
        else {
            dp[i][j] = min({dp[i - 1][j - 1], dp[i - 1][j], dp[i][j - 1]}) + 1;
        }
    }
}

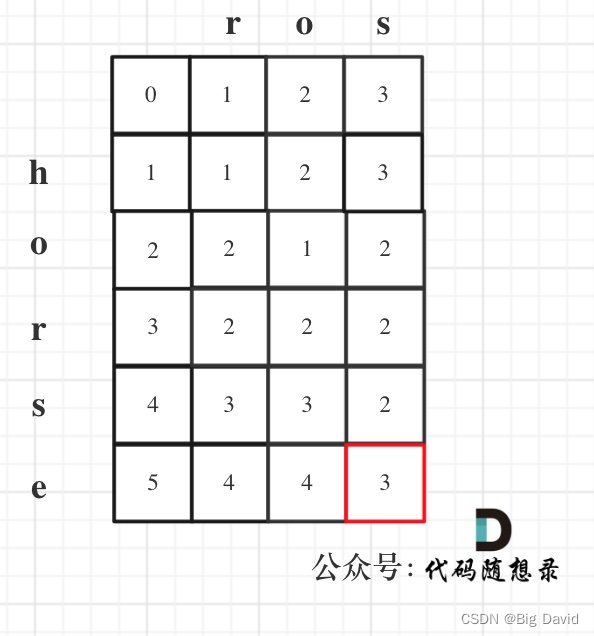
（5）举例推导dp数组

C++：

class Solution {
public:
    int minDistance(string word1, string word2) {
        vector<vector<int>> dp(word1.size() + 1, vector<int>(word2.size() + 1, 0));
        for (int i = 0; i <= word1.size(); i++) dp[i][0] = i;
        for (int j = 0; j <= word2.size(); j++) dp[0][j] = j;
        for (int i = 1; i <= word1.size(); i++) {
            for (int j = 1; j <= word2.size(); j++) {
                if (word1[i - 1] == word2[j - 1]) {
                    dp[i][j] = dp[i - 1][j - 1];
                } else {
                    dp[i][j] = min({dp[i][j - 1], dp[i - 1][j], dp[i - 1][j - 1]}) + 1;
                }
            }
        }
        return dp[word1.size()][word2.size()];
    }
};

时间复杂度: $O(n?m)$
空间复杂度: $O(n?m)$

3 动态规划之编辑距离总结

判断子序列

if (s[i - 1] == t[j - 1]) dp[i][j] = dp[i - 1][j - 1] + 1;
else dp[i][j] = dp[i][j - 1];

不同的子序列

if (s[i - 1] == t[j - 1]) {
    dp[i][j] = dp[i - 1][j - 1] + dp[i - 1][j];
} else {
    dp[i][j] = dp[i - 1][j];
}

两个字符串的删除操作

if (word1[i - 1] == word2[j - 1]) {
    dp[i][j] = dp[i - 1][j - 1];
} else {
    dp[i][j] = min({dp[i - 1][j - 1] + 2, dp[i - 1][j] + 1, dp[i][j - 1] + 1});
}

编辑距离

if (word1[i - 1] == word2[j - 1]) {
    dp[i][j] = dp[i - 1][j - 1];
}
else {
    dp[i][j] = min({dp[i - 1][j - 1], dp[i - 1][j], dp[i][j - 1]}) + 1;
}

---

鼓励坚持四十二天的自己😀😀😀