【双指针精选题目】详解8道题

讲解【双指针系列】的8道经典练习题，有三道题在另一篇博客，文末已给出链接，在讲解题目的同时给出AC代码?

目录

双指针两种类型：?

1、移动零

2、复写零

3、快乐数

4、力扣11：盛最多水的容器

5、有效三角形的个数

---

双指针两种类型：?

常?的双指针有两种形式，一种是对撞指针，一种是快慢指针。
①、对撞指针：一般用于顺序结构中，也称左右指针。
? 对撞指针从两端向中间移动。一个指针从最左端开始，另一个从最右端开始，然后逐渐往中间逼近。其终止条件一般是两个指针相遇或者错开（也可能在循环内部找到结果直接跳出循
环），也就是：

• ?left == right （两个指针指向同一个位置）
• ?left > right （两个指针错开）

②、快慢指针：又称为龟兔赛跑算法，其基本思想就是使用两个移动速度不同的指针在数组或链表等序列结构上移动。
这种方法对于处理环形链表或数组非常有用。其实不单单是环形链表或者是数组，如果我们要研究的问题出现循环往复的情况时，均可考虑使用快慢指针的思想。快慢指针的实现方式有很多种，最常用的一种就是：

• 在一次循环中,每次让慢的指针向后移动一位,而快的指针往后移动两位,实现一快一慢。

1、移动零

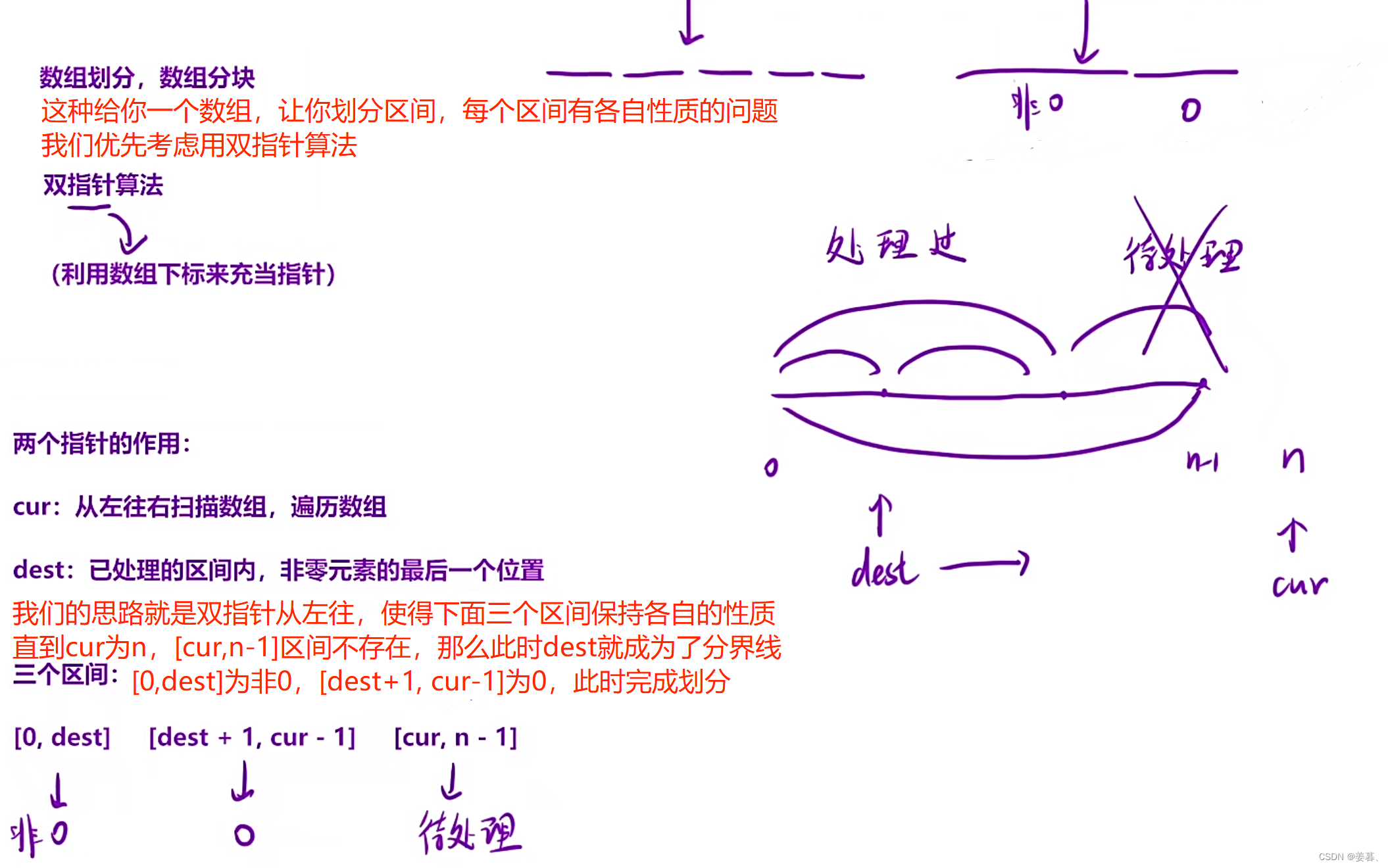
拓展知识：

这种区间划分的思路适用于快排中的最核心一步：区间划分，我们假设基准值为tmp，此时只需把区间划分为<tmp的一个区间，>tmp的一个区间和待处理区间，就能完成区间划分?

class Solution {
public:
    void moveZeroes(vector<int>& nums) {
        for (int cur = 0, dest = -1; cur < nums.size(); cur++)
            if (nums[cur])//处理非0元素
                swap(nums[++dest], nums[cur]);
    }
};

---

2、复写零

?这种在数组中移动元素，即操作数组中的元素一般我们也用双指针算法。

那么从左往右遍历不行，就试试从右往左遍历

注：上面的复写过程是假设用两个数组是为了方便演示，真正的过程是在一个数组中进行的。从上面可以知道cur一开始指向最后一个要被复写的数，即4【因为dest指向的那个数组中最后一个元素就是4，然后会从后往前遍历】，那么问题就要转化为①、找到最后一个复写的数 ②、从后往前复写

找最后一个复写的数时，cur一开始为0位置，dest一开始为-1位置

?特例处理：

注：这种半模拟半双指针的问题，一定要自己画图找出解决方案。

class Solution {
public:
    void duplicateZeros(vector<int>& arr) {
        //先找到最后一个要复写的数
        int cur = 0, dest = -1, n = arr.size();
        while (cur < n) //每次循环要先判断cur位置是否合法
        {
            //非0元素dest++，0元素dest+=2
            if (arr[cur]) dest++;
            else dest += 2;
            if (dest >= n - 1) break;//要么到了最后一个位置要么没到
            cur++;//没到cur继续往后走
        }
        //处理边界情况，判断dest是否越界
        if (dest > n - 1)
        {
            arr[n - 1] = 0;
            cur--, dest -= 2; 
        }
        //从后往前复写
        while (cur >= 0)//复写完0位置才算结束
        {
            if (arr[cur]) arr[dest--] = arr[cur--];
            else
            {
                arr[dest--] = 0;
                arr[dest--] = 0;
                cur--;
            }
        }
    }
};

---

3、快乐数

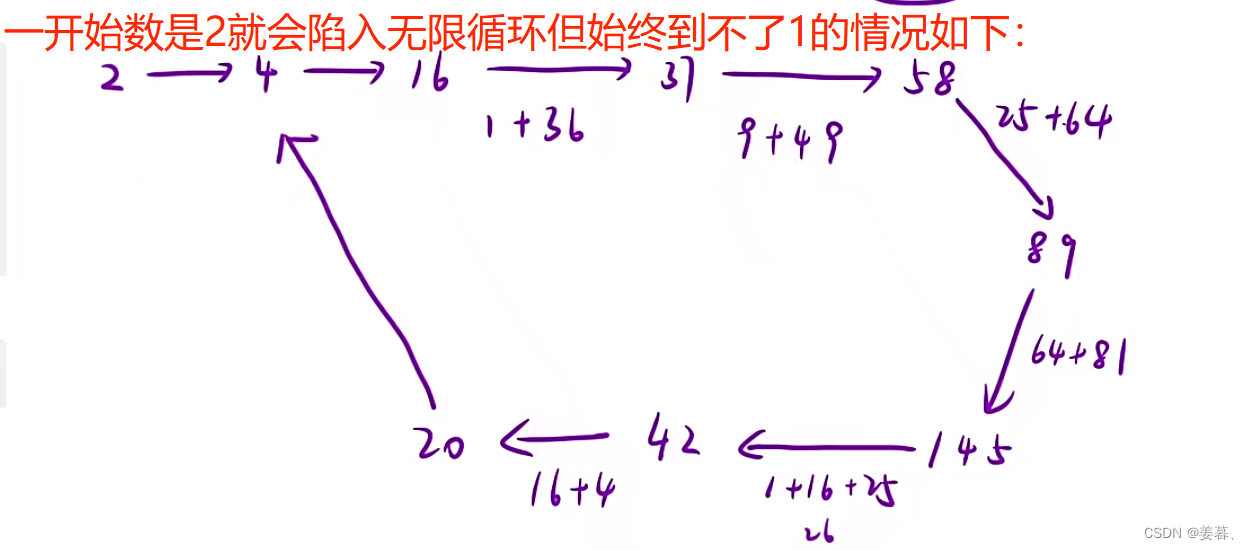
?这道题跟之前讲的环形链表题很像，建议先看我之前写过的文章：【数据结构】--单链表力扣面试题⑦环形链表-CSDN博客

证明过程可以参考【鸽巢原理】【抽屉原理】

与上面这道环形链表不同的地方在于本道题一定有环，那么代码就一点点不同罢了

class Solution {
public:
    int bitSum(int n) //返回n这个数每一位上的平方之和
    {
        int sum = 0;
        while (n)
        {
            sum += (n % 10) * (n % 10);
            n /= 10;
        }
        return sum;
    }
    bool isHappy(int n) {
        //用数来模拟快慢指针
        int slow = n, fast = bitSum(n);//slow指向第一个数，fast指向第二个数
        while (slow != fast)
        {
            slow = bitSum(slow);//slow往下走一步
            fast = bitSum(bitSum(fast));//fast往下走两步
        }
        return slow == 1;//最后一定会相遇的，因为就两种情况，直接判断==1则为true
    }
};

---

4、力扣11：盛最多水的容器

题目分析：

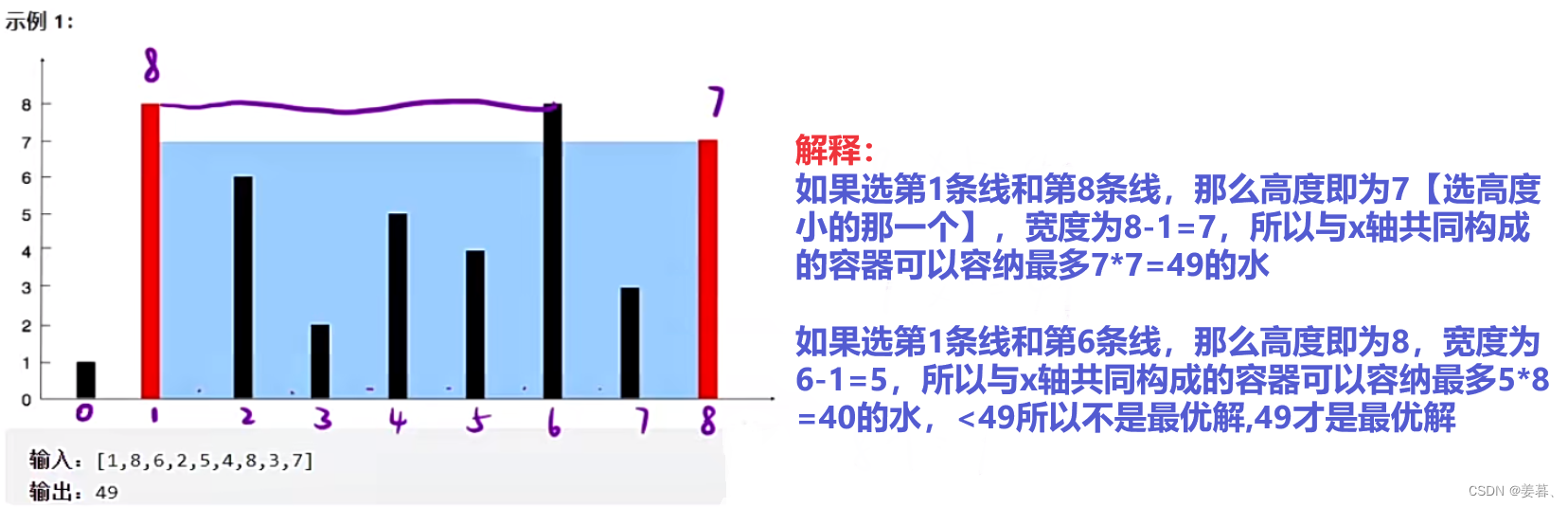
?①、暴力求解肯定能解出来，但O(n*n)肯定过不了这道题，所以要找规律优化为O(n)

class Solution {
public:
    int maxArea(vector<int>& height) {
        int left = 0, right = height.size() - 1, ret = 0;
        while (left < right)
        {
            int v = min(height[left], height[right]) *  (right - left);
            ret = max(ret, v); //求出所有v中的最大值
            //数小的指针先动
            if (height[left] < height[right]) left++; 
            else right--;
        }
        return ret;
    }
};

---

5、有效三角形的个数

三层?for 循环枚举出所有的三元组，并且判断是否能构成三?形。
虽说是暴力求解，但还是可以优化一下：
判断三?形的优化：
如果能构成三角形，需要满足任意两边之和要大于第三边。但是实际上只需让较小的两条边
之和大于第三边即可。因此我们可以先将原数组排序，然后从小到大枚举三元组，一方面省去枚举的数量，另一方面方便判断是否能构成三角形。

但下面的暴力算法会超时

class Solution {
public:
    int triangleNumber(vector<int>& nums) {
        //1、优化：先排序
        sort(nums.begin(), nums.end());

        //2、暴力解法
        int n = nums.size(), ret = 0;
        for (int i = 0; i < n; i++)
         for (int j = i + 1; j < n; j++)
            for (int k = j + 1; k < n; k++)
                if (nums[i] + nums[j] > nums[k])
                    ret++;

        return ret;
    }
};

?解法二【排序+双指针】

1、先将数组排序。
根据「解法一」中的优化思想，我们可以固定一个「最?边」，然后在比这条边小的有序数组中找出一个二元组，使这个二元组之和大于这个最?边。由于数组是有序的，我们可以利用「对撞指针」来优化。
2、设最?边枚举到?i 位置，区间 [left, right] 是i位置左边的区间（也就是比它小的区间）：
? 如果?nums[left] + nums[right] > nums[i] ：
? 说明?[left, right - 1] 区间上的所有元素均可以与?nums[right] 构成比nums[i] 大的二元组满足条件的有?right - left 种，此时?right 位置的元素的所有情况相当于全部考虑完毕， right-- ，进入下一轮判断
? 如果?nums[left] + nums[right] <= nums[i] ：
? 说明?left 位置的元素是不可能与?[left + 1, right] 位置上的元素构成满足条件
的二元组，left 位置的元素可以舍去，left++ 进入下轮循环

class Solution {
public:
    int triangleNumber(vector<int>& nums) {
        //1、优化：先排序
        sort(nums.begin(), nums.end());

        //2、双指针算法解决问题
        int n = nums.size(), ret = 0;
        //循环固定每次区间最大的数，下标最小为2，至少3个数才能判断是否为三角形
        for (int i = n - 1; i >= 2; i--)
        {
            //每固定完一个数，就进行一次循环
            int left = 0, right = i - 1;
           while (left < right)
           {
             if (nums[left] + nums[right] > nums[i]) ret += right - left, right--;
             else left++; 
           }
        }
        return ret;
    }
};

---

剩余三道题在另一篇博客：

【详解：两数之和&&三数之和&&四数之和】-CSDN博客