遗传算法解(GA)决解决旅行商(TSP)问题的python实现
旅行商(TSP)问题
旅行商问题(Traveling Salesman Problem, TSP)是组合优化领域中的一个经典问题。其基本形式可以描述为:
基本描述:一个旅行商希望访问一系列城市,每个城市仅访问一次,并最终返回出发城市。目标是找到访问所有城市的最短总路程。
输入:一组城市及它们之间的距离。
输出:一个代表城市访问顺序的路径,使得总旅行距离最短。
重要性
TSP问题在理论研究和实际应用中都非常重要。它是NP-hard问题,意味着目前没有已知的多项式时间算法能解决所有情况。
TSP问题在物流、制造、遗传学、天文学等众多领域有着广泛的应用。
解决方法
解决TSP问题的方法大致可以分为两类:精确算法和启发式算法。
精确算法:如分支界定法(Branch and Bound)、整数线性规划等。这些方法可以找到问题的确切解,但对于较大的实例,所需的计算时间可能非常长。
启发式算法:这类方法无法保证找到最优解,但在合理的时间内可以找到良好的近似解。常见的启发式算法包括:
贪婪算法(Greedy Algorithm):在每一步选择最短的可行边。
蚁群算法(Ant Colony Optimization):模拟蚂蚁觅食行为的群体智能算法。
遗传算法(Genetic Algorithm):通过模拟自然选择和遗传机制来优化路径。
模拟退火算法(Simulated Annealing):模拟物理中退火过程,通过随机搜索避免陷入局部最优。
实际应用
在实际应用中,经常会遇到TSP问题的变体,例如:
车辆路径问题(Vehicle Routing Problem, VRP):除了求最短路径外,还涉及车辆载重、客户时间窗等约束。
时间窗约束的TSP(TSP with Time Windows):访问每个城市的时间受到限制。
总的来说,TSP问题不仅在理论研究中占有重要地位,也是工业和商业应用中的常见问题。由于其NP-hard性质,寻找高效的近似解算法一直是研究的热点。
在这里我们采用遗传算法进行求解TSP问题
遗传算法
遗传算法(Genetic Algorithm, GA)是一种用于解决优化问题的启发式搜索算法,也常用于解决旅行商问题(Traveling Salesman Problem, TSP)。以下是遗传算法用于TSP问题的基本解题思路:
- 问题表示:
TSP问题通常使用城市之间的距离矩阵来表示。每个个体(解)是一种城市的访问顺序,即一个城市排列(permutation)。例如,对于N个城市,一个个体可以表示为一个包含1到N的排列,代表了访问城市的顺序。 - 初始化种群:
随机生成初始种群,其中每个个体是一个城市的排列。这个阶段的目的是为了启动算法,生成一组初始解供后续优化。 - 适应度评估:
计算每个个体(路径)的适应度,即路径的总长度。适应度越小(路径越短),个体越优秀。在TSP中,适应度就是路径的总距离。 - 选择操作:
使用选择算子(例如轮盘赌选择)按照适应度选择个体,使得适应度较好的个体有更高的概率被选中。较短路径的个体被选择的概率较大,增加了进化中优秀个体的传递概率。 - 交叉操作(交叉互换):
随机选择一对父代个体,进行交叉操作。常见的交叉操作是顺序交叉(OX)或部分映射交叉(PMX)。交叉操作产生子代个体,继承了父代个体的特征。 - 变异操作:
对子代个体进行变异操作,增加种群的多样性。在TSP中,常见的变异操作是两点变异(交换两个城市的位置)或多点变异。 - 替换操作:
将新生成的子代个体替换掉原来种群中的一部分个体。可以使用保留最优个体的策略,确保种群中至少保留当前最优解。 - 终止条件:
当达到预定的迭代次数或者算法收敛到稳定的解时,停止算法。也可以设置其他终止条件,例如连续多代没有改善时停止。通过不断地迭代选择、交叉和变异,种群中的个体将逐渐趋向于优秀的解。这样,遗传算法通过模拟自然进化的过程,从而搜索到TSP问题的较优解。在实际应用中,遗传算法的性能受到参数设置、交叉和变异操作的选择等因素影响,需要根据具体问题进行调整和优化。
代码实现
总的代码
import random
# 读取 .tsp 文件以获取元数据
def read_tsp_file(filename):
metadata = {}
with open(filename, 'r') as file:
lines = file.readlines()
for line in lines:
if line.startswith("DIMENSION"):
metadata["num_cities"] = int(line.split(":")[1])
# 可以根据需要解析其他元数据
return metadata
# 读取距离矩阵文件 .d
def read_distance_matrix(filename, num_cities):
with open(filename, 'r') as file:
lines = file.readlines()
# 解析距离矩阵
distance_matrix = []
for line in lines:
row = [int(dist) for dist in line.strip().split()]
distance_matrix.append(row)
return distance_matrix
# 计算路径长度
def calculate_path_length(path, distance_matrix):
total_distance = 0
for i in range(len(path) - 1):
total_distance += distance_matrix[path[i]][path[i + 1]]
total_distance += distance_matrix[path[-1]][path[0]] # 回到起始城市
return total_distance
# 初始化种群
def initialize_population(population_size, num_cities):
population = []
for _ in range(population_size):
individual = random.sample(range(num_cities), num_cities)
population.append(individual)
return population
# 计算适应度(路径长度)
def calculate_fitness(individual, distance_matrix):
return sum(distance_matrix[individual[i-1]][individual[i]] for i in range(len(individual)))
# 选择操作(轮盘赌算法)
def selection(population, distance_matrix):
fitness_scores = [1 / (calculate_fitness(individual, distance_matrix) + 1) for individual in population]
selected_individuals = random.choices(population, weights=fitness_scores, k=len(population))
return selected_individuals
# 交叉操作(顺序交叉)
def crossover(parent1, parent2):
start, end = sorted(random.sample(range(len(parent1)), 2))
child = [-1] * len(parent1)
for i in range(start, end + 1):
child[i] = parent1[i]
pointer = 0
for i in range(len(parent2)):
if parent2[i] not in child:
while child[pointer] != -1:
pointer = (pointer + 1) % len(parent2)
child[pointer] = parent2[i]
return child
# 变异操作(交换两个位置)
def mutate(individual):
idx1, idx2 = random.sample(range(len(individual)), 2)
individual[idx1], individual[idx2] = individual[idx2], individual[idx1]
return individual
# 遗传算法主函数
def genetic_algorithm(distance_matrix, population_size, num_generations):
num_cities = len(distance_matrix)
population = initialize_population(population_size, num_cities)
best_solution = None
best_fitness = float('inf')
for generation in range(num_generations):
# 选择
selected_population = selection(population, distance_matrix)
# 交叉
children = []
for i in range(0, population_size, 2):
child1 = crossover(selected_population[i], selected_population[i + 1])
child2 = crossover(selected_population[i + 1], selected_population[i])
children.append(child1)
children.append(child2)
# 变异
mutated_children = [mutate(child) for child in children]
# 更新种群
population = mutated_children
# 找到当前代的最优解
current_best_individual = min(population, key=lambda x: calculate_fitness(x, distance_matrix))
current_best_fitness = calculate_fitness(current_best_individual, distance_matrix)
# 如果当前代的最优解更好,更新最优解和最优适应度
if current_best_fitness < best_fitness:
best_solution = current_best_individual
best_fitness = current_best_fitness
# 打印每代的最优解
print(f"Generation {generation + 1}: Best Fitness = {current_best_fitness}")
return best_solution, best_fitness
# 主程序
if __name__ == "__main__":
population_size = 100
num_generations = 10000
'''
distance_matrix = np.array([
[0, 10, 20, 15, 30], # 城市0到其他城市的距离
[10, 0, 25, 20, 35], # 城市1到其他城市的距离
[20, 25, 0, 12, 28], # 城市2到其他城市的距离
[15, 20, 12, 0, 22], # 城市3到其他城市的距离
[30, 35, 28, 22, 0] # 城市4到其他城市的距离
])
'''
tsp_metadata = read_tsp_file("dantzig42.tsp")
distance_matrix = read_distance_matrix("dantzig42_d.txt", tsp_metadata["num_cities"])
best_path, best_distance = genetic_algorithm(distance_matrix, population_size, num_generations)
print("最短路径:", best_path)
print("最短距离:", best_distance)
结果展示
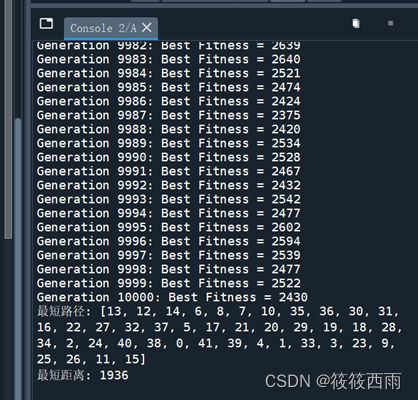
总结
遗传算法(Genetic Algorithm, GA)是一种强大的优化算法,用于解决组合优化问题,例如旅行商问题(Traveling Salesman Problem, TSP)。在处理TSP问题时,遗传算法可以产生不错的解,尤其在处理大规模问题时表现突出。在算法运行时间上:遗传算法通常能在较短的时间内找到一个相对优秀的解,尤其是与穷举法等精确算法相比。在找到的解质量上:遗传算法找到的解的质量高度依赖于算法的参数设置、种群大小、交叉率、变异率等。通过调整这些参数,可以在解的质量和算法运行时间之间寻找平衡。在局部最优解问题上:遗传算法有时可能陷入局部最优解,特别是在算法参数设置不合适或问题的搜索空间非常复杂时。为了避免陷入局部最优解,可以尝试增加种群多样性、增加变异率或者使用更复杂的选择和交叉操作。在参数调优方面:
遗传算法的性能受到参数设置的影响很大。通常需要通过实验和试错来调整参数,以获得较好的性能。种群大小的选择影响算法的全局搜索能力。较大的种群有助于增加搜索空间的覆盖度,但会增加计算开销。种群大小的选择通常需要根据问题的复杂度进行权衡。
总的来说,遗传算法在解决TSP问题上具有良好的鲁棒性和适应性。通过合适的参数设置和算法策略选择,遗传算法能够找到近似最优解,尤其在处理大规模、复杂性高的TSP实例时表现出色。
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
- Python教程
- 深入理解 MySQL 中的 HAVING 关键字和聚合函数
- Qt之QChar编码(1)
- MyBatis入门基础篇
- 用Python脚本实现FFmpeg批量转换
- EDA 数字时钟
- day01 二分查找 移除元素
- Java期末复习知识点
- 用java搞定时任务,将hashmap里面的值存到文件里面去
- Targeting S+ (version 31 and above) requires that one of FLAG_IMMUTABLE
- HashMap构造函数解析与应用场景
- 30+在线工具,实在太全了!
- 互联网上门洗鞋洗衣店小程序开发搭建;
- 2024,智能座舱不要再过度“装修”了!
- [SWPUCTF 2021 新生赛]hardrce