归并排序之C++实现
发布时间:2023年12月27日
描述
归并排序是一种经典的排序算法,采用分治的思想。
归并排序是一种基于分治思想的经典排序算法。它将待排序的数组不断地分成两个子数组,直到每个子数组只有一个元素。然后,对每个子数组进行归并排序,即不断地将两个有序的子数组合并成一个有序的数组。最终,所有子数组都合并成一个有序的数组,完成排序。
归并排序的核心操作是合并两个有序数组。合并时,从两个数组的开头依次比较元素的大小,将较小的元素放入结果数组中,直到其中一个数组的元素全部放入结果数组中。然后,将剩余的元素直接放入结果数组中,得到一个有序的合并数组。
归并排序是一种稳定的排序算法,即相等元素的相对位置在排序前后保持一致。它适用于对大规模数据进行排序,但由于递归操作和额外的空间消耗,对于小规模数据可能会有一定的性能损失。在实际应用中,可以根据数据规模和性能需求选择合适的排序算法。
实现思路
- 将待排序的数组不断地分成两个子数组,直到每个子数组只有一个元素。
- 对每个子数组进行归并排序,即不断地将两个有序的子数组合并成一个有序的数组。
- 重复上述步骤,直到所有子数组都合并成一个有序的数组。
图解
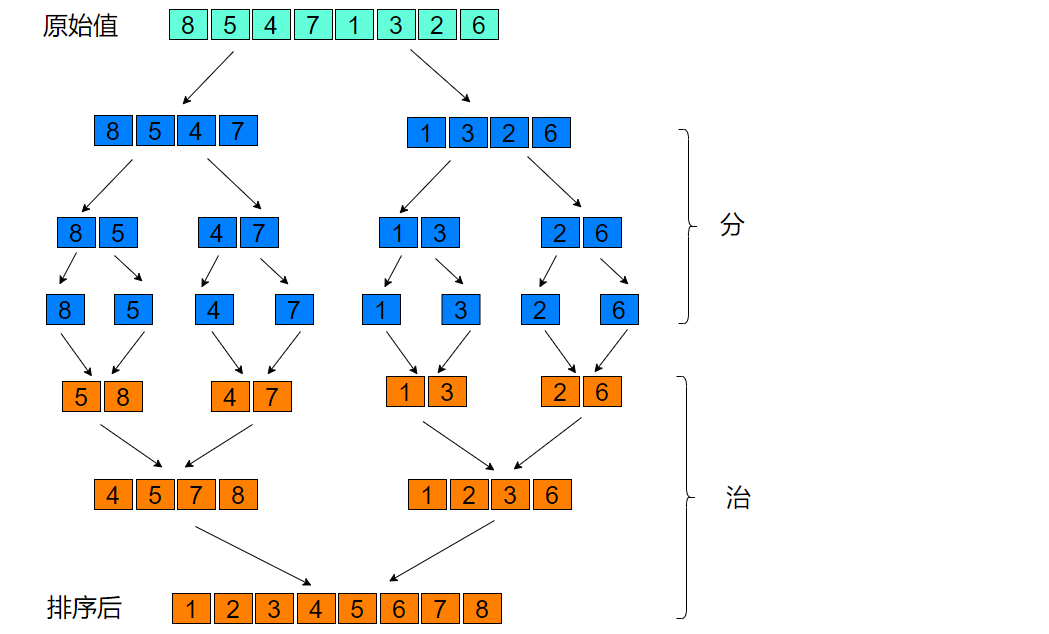
事件复杂度
归并排序的时间复杂度为O(nlogn),其中n表示待排序数组的长度。它的分治思想保证了每次都将待排序数组二分,所以排序的时间复杂度是稳定的。
空间复杂度
归并排序的空间复杂度为O(n),其中n表示待排序数组的长度。在归并排序的过程中,需要创建一个与原数组长度相同的临时数组来存放排序结果。
在归并排序的合并阶段,需要将两个子数组按照顺序合并到临时数组中。这个临时数组的长度与原数组长度相同,因为最差情况下,两个子数组的元素都要合并到临时数组中。
在递归过程中,每次将原数组分成两个子数组,然后对子数组进行排序。这样,递归的深度为logn,每层递归需要O(n)的额外空间来存放临时数组。
综上所述,归并排序的空间复杂度为O(n)。
示例
#include <iostream>
using namespace std;
// 合并两个有序数组
void merge(int arr[], int low, int mid, int high) {
int n1 = mid - low + 1; // 左半部分数组的长度
int n2 = high - mid; // 右半部分数组的长度
int leftArr[n1], rightArr[n2]; // 临时存放左右两个子数组的数组
// 将数据复制到临时数组
for (int i = 0; i < n1; i++) {
leftArr[i] = arr[low + i];
}
for (int j = 0; j < n2; j++) {
rightArr[j] = arr[mid + 1 + j];
}
// 将两个子数组合并为一个有序数组
int i = 0, j = 0, k = low;
while (i < n1 && j < n2) {
if (leftArr[i] <= rightArr[j]) {
arr[k] = leftArr[i];
i++;
} else {
arr[k] = rightArr[j];
j++;
}
k++;
}
// 将剩余的元素复制到arr中
while (i < n1) {
arr[k] = leftArr[i];
i++;
k++;
}
while (j < n2) {
arr[k] = rightArr[j];
j++;
k++;
}
}
// 归并排序
void mergeSort(int arr[], int low, int high) {
if (low < high) {
int mid = (low + high) / 2;
mergeSort(arr, low, mid); // 对左半部分数组进行排序
mergeSort(arr, mid + 1, high); // 对右半部分数组进行排序
merge(arr, low, mid, high); // 合并左右两个有序数组
}
}
int main() {
int arr[] = {5, 2, 7, 1, 3, 6, 4};
int n = sizeof(arr) / sizeof(arr[0]);
mergeSort(arr, 0, n - 1);
cout << "排序结果:";
for (int i = 0; i < n; i++) {
cout << arr[i] << " ";
}
cout << endl;
return 0;
}
注意事项
- 归并排序是稳定的排序算法,即相等元素的相对位置在排序前后保持一致。
- 归并排序的空间复杂度较高,需要额外的空间来存放临时数组。
- 在实现过程中,需要注意边界条件的处理,以避免数组越界错误。
使用技巧
- 归并排序适用于对大规模数据进行排序,因为其时间复杂度是稳定的。
- 如果待排序数组长度较小,可以使用其他简单的排序算法,如插入排序或选择排序。
结论
每天都冒出很多念头,那些不死的才叫做梦想。
文章来源:https://blog.csdn.net/MrHHHHHH/article/details/135233026
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
最新文章
- Python教程
- 深入理解 MySQL 中的 HAVING 关键字和聚合函数
- Qt之QChar编码(1)
- MyBatis入门基础篇
- 用Python脚本实现FFmpeg批量转换
- 安卓.apk的文件app应用程序开发后如何安装运行到真机上测试?
- Hive09_函数
- 一文解读Docker 网络Network
- springcloud sleuth分布式请求链路跟踪
- 如何统一给文件夹名加后缀?这个方法教你一键搞定
- 如何使用Webpack打包vue文件
- 苊,2026年市场将继续以4.2%的复合年增长率增长
- postman案例
- 旧电脑搭建NAS
- Ansible:简单、快速、安全、最强大的 IT 自动化系统 | 开源日报 No.140