图神经网络与分子表征:番外——等变术语
发布时间:2024年01月02日
本文重点参考了这篇博客:https://nb.bohrium.dp.tech/detail/1342
看论文时经常会遇到 SE3, SO3, O3 等字样,云里雾里,难以理解。本文对这些术语进行集中解释。
数学术语
在数学里,一个物体可以抽象成 3 维几何坐标。
对该物体进行旋转、平移操作,相当于,坐标矩阵乘以旋转矩阵。如下所示:
不同的操作对应不同的相乘矩阵,具体来说:
- 如果相乘矩阵是正交矩阵 O(3) ,则乘以该矩阵相当于对坐标进行一次旋转+一次镜像。(O=orthotic)
- 注意到,正交矩阵的行列式有±1之分。上述旋转对应的是正常的正交矩阵,其行列式为-1。如果正交矩阵的行列式为+1,则该矩阵被称为瑕正交矩阵,仅对坐标进行一次旋转。我们称这样的正交矩阵为 SO(3) 。(S=special)
- 在 O(3) 和 SO(3) 基础上,如果再对坐标进行平移,O 就变成了 E(E=Euclidean),该矩阵会变成 E(3) 或者 SE(3)
常见术语:
- O(3): 满足旋转、镜像等变性
- SO(3): 仅满足旋转等变性
- E(3): 满足旋转、镜像、平移等变性 (O省略没写)
- SE(3): 满足旋转,平移等变性(O省略没写)
GNN 设计要求
我们在设计 GNN 时常常要满足各种奇奇怪怪的等变要求,具体有哪些呢?
平移不变性
用户输入神经网络的几何坐标,在经过平移后,会发生变化。我们希望经过平移的坐标不对预测结果造成影响,这就是平移不变性。
满足平移不变性可以将输入坐标转换成内坐标(距离,角度,二面角等),这也是大部分不变网络设计起点。
但现在很多等变网络,通过对消息传递层进行特殊处理,使其可以满足这一要求,这使我们不拘泥于简单的不变网络。
排列、置换不变性
用户在输入分子时,不仅会输入几何坐标,还会输入每个坐标对应的元素符号。我们希望交换同种元素对应两个原子的坐标,输出结果不变/等变。
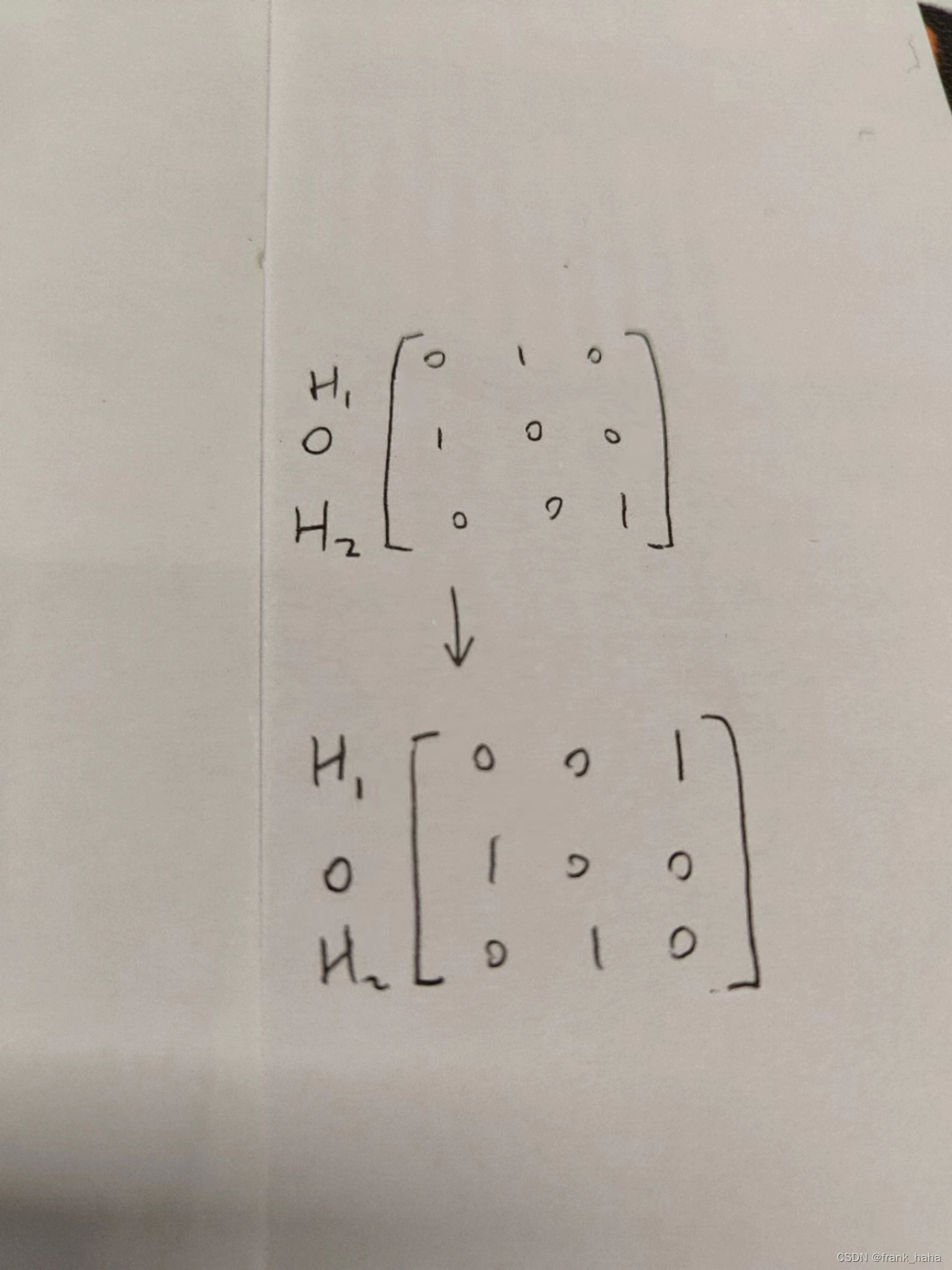
输出结果不变指,水分子能量预测等任务,水分子能量不随交换改变。
输出结果等变指,水分子中各原子受力随交换改变输出顺序。
满足排列、置换不变性要求我们的网络不能依赖于输入顺序。这条比较简单,大部分网络都满足。
镜面等变性
这个属于较为挑剔的对称性要求,对于手性分子体系可能更加重要,满足这类要求的网络通常会注明是 O(3) 或者 E(3),而不是 SO(3), SE(3)
旋转等变性
![[图片]](https://img-blog.csdnimg.cn/direct/f5ed73ea754a4ec0a6aa665480ad5beb.png)
这种情况一般出现在预测目标涉及原子受力的场景中。每个原子都有一个向量式的预测目标,这些目标会随着输入坐标的旋转而旋转,如上图所示。
这条性质是最苛刻的,满足这条性质的网络能对原子受力拟合准确度将高很多。
那么,等变性对标量性质的预测是否有帮助?
- 理论上,标量性质的预测满足不变性即可,即,上图中的第一条。
- 但是先进等变网络的设计会增加模型的表达能力,间接提高标量性质的预测能力。
- 例如,PAINN的模型设计使得模型可以鉴别出顺式、反式的分子,而这一点并不是等变性设计的本意。
- 类似的例子在LeftNet,SMP中均有提及。模型设计使其拥有更强的鉴别能力,并不代表模型具有等变性,但二者可以是同一件事情。
文章来源:https://blog.csdn.net/frank_haha/article/details/135346250
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
最新文章