C++：第十一讲DFS深搜

Everyday English

Your optimal career is simply this: Share the real you with physical world through th e process of creative self-expression.
你的最佳职业很简单，就是这样：通过创造性自我表达的途径和世界分享真实的你。

前言

今天带着大家学习一个既简单又重要的算法——深搜函数DFS。

DFS

一、基本思想

1. 为了求得问题的解，先选择某一种可能情况向前探索；
2. 在探索过程中，一旦发现原来的选择是错误的，就退回一步重新选择，继续向前探索；
3. 如此反复进行，直至得到解或证明无解

二、搜索算法

搜索算法，就是利用计算机的高性能，对问题的“状态空间”进行枚举，穷举出一个问题的全部或者部分可能的情况，找到最优解或者统计合法解的个数。 ? ? ? ?在搜索算法中，深度优先搜索算法（Depth First Search，DFS，简称深搜），常常指利用递归函数方便地实现暴力枚举的算法，也称为“回溯法”。通过递归函数，我们可以逐层地枚举每一种可能，从而实现枚举所有可能的“状态”。 ? ? ? 搜索算法是一些高级算法的基础，而搜索算法可以在很多问题中解决数据范围较小的部分。掌握正确的写搜索算法，对后续高级算法的学习和理解有着一定的帮助。

三、深搜模版（C++）

vector<int> a; // 记录每次排列 
vector<int> book; //标记是否被访问 

void DFS(int cur, int k, vector<int>& nums){
    if(cur == k){ //k个数已经选完，可以进行输出等相关操作 
        for(int i = 0; i < cur; i++){
			printf("%d ", a[i]);
		} 
        return ;
    }
    for(int i = 0; i < k; i++){ //遍历 n个数，并从中选择k个数 
        if(book[nums[i]] == 0){ //若没有被访问
            a.push_back(nums[i]); //选定本输，并加入数组 
            book[nums[i]] = 1; //标记已被访问 
            DFS(cur + 1, n, nums); //递归，cur+1 
            book[nums[i]] = 0; //释放，标记为没被访问，方便下次引用 
            a.pop_back(); //弹出刚刚标记为未访问的数
        }
    }
}

例题（洛谷P1706全排列问题）

题目描述

按照字典序输出自然数?1到?n?所有不重复的排列，即?n?的全排列，要求所产生的任一数字序列中不允许出现重复的数字。

输入格式

一个整数n。

输出格式

由1～n?组成的所有不重复的数字序列，每行一个序列。

每个数字保留?5个场宽。

输入输出样例

输入 #1

3

输出 #1

??? 1??? 2??? 3
??? 1??? 3??? 2
??? 2??? 1??? 3
??? 2??? 3??? 1
??? 3??? 1??? 2
??? 3??? 2??? 1

说明/提示

1≤n≤9。

解题思路

根据题意，对于全排列问题，以样例n=3为例，可以深度优先DFS搜索方法如图所示。

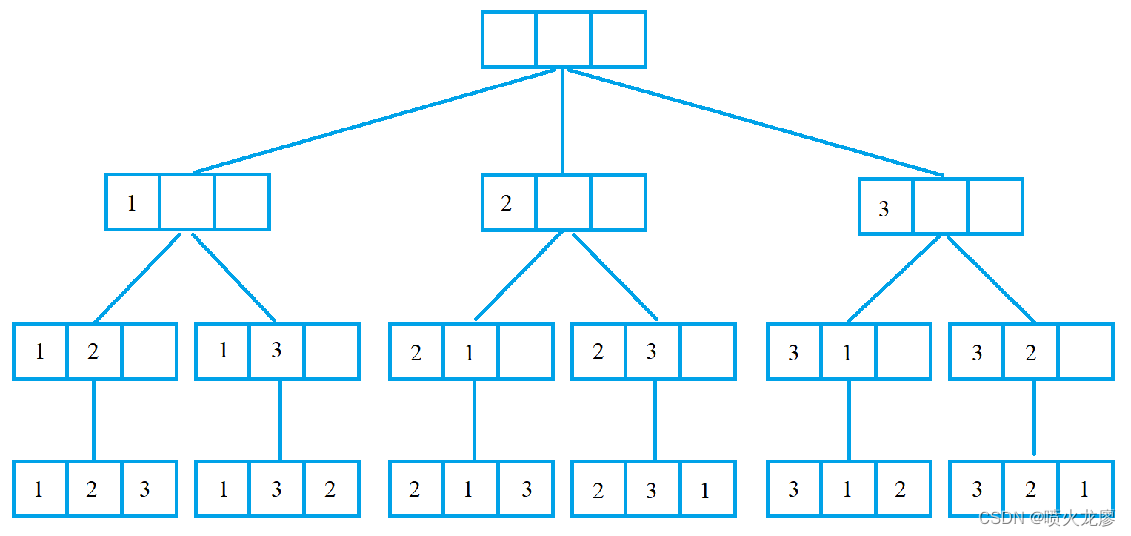
根据上述搜索过程，设计算法步骤如下：（1）用数组a保存排列，当排列的长度为n时，是一种排列方案，输出即可。（2）用数组vis记录数字是否被使用过，当vis[i]=1时，表示数字i被使用过，否则没有被使用过。 （3）DFS(u)表示已经确定了a的前u个数（从a[1]开始填数），当u>n时，输出搜索的全排列。 注意：在DFS过程中，数组vis既要标记，也要“撤销”标记。

AC?

#include<bits/stdc++.h>
using namespace std;
int a[10],n;
bool vis[10];
void dfs(int u){
	if(u>n){//当u=n+1时，表示前n个空位已填好数 
		for(int i=1;i<=n;i++){//输出一种排列方案 
			cout<<setw(5)<<a[i];
		}
		cout<<endl;
		return;//dfs的终止条件 
	}
	for(int i=1;i<=n;i++){
		if(!vis[i]){
			a[u]=i;//在第u个空位填上i 
			vis[i]=1;//标记i为已使用 
			dfs(u+1);//填下一个空位 
			vis[i]=0;//dfs回来后，要撤销之前的标记 
		}
	}
}
int main(){
	cin>>n;
	dfs(1);
	return 0;
}

setw函数

格式：
setw(……)//()内是数字
setw（）——打印格式（控制）
setw means:宽度
E.X.
setw(4):
0 ? 0 ? 0 ? 0//每个隔4格
！只适用于打印字符！

洛谷小课堂P1605 迷宫

题目描述

给定一个 N×M?方格的迷宫，迷宫里有T处障碍，障碍处不可通过。

在迷宫中移动有上下左右四种方式，每次只能移动一个方格。数据保证起点上没有障碍。

给定起点坐标和终点坐标，每个方格最多经过一次，问有多少种从起点坐标到终点坐标的方案。

输入格式

第一行为三个正整数 N,M,T，分别表示迷宫的长宽和障碍总数。

第二行为四个正整数 SX,SY,FX,FY，SX,SY?代表起点坐标,FX,FY?代表终点坐标。

接下来?T?行，每行两个正整数，表示障碍点的坐标。

输出格式

输出从起点坐标到终点坐标的方案总数。

输入输出样例:

输入 #1

2 2 1
1 1 2 2
1 2

输出 #1

1

说明/提示

对于?100%的数据，1≤N,M≤5，1≤T≤10，1≤SX,FX≤n，1≤SY,FY≤m。

解题思路

这题除了深搜，还是深搜。

深搜，一句话来总结一下，就是：

不撞南墙不回头

而在这题里，“南墙”有三个：

第一个是真墙：迷宫的围墙

也就是俗话所说的越界。越界了你还不回头，你是想去哪儿？

第二个是山墙:障碍物T

如果一障碍物横在你面前，你还是绕路吧！

第三个是人造墙：题目说了每个方格最多只能走一次

这是真没办法

所以深搜的返回条件就出来了——就是以上那三堵墙

我们每次可以从上下左右四个方向进行深搜，一旦遇上南墙就返回。

AC

#include<iostream>
using namespace std;
int n, m, t, sx, sy, fx, fy;
int  vis[10][10]; //标记
int mp[10][10]; //障碍物位置
int ans = 0;
int xx[] = { 1,0,-1,0 };
int yy[] = { 0,-1,0,1 };
void dfs(int x, int y)
{
    if (x == fx && y == fy)
    {
        ans++;
        return;
    }
    for (int i = 0; i < 4; i++)
    {
        int dx = xx[i] + x;
        int dy = yy[i] + y;
        if (dx >= 1 && dx <= n && dy >= 1 && dy <= m && vis[dx][dy]==0 && mp[dx][dy]==0)
        {
            vis[dx][dy] = 1;
            dfs(dx, dy);
            vis[dx][dy] = 0;
        }
    }
}
int main()
{
    cin >> n >> m >> t >> sx >> sy >> fx >> fy;
    while (t--)
    {
        int a, b;
        cin >> a >> b;
        mp[a][b] = 1;
    }
    vis[sx][sy] = 1;
    dfs(sx, sy);
    cout << ans << endl;
    return 0;
}

课后练习：洛谷P2404 自然数的拆分问题

题目

自然数的拆分问题 - 洛谷

解题思路

dfs递归求解，假设1到n-1每个数都有n个，现在在这n(n-1)个数里选取任意个数字，使这些数字的和为n,因此这n(n-1)个数只有选和不选两种状态，正是dfs的经典应用，得到的结果可能会有重复的

所有可以用sort和set进行排序和去重步骤

AC

#include<iostream>
#include<algorithm>
#include<vector>
#include<set>
using namespace std;
vector<int>a;
string midd;
set<string>h;
int n,t;
 
void dfs(int mid){
    if(mid==n){         //如果数的累加和等于n就记录该组合
        t++;
        vector<int>b(a);   //复制数组a
        sort(b.begin(),b.end());     //排序
        midd.clear();
        for(int i=0;i<b.size();i++){          //把整数数组转换成字符串，并存入set里去重
            midd+=(b[i]+'0');
            if(i<b.size()-1) midd+='+';
        }
        h.insert(midd);
    }
 
    for(int i=1;i<n;i++){
        if(mid+i<=n){
            mid+=i;
            a.push_back(i);
            dfs(mid);               //每一层都加入i并递归到下一层（选）
            a.pop_back();           //回溯，使得这一层不加入i（不选）
            mid-=i;
        }
    }
}
 
int main(){
    cin>>n;
    dfs(0);
    for(auto i:h)
      cout<<i<<endl;
 
    return 0;
}

结尾

本篇文章共3767字，如果你能支持一下我，我十分感谢！！！

如果你喜欢或想了解一下其他的算法，可以看看以下这些：

二分：

C++：第十讲二分查找-CSDN博客

前缀和与差分：

C++：第九讲前缀和与差分-CSDN博客

排序：

C++：第七讲冒泡排序-CSDN博客

函数：

C++第6讲max和min函数_c++ min函数-CSDN博客

C++第五讲函数初步-CSDN博客

for循环&数组：

C++第四讲for循环及数组-CSDN博客

if语句&else语句及运算：

C++第三讲：C++中的逻辑运算符及if else语句-CSDN博客

基础：

C++第二讲输入与输出-CSDN博客

C++第一讲认识C++编译器-CSDN博客

最后认识一下，我是爱编程的喷火龙廖，我们有缘再见！