频率域滤波图像复原的python实现——数字图像处理
原理
维纳滤波的原理是基于统计方法,旨在通过最小化信号的估计误差来改善信号的质量。它在处理具有噪声干扰的信号时特别有效。维纳滤波旨在从受噪声干扰的信号中恢复原始信号。它假设信号和噪声都是随机过程,并且它们的统计特性是已知的或可估计的。维纳滤波器的设计基于最小化输出和所需信号之间的均方误差(MSE)。
数学原理
假设 x(n) 是原始信号,d(n) 是观测到的受噪声干扰的信号,y(n) 是滤波器的输出。那么,噪声 v(n) 可以表示为:
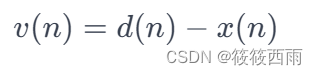
维纳滤波器的目标是找到一个滤波器 h(n),使得输出 y(n) 尽可能接近原始信号 x(n)。这可以通过最小化均方误差来实现:

在频域中,维纳滤波器的频率响应 H(f) 可以表示为:

实际应用
在实际应用中,信号和噪声的统计特性可能不完全已知,因此需要估计这些特性。维纳滤波器可以是固定的,也可以是自适应的,自适应滤波器会根据输入信号的变化动态调整其参数。维纳滤波在信号处理、图像处理、通信等领域有广泛的应用,特别是在需要从噪声中恢复信号的场合。
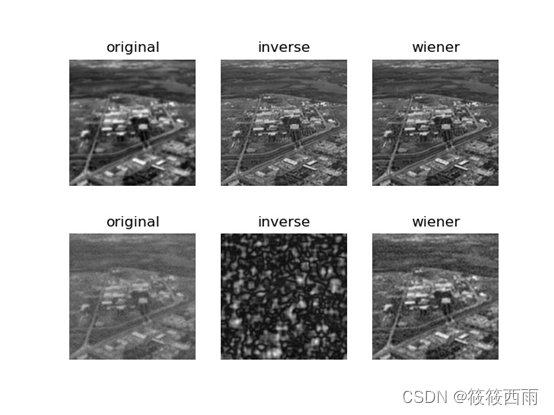
python实现下图
提示
这是一幅经过参数k=0.0025的大气湍流模型退化后的图像。结果图中的第一行是经大气湍流模型退化后的图像在逆滤波和维纳滤波后的结果:逆滤波参数和上个实验一样,限制滤波频率是通过对比值G(u,v)/H(u,v)应用一个阶数为10,截止频率为60的巴特沃斯低通函数来实现的;参数K取0.01。通过观察结果可以发现在只有退化函数作用时,逆滤波和维纳滤波的效果相差不大。结果图中第二行的基础上叠加均值为0,方差为0.01的高斯噪声形成的(可以用skimage.util.random_noise函数添加噪声),对其进行逆滤波的参数仍和上一步一样,阶数为10,截止频率为60;而维纳滤波的参数K取0.2。通过比较结果,可以看出在叠加噪声的情况下,逆滤波难以得到理想结果,而维纳滤波通过交互式地选取参数K可以较好地滤除噪声的干扰。大家可以尝试K的不同参数值,观察维纳滤波结果的表现。
python代码
import cv2
import numpy as np
import skimage
from matplotlib import pyplot as plt
img = cv2.imread('Fig0525.tif', 0)
img_n = skimage.util.random_noise(img, mode='gaussian', seed=None, clip=False, mean=0, var=0.01)
img_n = 255*(img_n-img_n.min())/(img_n.max()-img_n.min())
img_n = img_n.astype(np.uint8)
img_original_list = [img, img_n]
img_name_list = ['original', 'inverse', 'wiener']
rows = img.shape[0]
cols = img.shape[1]
Cx = rows//2
Cy = cols//2
# 大气湍流模型的参数
k = 0.0025
# 构造退化函数
H = np.zeros((rows, cols))
for x in range(rows):
for y in range(cols):
D = ((x - Cx) ** 2 + (y - Cy) ** 2) ** (5/6)
H[x, y] = np.exp(-k * D)
# 根据上一个实验得出的截止频率,构造巴特沃斯低通滤波器
D0 = 60
n = 10
HB = np.zeros((rows, cols))
for x in range(rows):
for y in range(cols):
D = np.sqrt((x-Cx)**2 + (y-Cy)**2)
HB[x, y] = 1 / (1 + (D/D0)**(2*n))
# 维纳滤波的参数
K = [0.01, 0.2]
img_inverse_list = []
img_wiener_list = []
for idx, img in enumerate(img_original_list):
dft = np.fft.fft2(img)
dft_shift = np.fft.fftshift(dft)
# 逆滤波
dft_filtered = np.multiply(np.multiply(dft_shift, 1/H), HB)
img_result = np.abs(np.fft.ifft2(np.fft.fftshift(dft_filtered)))
img_inverse_list.append(img_result)
# 维纳滤波
K_ = K[idx]
HW = np.conj(H) / ((np.abs(H) ** 2)+K_)
dft_filtered = np.multiply(dft_shift, HW)
img_result = np.abs(np.fft.ifft2(np.fft.fftshift(dft_filtered)))
img_wiener_list.append(img_result)
_, axs = plt.subplots(2, 3)
for i in range(2):
axs[i, 0].imshow(img_original_list[i], cmap='gray')
axs[i, 0].set_title(img_name_list[0])
axs[i, 0].axis('off')
axs[i, 1].imshow(img_inverse_list[i], cmap='gray')
axs[i, 1].set_title(img_name_list[1])
axs[i, 1].axis('off')
axs[i, 2].imshow(img_wiener_list[i], cmap='gray')
axs[i, 2].set_title(img_name_list[2])
axs[i, 2].axis('off')
#plt.savefig('wiener_filter.jpg')
plt.show()
结果展示

K=0.025
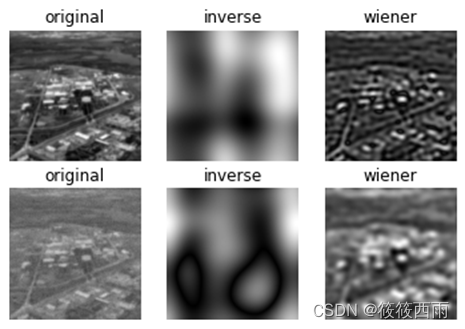
讨论
维纳滤波是美国应用数学家诺伯特·维纳(Norbert Wiener)在二十世纪四十年代提出的一种滤波器,并在1949年出版.
维纳滤波器(Wiener filter)是由数学家维纳(Norbert Wiener)提出的一种以最小平方为最优准则的线性滤波器。在一定的约束条件下,其输出与一给定函数(通常称为期望输出)的差的平方达到最小,通过数学运算最终可变为一个托布利兹方程的求解问题。维纳滤波器又被称为最小二乘滤波器或最小平方滤波器,目前是基本的滤波方法之一。维纳滤波是利用平稳随机过程的相关特性和频谱特性对混有噪声的信号进行滤波的方法,1942年美国科学家N.维纳为解决对空射击的控制问题所建立,是40年代在线性滤波理论方面所取得的最重要的成果。
维纳滤波器的优点是适应面较广,无论平稳随机过程是连续的还是离散的,是标量的还是向量的,都可应用。对某些问题,还可求出滤波器传递函数的显式解,并进而采用由简单的物理元件组成的网络构成维纳滤波器。维纳滤波器的缺点是,要求得到半无限时间区间内的全部观察数据的条件很难满足,同时它也不能用于噪声为非平稳的随机过程的情况,对于向量情况应用也不方便。因此,维纳滤波在实际问题中应用不多。实现维纳滤波的要求是:①输入过程是广义平稳的;②输入过程的统计特性是已知的。根据其他最佳准则的滤波器亦有同样要求。然而,由于输入过程取决于外界的信号、干扰环境,这种环境的统计特性常常是未知的、变化的,因而难以满足上述两个要求。这就促使人们研究自适应滤波器。
经过改变参数k,可以看出在叠加噪声的情况下,逆滤波难以得到理想结果,而维纳滤波通过交互式地选取参数K可以较好地滤除噪声的干扰。
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
- Python教程
- 深入理解 MySQL 中的 HAVING 关键字和聚合函数
- Qt之QChar编码(1)
- MyBatis入门基础篇
- 用Python脚本实现FFmpeg批量转换
- 一键优化HTML文档,轻松提升网站性能!
- 全景叙事定位 Towards Real-Time Panoptic Narrative Grounding by an End-to-End Grounding Network 论文阅读笔记
- linux的安装配置
- 【HDFS-Client】FSOutputSummer#write1方法的细节
- Golang 中的信号(Signal)机制详解
- Python 常用模块Logging
- 图形化编程:用Scratch打开趣味编程与编程思维之门
- Mysql 计算地理位置信息
- burpsuite专业版破解2023.5.21教程并配置抓包(保姆级)
- 揭秘剑南春的营业年收入157.5亿元,不单单只是数字!