具体数学复习篇——第二章和式（调和数及性质为重点）

发布时间：2023年12月27日

和式和递归式（复习时再动手算一下）——求和因子法

如果S0=a0，Sn=Sn-1+an，且an是一个n的倍数+一个常数（γn+β），则可转化为：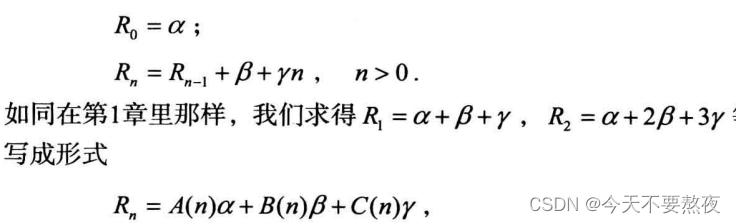

?这里令Rn分别为1，n和n方，计算得出A(n)B(n)和C(n)

这里想要计算a+bk的和式，找到对应的R0为a即α，an为a+bn，则β为a，γ为b?

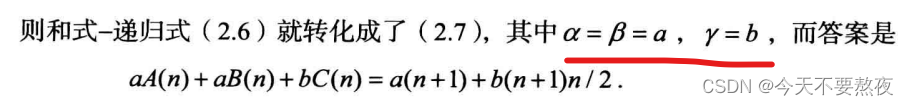
此外对于形如

利用公式可以得到

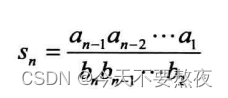
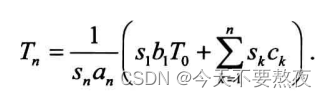
例如下式中an=n，bn=n+1，cn=2n

这里需要注意的是分界点n>2（书上P39）

调和数及性质

证明如下等式（必须掌握）

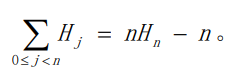
要通过一个多重和式来计算

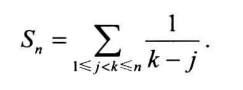
如果要证明的式子左边是j，那么求和顺序为先求k再求j于是最后就会出现j的形式（对谁求和就替换谁）

若先求的是j

这样就搞出了等式的左边，那么等式的右边就需要：?

同理或者可以先用k-j替换j，然后先求和k

扰动法（加一个尾再甩出一个头）

对于例子：

利用扰动法可以解决：

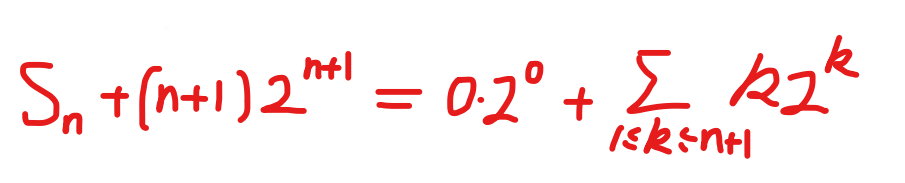
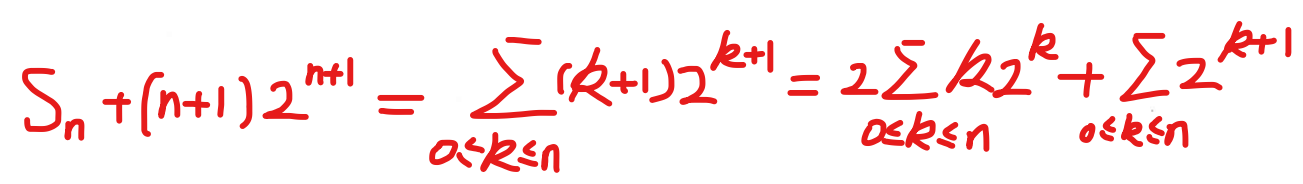
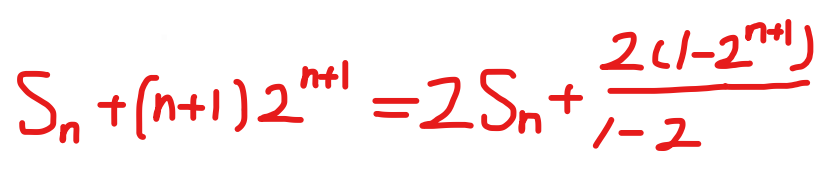
差分算子，上升和下降阶乘幂和差分法求解

差分算子△

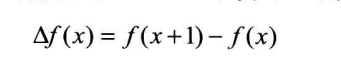
下降阶乘幂

上升阶乘幂

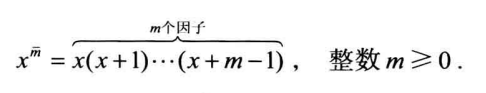
必须掌握（特别注意这里是x+1的下降阶次幂）

微分对应差分，积分对应离散求和?

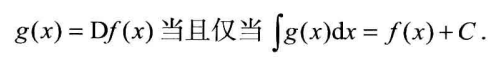
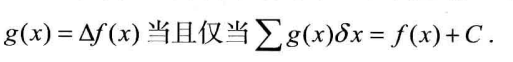
注意其上下界限

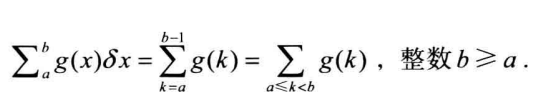
例子：

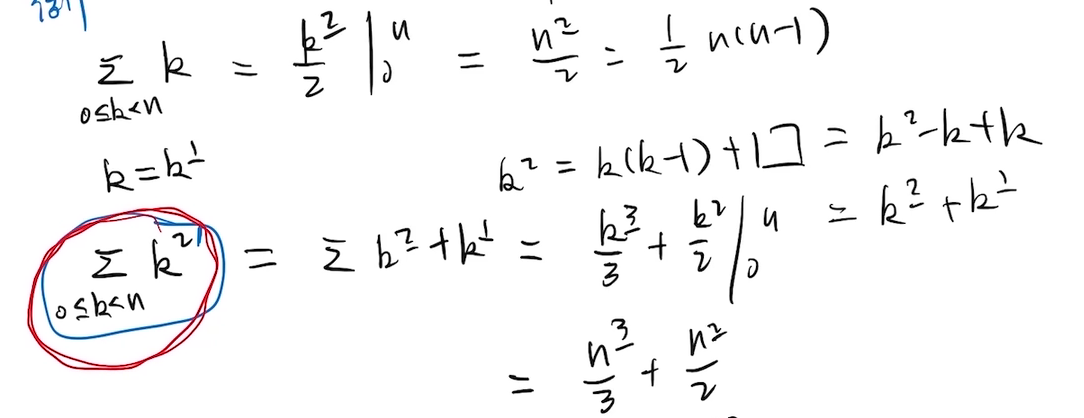
但是遇到正常的幂次需要转换为阶乘幂

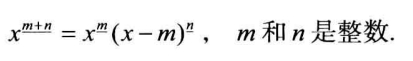
差分法求解和式（即利用分部求和法则） 重点！

?

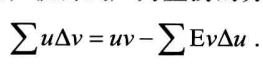
?重点：

?

?

文章来源:https://blog.csdn.net/remaining2/article/details/135208530
本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。
最新文章