Java版的XIRR(内部收益率)实现

01 为什么要使用XIRR？

? ? ? ? 采用新的函数往往是因为旧的函数无法满足现有需求；那么旧的函数是什么呢？（IRR）

IRR就是现金流入现值总额与现金流出现值总额相等、净现值等于零时的折现率。

IRR的计算只能用来计算定期现金流的内部收益率，例如每月定投、每年奖金等，面对不定期的情况则无能为力。

02 什么是XIRR函数？

XIRR 函数用来基于指定的一系列可能不规则分布的现金流，计算投资的内部收益率。

03 XIRR计算公式

其中：

1、 di = 第i个支付日期

2、d1 = 第0个支付日期

3、pi = 第i个或最后一个支付金额

4、rate就是我们要计算的XIRR

与IRR相比，区别在于1+rate的幂次方，Xirr的幂次方为当前现金流与初试现金流的天数差与一年天数的百分比；

04 如何使用java代码计算出rate结果？

? ? ? ? 首先在编写代码之前我们要回顾回顾一些基本的数学知识。

1、如何求解？

面对这种复杂的方程求解通常会采用牛顿迭代法进行求解；

2、牛顿迭代法的基本思路：

? ? ? ? a：先猜测一个初始值X0；

? ? ? ? b：在函数f（x）上找到点（X0，f(X0)）处的切线；

? ? ? ? c：切线与X轴的焦点作为新的猜测值X1；

? ? ? ? d：重复步骤b、c，直到满足所需的精度或达到最大迭代次数。

当y=0时：

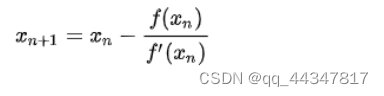
05 XIRR核心代码计算详解：

参数：

newTonsXirr Xirr：计算流水 对象属性包含 资金流水以及时间流水；

guess ：猜想值

tries：尝试次数

err：精度

public double xirr(NewtonsXirr newtonsXirr, double guess) {
double x0 = guess;
double err = 1e+100;
// 牛顿迭代法最大次数循环尝试求取结果
for (int i = 0; err > precision; i++) {

// 超出最大迭代次数退出循环
if (i >= tries) {
String message = MessageFormat.format("Not accurate enough after {0} tries, rate: {1}, error: {2}", i, x0, err);
throw new XirrException(message, x0, err);
}

// 获取下一次猜想值
double x1 = next(x0);

// 精度计算
err = Math.abs(x1 - x0);
x0 = x1;
}
return x0;
}

// 获取下一次猜想值

public double next(double x) {
double fr = 0.0;
double dfr = 0.0;
double r = 1.0 + x;
for (int i = 0; i < values.length; i++) {

//负的?(di-d0)/365
double p = (days[0] - days[i]) / 365.0;

// Pi*(1+rate)^p? 负次方等于倒数
fr += values[i] * Math.pow(r, p);

// f(x)=x^n? 幂函数导数：f(x)' = nx^(n-1)
dfr += p * values[i] * Math.pow(r, p - 1.0);
}

// 牛顿迭代法：x = x-f(x)/f(x)'
return x - fr / dfr;
}

06 引用源码地址：https://github.com/joutvhu/xirr

欢迎大家留言讨论