1.11寒假集训

A:

解题思路：

这题看示例不难发现，答案就是a * b的每一项的和，例如111 111就是111*（1 + 1 + 1）= 333,知道后此题就迎刃而解了

下面是c++代码：

#include<iostream>
using namespace std;
int main()
{
    int t;
    long long a,b;
    cin >> t;
    while(t != 0){
        int sum = 0;
        cin >> a >> b;
        while(b != 0){
            sum += b % 10;
            b = b / 10;
        }
        cout << a * sum << endl;
        t--;
    }
    return 0;
}

B:

解题思路：

这题就是判断一个数每截取掉最后一位是是否都为素数，判断素数很简单，但是要注意数量级，10e4和10e6,如果直接判断的话肯定会超时，所以只需要判断到该数的平方分根即可，当判断某个数不为素数时，那就不需要判断其他的右截断数了，减少程序运行时间。

下面是c++代码：

#include<iostream>
#include<cmath>
using namespace std;
int main()
{
    int T,A;
    cin >> T;
    while(T != 0){
        cin >> A;
        int num = 1;
        while(A != 0){
            int sum = A;
            if(sum == 1){
                num = 0;
            }
            for(int i = 2;i <= sqrt(sum);i++){
                if(sum % i == 0){
                    num = 0;
                    break;
                }
            }
            if(num == 0){
                break;
            }
            A /= 10;
        }
        if(num == 1){
            cout << "YES" << endl;
        }else{
            cout << "NO" << endl;
        }
        T--;
    }
    return 0;
}

C:

解题思路：

这道题直接判断x + i * (y - x) / i * 1.0 == y是否为真，化成double型是因为如果能整除就相等，不能整除就为假，找到后直接break。

下面是c++代码：

#include<iostream>
using namespace std;
int main()
{
    int t,x,y,a,b;
    cin >> t;
    while(t != 0){
        cin >> x >> y;
        if(x >= y){
            cout << -1 << " " << -1 << endl;
        }
        for(double i = 1;i <= y - x;i++){
            if(x + i * (y - x) / i * 1.0 == y){
                cout << i << " " << (y - x) / i << endl;
                break;
            }
        }
        t--;
    }
    return 0;
}

D:

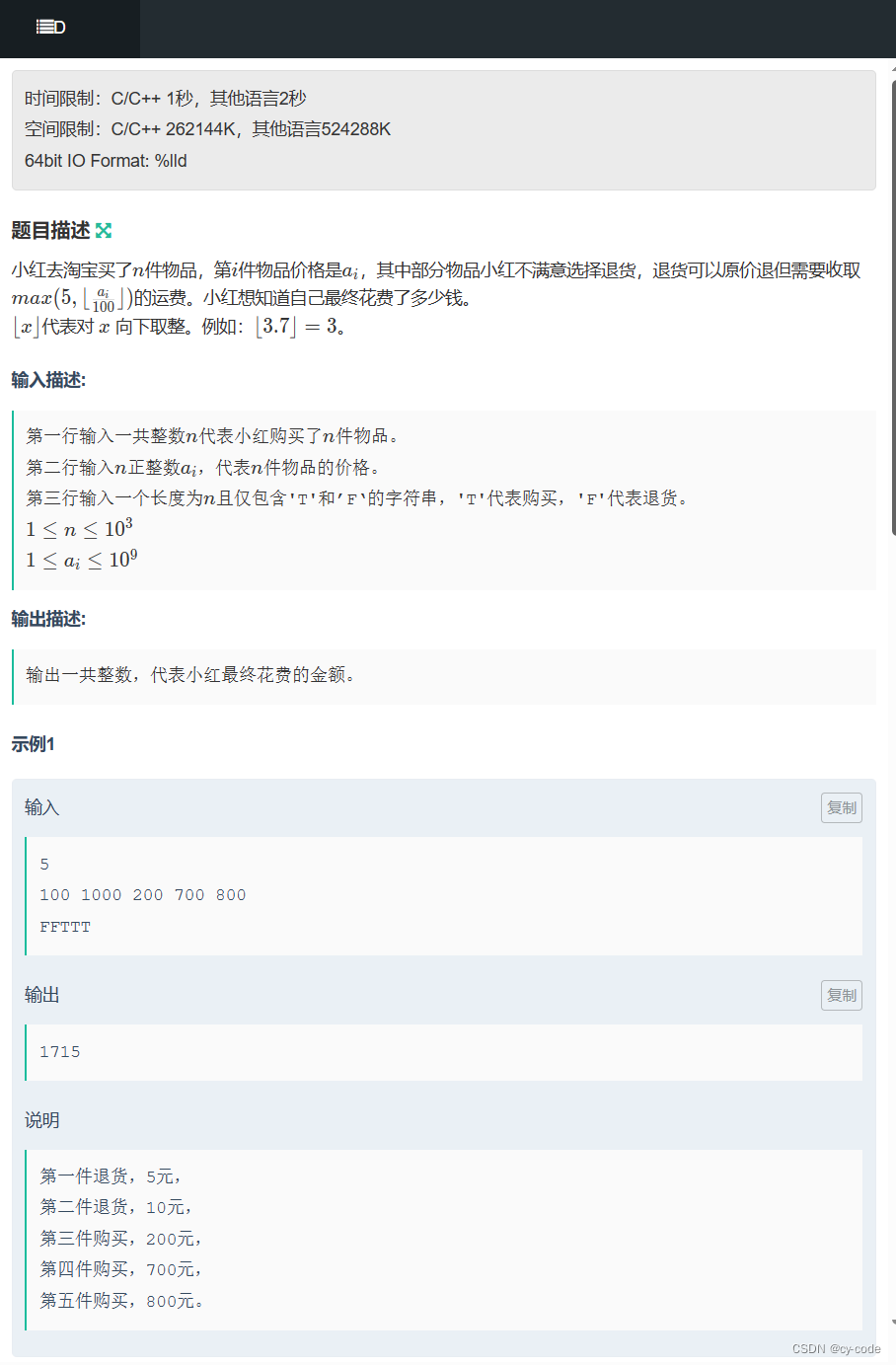
解题思路：

向下取整用到<cmath>库中的floor()函数，遍历数组和字符串，应为是一一对应的，所以就一起遍历，如果字符为'F',就判断arr[i] / 100向下取整和5谁大，就加上谁，如果为'T'，就加上衣服价格，最后输出即可。

下面是c++代码：

#include<iostream>
#include<cmath>
using namespace std;
int main()
{
    int n, arr[1000];
    long long num = 0;
    string s;
    cin >> n;
    for (int i = 0; i < n; i++) {
        cin >> arr[i];
    }
    cin >> s;
    for (int i = 0; i < n; i++) {
        if (s[i] == 'F') {
            if (floor(arr[i] / 100) > 5) {
                num += floor(arr[i] / 100);
            }
            else {
                num += 5;
            }
        }
        else {
            num += arr[i];
        }
    }
    cout << num;
    return 0;
}

E:

解题思路：

这道题卡了我好久，三种情况

(1).当m >= x时，输出x

(2).当x % m == 0s时，输出m

(3).输出x - (x / m) * m

下面是c++代码：

#include<iostream>
using namespace std;
int main()
{
    unsigned long long n,m,x;
    cin >> n;
    for(int i = 0;i < n;i++){
        cin >> m >> x;
        if(m >= x){
            cout << x << endl;
        }else if(x % m == 0){
            cout << m << endl;
        }else{
            cout << x - (x / m) * m << endl;
        }
    }
    return 0;
}