2023-12-23 组合总和 III和电话号码的字母组合
发布时间:2023年12月28日
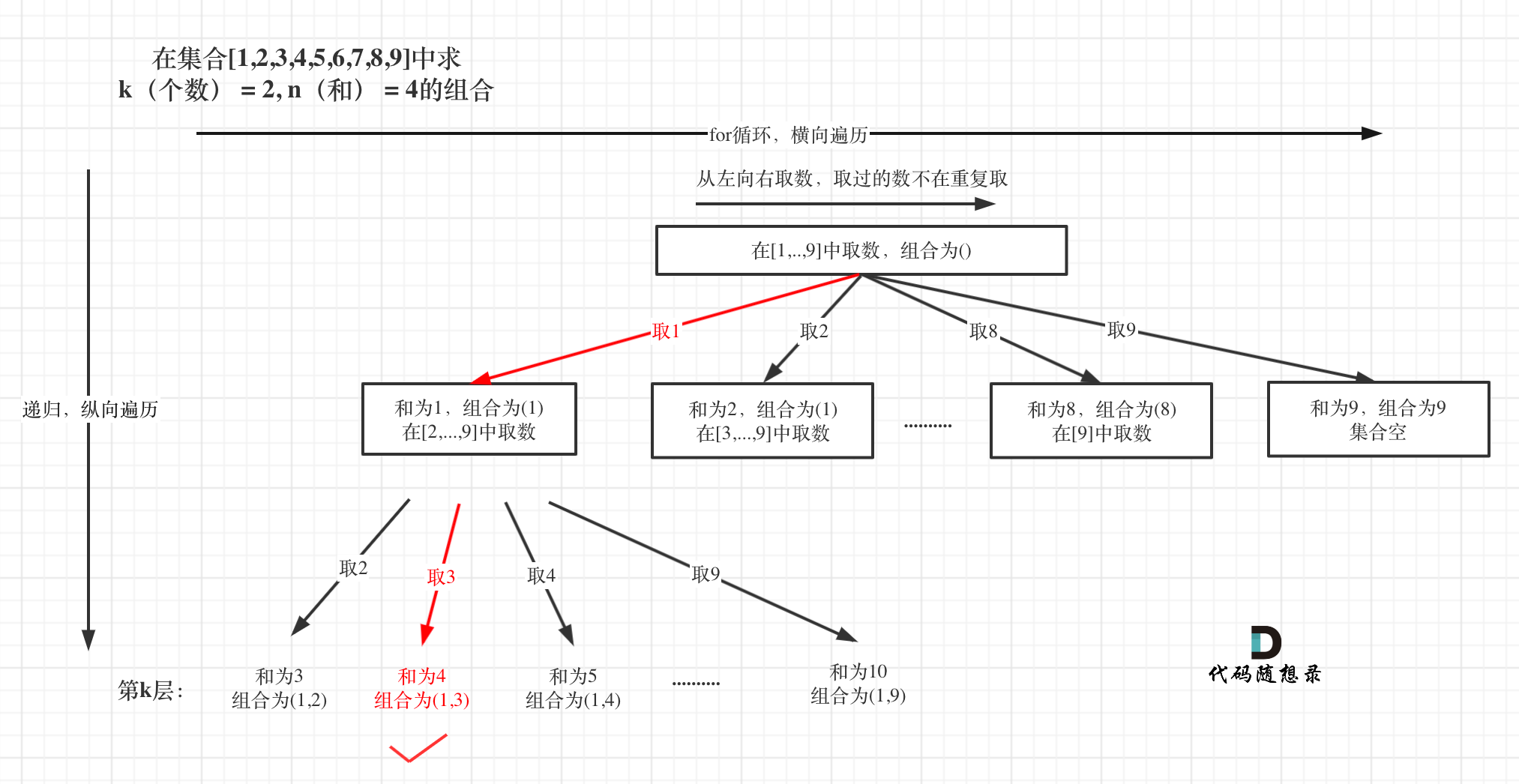
216. 组合总和 III

思路:使用回溯三部曲!① 确认需要传入的参数以及返回值 ② 回溯的终止条件 ③ 单层搜索的逻辑!这道题易错点在于单层的逻辑上的遍历起始位置以及回溯回退步骤里要执行的内容!
class Solution:
def combinationSum3(self, k: int, n: int) -> List[List[int]]:
result = []
self.backtrack(k, n, 1,[], 0, result)
return result
# 回溯三部曲
# 传入参数以及返回值
def backtrack(self, k, n, start,temp_res,target, result):
# 回溯条件
if k == 0:
if target == n:
# 使用切片
result.append(temp_res[:])
return
# 单层搜索过程
for i in range(start, 10):
# 剪枝操作
if target > n:
continue
temp_res.append(i)
target += i
# self.backtrack(k - 1, n, start + 1, temp_res, target, result)
# 这里应该是i + 1的而不是start + 1
self.backtrack(k - 1, n, i + 1, temp_res, target, result)
temp_res.pop()
# target也需要回退
target -= i
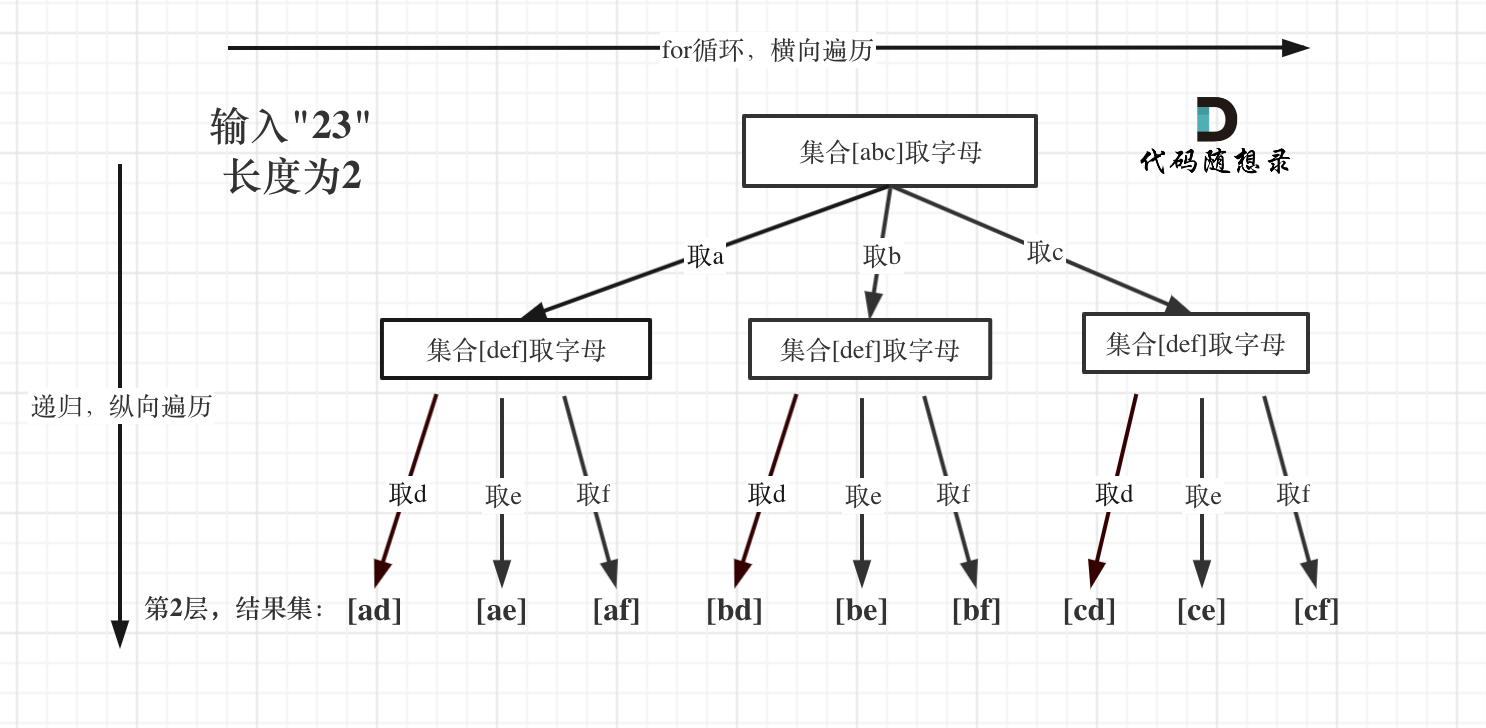
17. 电话号码的字母组合

核心:依旧是回溯三部曲!有个点需要注意的是"".join(res),如果res是空的话,那么最终内容会是这样的[ “” ]而不是[ ]这样了!还不需要进行剪枝
class Solution:
def letterCombinations(self, digits: str) -> List[str]:
dict_ziwu = {"2":['a','b','c'],"3":["d","e","f"],"4":["g","h","i"],
"5":["j","k","l"],"6":["m","n","o"],"7":["p","q","r","s"],"8":["t","u","v"],"9":["w","x","y","z"]}
length = len(digits)
result = []
# if digits == "":
# return result
self.backtrack(digits,0,length,[],result,dict_ziwu)
return result
# 回溯参数
def backtrack(self, str1, start, length, res, result,dict_ziwu):
# 回溯 终止条件
if start == length:
if res:
result.append("".join(res))
return
list_temp = dict_ziwu[str1[start]]
# 回溯单层搜索逻辑
for _list in list_temp:
res.append(_list)
start += 1
self.backtrack(str1,start,length,res,result,dict_ziwu)
res.pop()
start -= 1
# 优化版本
class Solution:
def __init__(self):
self.letterMap = [
"", # 0
"", # 1
"abc", # 2
"def", # 3
"ghi", # 4
"jkl", # 5
"mno", # 6
"pqrs", # 7
"tuv", # 8
"wxyz" # 9
]
self.result = []
self.s = ""
def backtracking(self, digits, index):
if index == len(digits):
self.result.append(self.s)
return
digit = int(digits[index]) # 将索引处的数字转换为整数!注意这里别弄混了!
letters = self.letterMap[digit] # 获取对应的字符集
for i in range(len(letters)):
self.s += letters[i] # 处理字符
self.backtracking(digits, index + 1) # 递归调用,注意索引加1,处理下一个数字
self.s = self.s[:-1] # 回溯,删除最后添加的字符
def letterCombinations(self, digits):
if len(digits) == 0:
return self.result
self.backtracking(digits, 0)
return self.result
文章来源:https://blog.csdn.net/niuzai_/article/details/135278562
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
最新文章
- Python教程
- 深入理解 MySQL 中的 HAVING 关键字和聚合函数
- Qt之QChar编码(1)
- MyBatis入门基础篇
- 用Python脚本实现FFmpeg批量转换
- flutter报错Cannot hit test a render box that has never been laid out
- python:logging 日志模块详解
- [论文精读] 使用扩散模型生成真实感视频 - 【李飞飞团队新作,文生视频 新基准】
- ssmPython在线学习平台(开题+源码)
- php学习-实战项目
- 编码下的雪景:如何用HTML和JS让雪花在屏幕上舞动
- C: AES对称加密算法代码
- UDP分片与丢包,UDP真的比TCP高效吗?
- 制造业数字化转型顶层设计业务架构和应用架构规划方法
- 有意思、好用的免费API分享