算法练习 Day24 | leetcode 77. 组合

一、回溯知识

1.题目分类

2.回溯模板

void backtracking(参数) {
    if (终止条件) {
        存放结果;
        return;
    }

    for (选择：本层集合中元素（树中节点孩子的数量就是集合的大小）) {
        处理节点;
        backtracking(路径，选择列表); // 递归
        回溯，撤销处理结果
    }
}

二、算法题

77. 组合

题目链接

1.未剪枝优化

class Solution {
    List<List<Integer>> result=new ArrayList<>();
    List<Integer> path=new LinkedList<>();
    public List<List<Integer>> combine(int n, int k) {
        backtracking(n, k, 1);
        return result;

    }

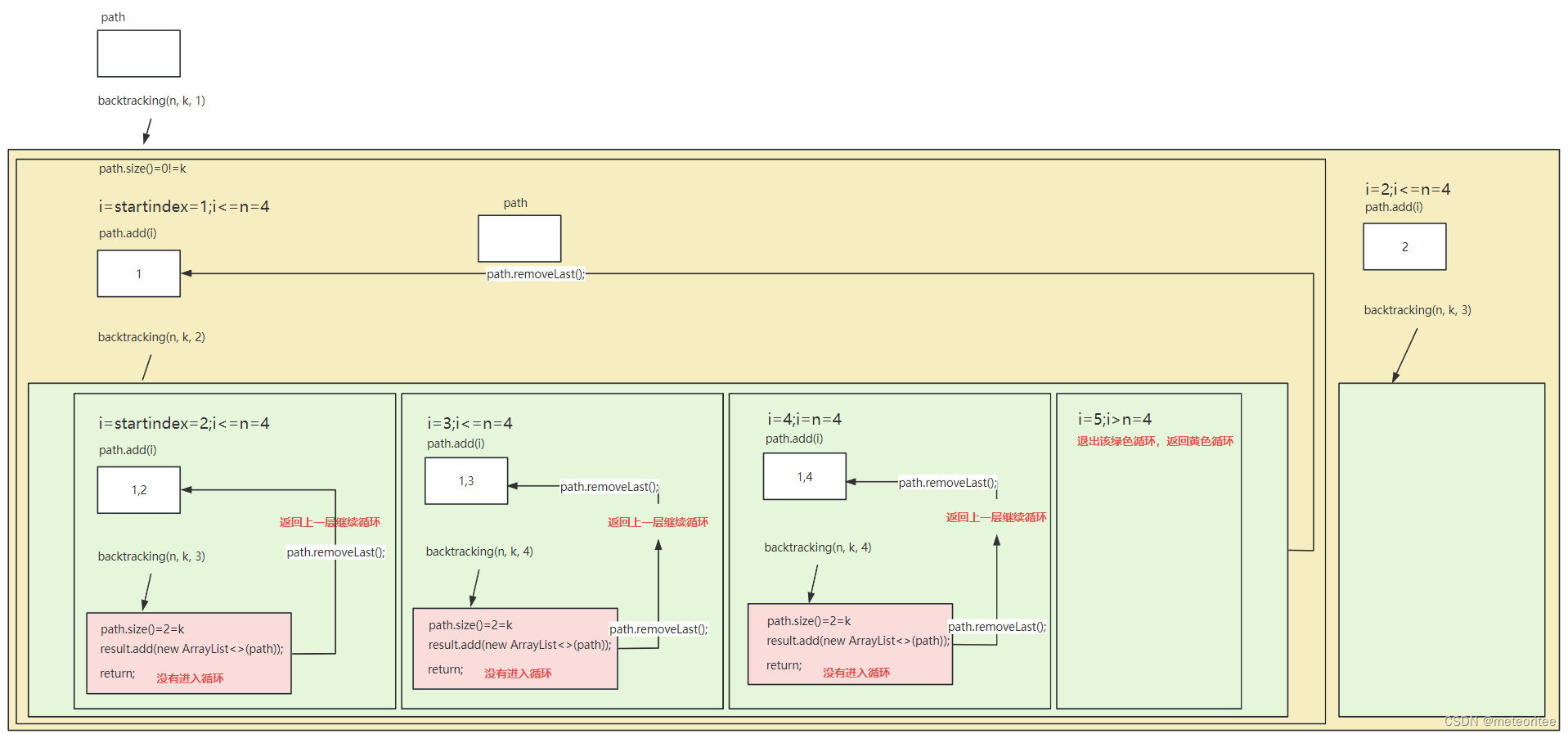
    public void backtracking(int n,int k,int startindex){
        //回溯函数终止条件
        if(path.size()==k){
            //当path的大小与组合大小相同时，说明找到了题目要求的组合，是回溯终止的情况
            result.add(new ArrayList<>(path));
            return;
        }
        for(int i=startindex;i<=n;i++){
            path.add(i);
            backtracking(n, k, i+1);
            path.removeLast();
        }

    }
}

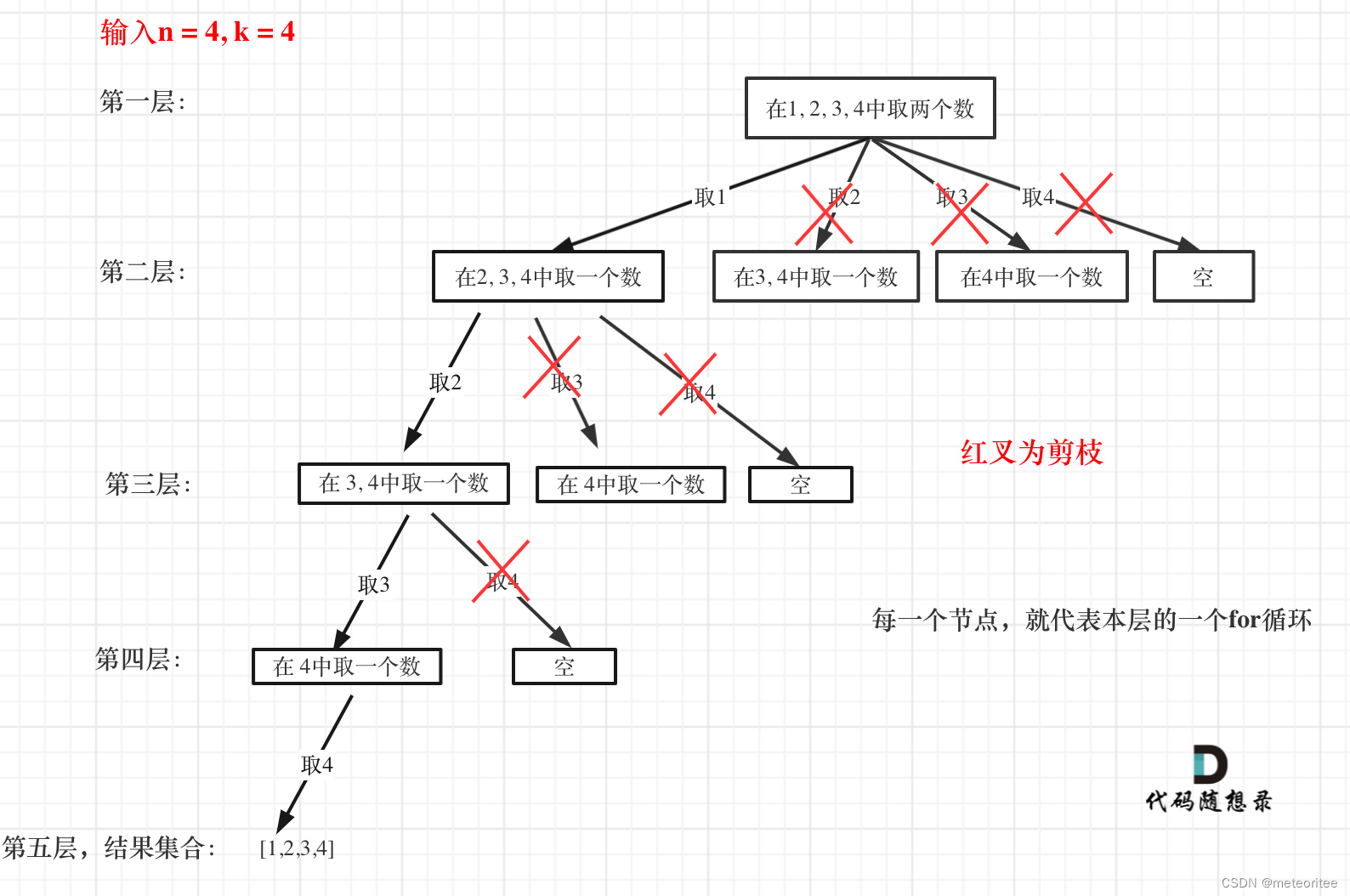
• startIndex?为了防止出现重复的组合

• result.add(new ArrayList<>(path))这种写法是为了防止在后续的过程中对 `path` 对象的修改影响到已经加入 `result` 中的组合。
  • 如果直接使用 `result.add(path)`，那么在后续的回溯过程中，当从 `path` 中移除元素时，已经加入 `result` 的组合也会受到影响，因为它们引用的是相同的 `path` 对象
  • 通过使用 `new ArrayList<>(path)`，实际上是创建了 `path` 的一个副本，使得 `result` 中的组合与后续的回溯过程互相独立，避免了相互影响。
  • 这样做是为了确保 `result` 中的组合是独立的，而不会因为后续回溯的修改而导致错误的结果。

2.剪枝优化

class Solution {
    List<List<Integer>> result=new ArrayList<>();
    List<Integer> path=new LinkedList<>();
    public List<List<Integer>> combine(int n, int k) {
        backtracking(n, k, 1);
        return result;

    }

    public void backtracking(int n,int k,int startindex){
        //回溯函数终止条件
        if(path.size()==k){
            //当path的大小与组合大小相同时，说明找到了题目要求的组合，是回溯终止的情况
            result.add(new ArrayList<>(path));
            return;
        }
        for(int i=startindex;i<=n-(k-path.size())+1;i++){
            path.add(i);
            backtracking(n, k, i+1);
            path.removeLast();
        }

    }
}

• ?只修改了循环中的i的判断条件

  • 已经选择的元素个数：path.size();

  • 还需要的元素个数为: k - path.size();

  • 下一个选取的元素在集合n的起始位置 : n - (k - path.size()) + 1，开始遍历

    • 比如

    • 取了1后，n - (k - path.size()) + 1=2，下一个元素要从2开始选，直接选定开始元素为1，不再尝试取2，3，4为开头，然后进入下一层循环

  • 为什么有个+1呢，因为包括起始位置，我们要是一个左闭的集合。

    举个例子，n