Prim算法：如何快速求解最小生成树？

一、普里姆（Prim）算法概述

Prim算法是图论中的一种算法，可在加权连通图里搜索最小生成树。

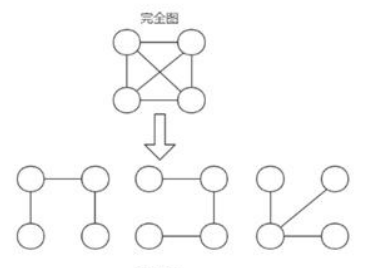
最小生成树，简称MST。是给定一个带权的无向联通图，如何选取一颗生成树，使树上所有边权的总和为最小，这个树就叫最小生成树。最小生成树有以下特点：

1. N个顶点，一定有N-1条边
2. 包含全部顶点
3. N-1条边都在图中

这个算法的常见用途就是在包含n个顶点的连通图中，找出只有（n - 1）条边包含所有n个顶点的连通子图，也就是最小生成树。

---

二、普里姆（Prim）算法的基本思路

Prim算法的思路如下：

1. 设G=(V，E)是连通网，T=(U，D)是最小生成树，V,U是顶点集合，E,D是边集合。
2. 若从顶点u开始构造最小生成树，则从集合V中取出顶点u放进集合U中，并标记顶点v的visted[u]=1，表示该顶点已经使用（已经连通）。
3. 若集合U中顶点ui与顶点V-U中的顶点vj之间存在边，则寻找这些边中的权值最小的边，但不构成回路，将顶点vj加入集合U中，将边（ui，vj）加入集合D中，标记visted[u]=1
4. 重复步骤2，直到U与V相等，即所有顶点都被标记为已经访问过，此时D中有N-1条边

估计看了这个思路，人都蒙了，没事，继续看看下面的图解就会一目了然了。

---

三、Prim算法实战

1584. 连接所有点的最小费用 - 力扣（LeetCode）

在力扣1584题，是求坐标轴上的点的最小生成树，具体题目请看上述链接。

解题思路：使用Prim算法。

1. 根据顶点的信息，生成邻接表
2. 定义几个变量
   • record：记录已经使用过的点
   • recordDistance： 用来存储每个未被选中的点到record的最短距离。若已经被放入record中则设置为-1
3. 初始化变量
   • 将第0个顶点作为生成最小生成树的起始顶点
   • 初始化recordDistance，记录其他未使用的订单到最小生成树的最小距离，由于一开始最小生成树只有一个节点，于是最小距离就是其余顶点到这个最小生成树的节点的距离，也就是weight[0][i]
4. 开始构造最小生成树
   • 遍历recordDistance，找出其余顶点到最小生成树的最小距离，记录其下标以及最小距离。
   • 收集得到的最小距离
   • 将该下标的recordDistance最小距离设置为-1，表示已经使用了
     1. 更新recordDistance数组，更新其余顶点到最小生成树的最小距离，Math.min(recordDistance[i], weight[minIndex][i])，因为最小生成树新增了一个节点，那么有可能导致其他顶点到这个新增的节点的距离更近，于是需要更新recordDistance。

class Solution {
    public int minCostConnectPoints(int[][] points) {
        // 最终结果
        int result = 0;
        // 邻接表
        int[][] weight = new int[points.length][points.length];
        // 初始化邻接表
        for (int i = 0; i < points.length; i++) {
            for (int j = i + 1; j < points.length; j++) {
                weight[i][j] = weight[j][i] = Math.abs(points[i][0] - points[j][0]) + Math.abs(points[i][1] - points[j][1]);
            }
        }
        // 记录已经使用过的点
        List<Integer> record = new ArrayList<>();
        // 记录其余点到上一个点的距离，如果为-1，说明该点已经使用了
        int[] recordDistance = new int[points.length];
        // 将第0个点设置为顶点
        record.add(0);
        recordDistance[0] = -1;
        // 更新距离
        for (int i = 1; i < points.length; i++) {
            recordDistance[i] = weight[0][i];
        }
        // 开始找点
        while (record.size() < points.length) {
            // 距离最短的顶点下标
            int minIndex = 0;
            // 最短距离
            int minDistance = Integer.MAX_VALUE;
            for (int i = 0; i < recordDistance.length; i++) {
                if (recordDistance[i] != -1 && recordDistance[i] < minDistance) {
                    minIndex = i;
                    minDistance = recordDistance[i];
                }
            }
            record.add(minIndex);
            result += minDistance;
            recordDistance[minIndex] = -1;
            // 更新顶点对应的最小距离
            for (int i = 0; i < points.length; i++) {
                if (recordDistance[i] != -1){
                    recordDistance[i] = Math.min(recordDistance[i], weight[minIndex][i]);
                }
            }

        }
        return result;
    }
}

---