python解决二叉搜索树范围和

对于给定一颗二叉搜索的根节点root及两个节点的值left和right，这里的left总是大于right的，返回大小在二者之间所有节点的值的和，这个二叉搜索树需要保证每个节点具有唯一值。

给定的二叉树如下：

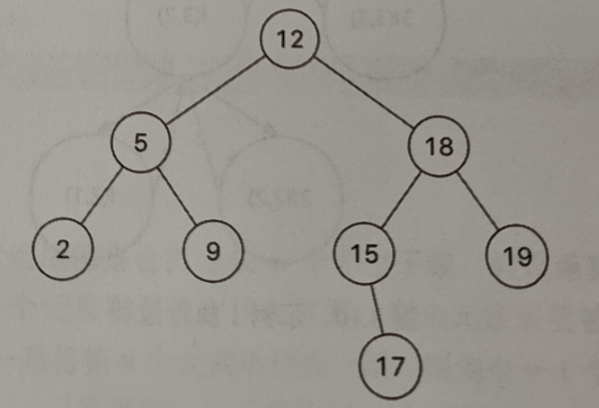
添加图片注释，不超过 140 字（可选）

对应的输出为：

添加图片注释，不超过 140 字（可选）

另一个二叉搜索树如下：

添加图片注释，不超过 140 字（可选）

对应输出为：

添加图片注释，不超过 140 字（可选）

对于该问题的解决思路，最直接的想法就是去遍历这颗二叉树的每个节点，将每个节点的值与left与right对比，将符合要求的节点累加，泽阳的时间复杂度与节点数相关，空间复杂度与树的高度相关，但是使用这一思路的话并没有合理的利用到二叉搜索树的特点，由于二叉搜索树及其所有子树具有左子树小于根节点，右子树大于根节点的特点，所以可以利用这一特点在遍历的过程中减少一些一部分多余的遍历，当根节点小于left时候，其左子树的所有节点均小于left，所以是不可能满足条件的，而当根节点大于right的时候，其右子树的所有节点均大于right的值，也是不可能满足条件的，这样对于这两类树的时候就不需要继续遍历了，减小了遍历的同时提高了效率。

以第二个例子为例，首先是当根节点8为参数的时候，执行深度优先搜索内嵌函数dfs，由于8是介于3和19之间的，对值进行累加并对其左右子树进行递归，由于节点17的左右子树均为空，所以累加之后进行出栈行为，然后就是节点15的左子节点入栈，累加计数后出栈

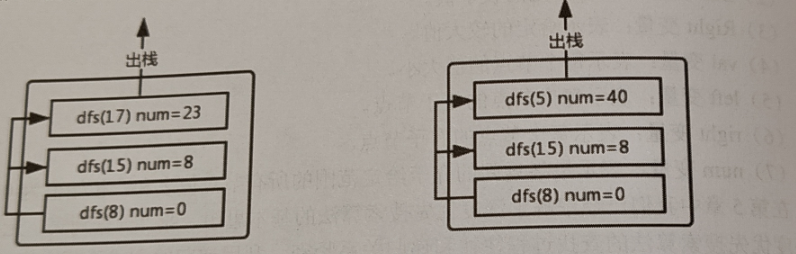
添加图片注释，不超过 140 字（可选）

python代码实现如下：

class Solution:   
    def findNode(self, root, Left, Right):
        def dfs(root):
            if root:
                if root.val<Left:
                    dfs(root.right)
                elif root.val>Right:
                    dfs(root.left)
                else:
                    self.num+=root.val
                    dfs(root.right)
                    dfs(root.left)
        self.num=0
        dfs(root)
        return self.num