浮点数表示法以及相关“小”知识点
浮点数的表示形式
小数点的位置是浮动的。
任意一个二进制数N可 以表示成:N=S×r^j
其中,S为尾数(可正可负),r为基数(数值),j是阶码(可正可负)。

1、对一个真值为+23.25的十进制数,用浮点数格式表示其原码。?
解:(23.25)10 =(10111.01)2
????????浮点数表示其原码为: 0.1011101×2^101
????????机器中表示为:
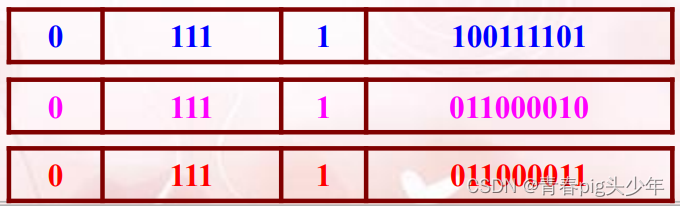
2、十进制数-79.25,用浮点数格式表示其原码、反码和补码。
解:(-79.25)10 =(-1001111.01)2
浮点数表示其原码为:1.100111101×2^+111
浮点数表示其反码为:1.011000010×2^+111
浮点数表示其补码为:1.011000011×2^+111
?规格化浮点数
若不对浮点数的表示做出明确规定,同一个浮点数的表示就具有不唯一性。
为了提高运算的精度,需要充分地利用尾数的有效 数位,通常采取浮点数规格化形式,即规定尾数的最高数位必须是一个有效值。
以基数为2说明规格化的格式
尾数M是原码表示,尾数的最高位为1是规格化形式, 即必须满足0.5≤|M|<1。
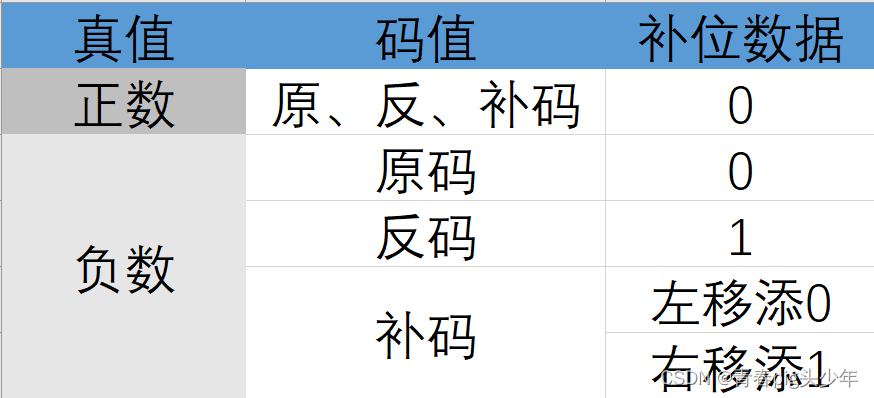
正数:尾数应为0.1x…x
负数:尾数应为1.1x…x
尾数M是补码表示,尾数的最高位与数符符号位相反为规格化形式。
正数:尾数应为0.1x…x,即0.5≤M<1
负数:尾数应为1.0x…x,即-1≤M<-0.5
当尾数不是规格化数时,就要通过修改阶码并同时左右移动尾数使其变为规格化数,这一过程称为规格化。
- 当基数为2时,尾数左移一位,阶码减1,称为 向左规格化(左归)。
- 当基数为2时,尾数右移一位,阶码加1,称为 向右规格化(右归)。
移位后补0还是1?
1、把非规格化的浮点数N=0.0110×2^11规格化。
解:浮点数N的尾数向左移一位(或尾数的小数点 右移一位),变成0.1100。
???????阶码递减1,得到N=0.1100×2^10
2、把浮点数-37.125进行规格化表示。
解:(-37.125)10=(-100101.001)2
????????规格化表示:1.100101001×2^110?
3、把二进制浮点数0.000110101进行规格化表示。
解:(0.000110101)2=(0.110101)2×2^-11
????????规格化表示:0.110101×2^-11
4、把二进制浮点数-10011111进行规格化表示。
解:(-10011111)2=(1.10011111)2×2^1000
????????规格化表示:1.10011111×2^1000?
IEEE754标准浮点数

- 数符表示浮点数的正负,与尾数是分开的。
- 阶码用移码来表示,一般情况下,阶码是在指数 上加一个常数,分别为7FH和3FFH。
- 尾数通常用原码的规格化表示,最高位总为1, 这一位通常不予存储。?
32位的IEEE754标准定义格式

注:1 8 23 +7F?
64位的IEEE754标准定义格式?

1 11 52 +3FF?
后续以32位单精度浮点数为例,其偏移值为127,尾数有一位隐藏位,一个规格化的32位浮点数X的值可表示为: X=(-1)^S×(1.M)×2^E-127?
1、十进制数178.125转换为二进制数,按照754的 标准进行规格化表示,总位数32位。
解:178.125=(10110010.001)2 =1.0110010001×2^111
????????数符:0
????????阶码:0000 0111+0111 1111=1000 0110
????????尾数:1. 011 0010 0010 0000 0000 0000(第一位隐藏不存储)
????????结果:? ?0; 10000110; 01100100010000000000000
2、十进制数100.25转换为二进制数,按照754的标 准进行规格化表示,总位数32位。
解:100.25=(1100100.01)2 =1.10010001×2^110
????????数符:0
????????阶码:0000 0110+0111 1111=1000 0101
????????尾数:1. 100 1000 1000 0000 0000 0000(第一位隐藏不存储)
????????结果:? ?0; 10000101; 10010001000000000000000
3、十进制数-1.5转换为二进制数,按照754的标准 进行规格化表示,总位数32位。(2018年西电考研)
解:-1.5= (-1.1)2 = -1.1×2^0
????????数符:1
????????阶码:0000 0000+0111 1111=0111 1111
????????尾数:1. 100 0000 0000 0000 0000 0000(第一位隐藏不存储)
????????结果:? ?1; 01111111; 100 0000 0000 0000 0000 0000
4、利用754表示的32位浮点数C1C90000H转换成为十进制数。
解:由题意可得,步骤如下:
- 十六进制展开二进制,分离出符号位、阶码和尾数
C1C90000H= 1; 100 0001 1; 100 1001 0000 0000 0000 000- 计算出阶码真值(移码-偏置值) 10000011-01111111=100
- 以规格化二进制数形式写出此数 -1.1001001×2^100
- 写成非规格化二进制数形式 -11001.001
- 转换成十进制数,并加上符号位 (-11001.001)2=(-25.125)10
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
- Python教程
- 深入理解 MySQL 中的 HAVING 关键字和聚合函数
- Qt之QChar编码(1)
- MyBatis入门基础篇
- 用Python脚本实现FFmpeg批量转换
- synchronized语法与Before/After模式
- GO设计模式——23、空对象模式(行为型)
- AcWing:4646. 爬树的甲壳虫
- 如何用AI帮你写年会贺词
- 医药公司行业特性及解决方案-CRM
- 【Vue】什么是nextTick?
- 科技助力教育:数字化如何改变家校社协同育人?
- CANopen DS402 Homing方法分析
- 计算机毕业设计 基于SpringBoot的餐厅点餐管理系统的设计与实现 Java实战项目 附源码+文档+视频讲解
- Java 注解解析获取及自定义