【深蓝学院】手写VIO第11章--Square Root Bundle Adjustment

1. 文章贡献

这篇文章最大的贡献在于证明了对$Jl$进行QR分解，对normal equation左乘$Q^T$等价于Schur compliment，即证明了(14)(16)是等价的。如此则无需makeHessian，可以使用float代替double，加快BA求解速度。

左乘$Q^T$能够使得问题转化为Schur补相同的问题，因为如果$\Delta x_p^{?}$固定，则一定能找到$\Delta x_l^{?}$使得第一项为0，所以可直接优化第二项得出$\Delta x_P^{?}$(与Schur compliment marg掉landmark效果相同)，即式(17)，本文使用CG迭代求解$\Delta x_p^{?}$。

2. 在Jacobian中添加$\sqrt{damp}$等价于在Hessian中添加damp

这里的理解参照Ceres源码中的注释，在Jacobian和Hessian中添加阻尼因子方法有所区别，但效果相同，下面会给予证明。

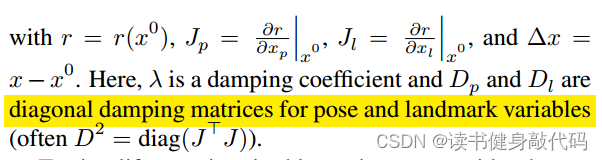
参照这种方法来理解式(6)，其实加入的阻尼因子是在Jacobian的行最后加的，$||Ax?b|{|}^2和$||Dx||^2$优化的并不是同一个x，但是，如下所示：

简单证明，设Jacobian为
$$\left[\begin{array}{c}a,b,c\end{array}\right]$$
设$a，b$分别为camera pose，$c$为landmark，为了简化，我们将$a，b，c$均看做标量。

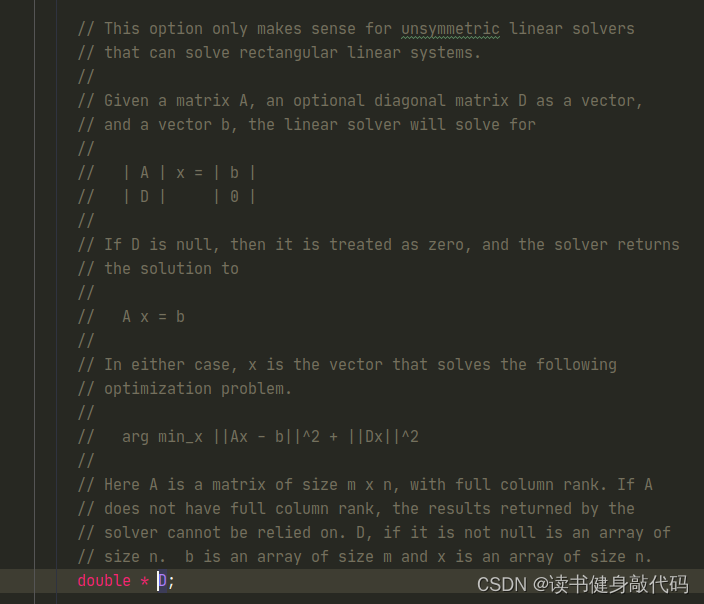
从上图可以看出，在Jacobian矩阵和Hessian矩阵中添加阻尼因子的方法是不同的，但是效果是等价的。之前在VINS-MONO拓展1中我们直接对Hessian进行操作，直接将与Hessian相同维度的对角阵 $\lambda I$ 叠加到Hessian上去，但是对于Jacobian，是按照上图所示的方法按行叠加在Jacobian最下测，这也解释了Ceres中为什么构建D矩阵时为什么要开根号，因为Ceres内部是直接对Jacobian进行叠加，而非Hessian：

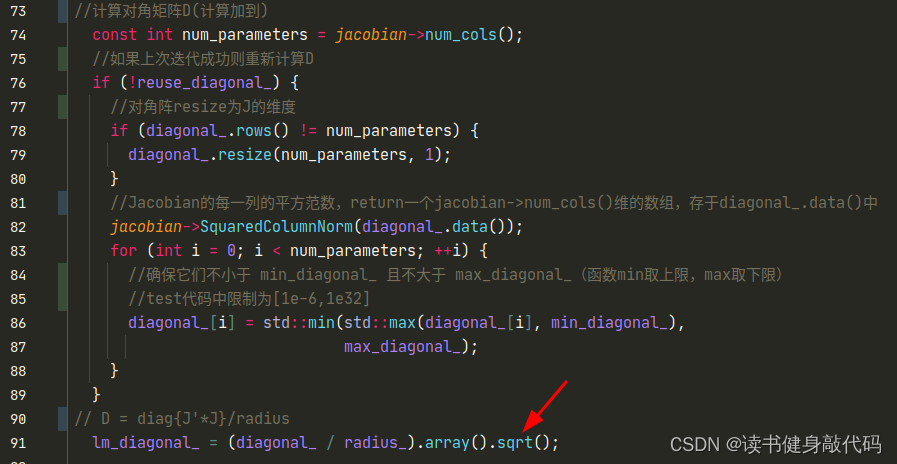
$\lambda$是以开根号的形式加入的，且和Jacobian有关，这样能在VIO这种情形避免加入的lambda过大（IMU数据过大，1e6级别）。

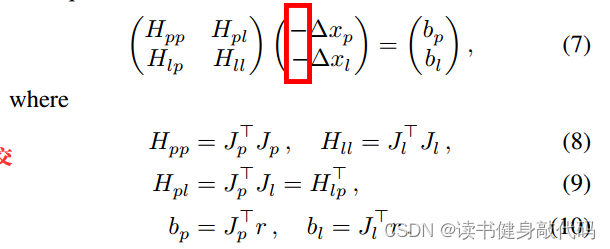
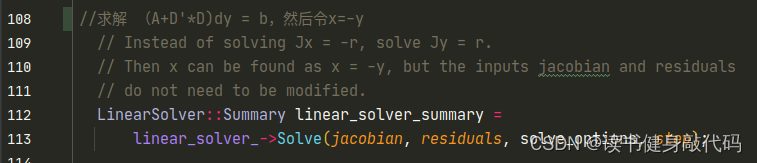
从式(7)可以看出论文作者应该是参考了Ceres的源码的，ceres中y即为$?\Delta x$。

2. Givens旋转

矩阵的QR分解方法有：householder，Givens rotation等。
之前在对初始$J_l$进行QR分解时使用了householder方法，但是速度较慢，Givens旋转较快，原理是通过初等行变换(又叫做Givens rotation吉文斯旋转)，我们之前学习线性代数肯定接触到过这类操作。QR分解的Givens旋转目的是将$J_l$化为上三角矩阵$R$，而构建的$Q_{\lambda }$即为$J_L$分解后的$Q$，当$Q_{\lambda }$构建完成之后，QR分解也就完成了。
关于Givens矩阵的原理以及如何构建，可以参考这篇知乎

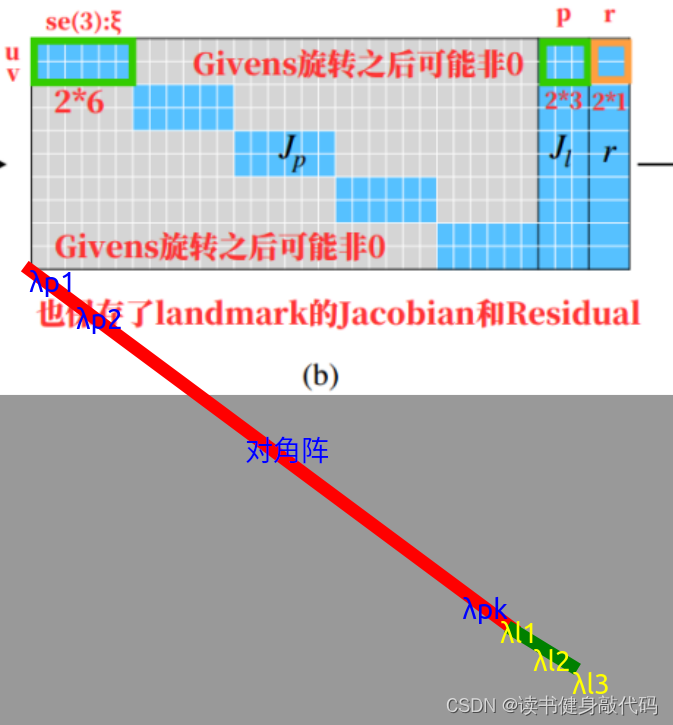
根据论文中的Dense landmark blocks，我构建了如下所示的A矩阵（这里没有考虑外参$Tbc$和fix camera pose[0],[1]的情况，2*6即为camera pose的Jacobian block，43，44，45block是添加的landmark damp），构建了$Q_{\lambda }$，完成了A矩阵的rollback

实验代码：

#include <iostream>
#include <Eigen/Core>
#include "../include/utility.hpp"

using Scalar = float;

#define Q_LAMBDA //是否构建Q_labmda来执行回退

void small_test() {
    Eigen::Matrix<Scalar, 3, 2> A;
    A << 1.0, 2.0, 3.0, 4.0, 5.0, 6.0;

    std::cout << "Original Matrix A:\n" << A << "\n\n";
    // 构造 Givens 旋转矩阵
    Eigen::JacobiRotation<Scalar> gr;

    gr.makeGivens(A(0,0), A(2,0));
    A.applyOnTheLeft(0, 2, gr.adjoint());
    std::cout << "Matrix A after G1:\n" << A << "\n";
    A(2, 0) = 0;

    gr.makeGivens(A(0,0), A(1,0));
    A.applyOnTheLeft(0, 1, gr.adjoint());
    std::cout << "Matrix A after G2:\n" << A << "\n";
    A(1, 0) = 0;

    gr.makeGivens(A(1,1), A(2,1));
    A.applyOnTheLeft(1, 2, gr.adjoint());
    std::cout << "Matrix A after G3:\n" << A << "\n";
    A(2, 1) = 0;
    std::cout << "Matrix A after Givens rotation:\n" << A << "\n";
}

void big_test() {
    Eigen::Matrix<Scalar, 9, 16> A;
    A << 1.0, 2.0, 3.0, 4.0, 5.0, 6.0, 0, 0, 0, 0, 0, 0, 37, 38, 39, 46,
            7, 8, 9, 10, 11, 12, 0, 0, 0, 0, 0, 0, 0, 40, 41, 47,
            13, 14, 15, 16, 17, 18, 0, 0, 0, 0, 0, 0, 0, 0, 42, 48,
            0, 0, 0, 0, 0, 0, 19, 20, 21, 22, 23, 24, 0, 0, 0, 0,
            0, 0, 0, 0, 0, 0, 25, 26, 27, 28, 29, 30,0,0,0,0,
            0, 0, 0, 0, 0, 0, 31, 32, 33, 34, 35, 36,0,0,0,0,
            0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 43,0,0,0,
            0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,0,44,0,0,
            0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,0,0,45,0;

    std::cout << "Original Matrix A:\n" << A << "\n\n";
    // 构造 Givens 旋转矩阵
    Eigen::JacobiRotation<Scalar> gr;
#ifndef Q_LAMBDA
    Scalar G1_arr;
    gr.makeGivens(A(0,12), A(6,12), &G1_arr);
    Eigen::JacobiRotation<Scalar> G1 = gr.adjoint();
    A.applyOnTheLeft(0,6, G1);
    std::cout << "Matrix A after G1:\n" << A << "\n";
    A(6, 12) = 0;

    std::cout << "G1_arr: " << G1_arr << std::endl;
    std::cout << "Original Rotation cos: " << gr.c() << "\t" << " sin:\t" << gr.s() << "\n\n";
    std::cout << "Givens Adjoint cos: " << gr.adjoint().c() << "\t" << " sin:\t" << gr.adjoint().s() << "\n\n";
    std::cout << "Givens transpose cos: " << gr.transpose().c() << "\t" << " sin:\t" << gr.transpose().s() << "\n\n";
    std::cout << "Givens Rotation:\n" << gr.adjoint().c() << "\t" << -gr.adjoint().s() << "\n\n"
              << gr.adjoint().s() << "\t" << gr.adjoint().c() << "\n\n";
    //针对实数，adjoint()和transpose()是等价的，makeGivens()根据传入参数cos和sin，我们可以外部构建出Givens，相当于把向量逆时针旋转：
    // cos  -sin
    // cos   sin
    //applyOnTheLeft()中不知道为什么只能用.adjoint()，.adjoint()实际上构建了一个新的对象，其中cos取共轭，sin取反，JacobiRotation(conj(m_c), -m_s)
    //只不过在applyOnTheLeft()中可能有根据A的行数构建一个主对角线为1，其他为0的真正可左乘到A上的Givens矩阵
    //至于joan sola的公式(5.16)，可能和Eigen中的实现有些出入，其cos的符号对不上公式，后面再说

    gr.makeGivens(A(1,13), A(7,13));
    Eigen::JacobiRotation<Scalar> G2 = gr.adjoint();
    A.applyOnTheLeft(1,7, G2);
    std::cout << "Matrix A after G2:\n" << A << "\n\n";
//    A(7, 13) = 0;

    gr.makeGivens(A(1,13), A(6,13));
    Eigen::JacobiRotation<Scalar> G3 = gr.adjoint();
    A.applyOnTheLeft(1,6, G3);
    std::cout << "Matrix A after G3:\n" << A << "\n\n";
//    A(6, 13) = 0;

    gr.makeGivens(A(2,14), A(8,14));
    Eigen::JacobiRotation<Scalar> G4 = gr.adjoint();
    A.applyOnTheLeft(2,8, G4);
    std::cout << "Matrix A after G4:\n" << A << "\n\n";
//    A(8, 14) = 0;

    gr.makeGivens(A(2,14), A(7,14));
    Eigen::JacobiRotation<Scalar> G5 = gr.adjoint();
    A.applyOnTheLeft(2,7, G5);
    std::cout << "Matrix A after G5:\n" << A << "\n\n";
//    A(7, 14) = 0;

    gr.makeGivens(A(2,14), A(6,14));
    Eigen::JacobiRotation<Scalar> G6 = gr.adjoint();
    A.applyOnTheLeft(2,6, G6);
    std::cout << "Matrix A after G6:\n" << A << "\n\n";
//    A(6, 14) = 0;
#else
    Eigen::Matrix<Scalar, 9, 16> B = A; //B用于跟使用Q_lambda作对比
    Eigen::Matrix<Scalar, 9, 16> C = A;
    Eigen::Matrix<Scalar, 9, 9> Q_lambda = Eigen::Matrix<Scalar, 9, 9>::Identity();//整体Q_lambda
    Eigen::Matrix<Scalar, 9, 9> Q_lambda_C = Eigen::Matrix<Scalar, 9, 9>::Identity();//整体Q_lambda
    //G1
    gr.makeGivens(A(0,12), A(6,12));
    Eigen::Matrix<Scalar, 9, 9> tmpQ = Eigen::Matrix<Scalar, 9, 9>::Identity();
    tmpQ(0,0) = gr.c();
    tmpQ(0,6) = -gr.s();
    tmpQ(6,0) = gr.s();
    tmpQ(6,6) = gr.c();
    Q_lambda = tmpQ * Q_lambda;
    A = tmpQ * A;
    C.applyOnTheLeft(0,6, gr.adjoint());
    Q_lambda_C.applyOnTheLeft(0,6, gr.adjoint());
    std::cout << "G1 tmpQ: \n" << tmpQ << "\n\n";
    std::cout << "after G1 Q_lambda: \n" << Q_lambda << "\n\n";
    std::cout << "Matrix A after G1:\n" << A << "\n\n";

    //G2
    gr.makeGivens(A(1,13), A(7,13));
    tmpQ.setIdentity();
    tmpQ(1,1) = gr.c();
    tmpQ(1,7) = -gr.s();
    tmpQ(7,1) = gr.s();
    tmpQ(7,7) = gr.c();
    Q_lambda = tmpQ * Q_lambda;
    A = tmpQ * A;
    C.applyOnTheLeft(1,7, gr.adjoint());
    Q_lambda_C.applyOnTheLeft(1,7, gr.adjoint());
    std::cout << "G2 tmpQ: \n" << tmpQ << "\n\n";
    std::cout << "after G2 Q_lambda: \n" << Q_lambda << "\n\n";
    std::cout << "Matrix A after G2:\n" << A << "\n\n";

    //G3
    gr.makeGivens(A(1,13), A(6,13));
    tmpQ.setIdentity();
    tmpQ(1,1) = gr.c();
    tmpQ(1,6) = -gr.s();
    tmpQ(6,1) = gr.s();
    tmpQ(6,6) = gr.c();
    Q_lambda = tmpQ * Q_lambda;
    A = tmpQ * A;
    C.applyOnTheLeft(1,6, gr.adjoint());
    Q_lambda_C.applyOnTheLeft(1,6, gr.adjoint());
    std::cout << "G3 tmpQ: \n" << tmpQ << "\n\n";
    std::cout << "after G3 Q_lambda: \n" << Q_lambda << "\n\n";
    std::cout << "Matrix A after G3:\n" << A << "\n\n";

    //G4
    gr.makeGivens(A(2,14), A(8,14));
    tmpQ.setIdentity();
    tmpQ(2,2) = gr.c();
    tmpQ(2,8) = -gr.s();
    tmpQ(8,2) = gr.s();
    tmpQ(8,8) = gr.c();
    Q_lambda = tmpQ * Q_lambda;
    A = tmpQ * A;
    C.applyOnTheLeft(2,8, gr.adjoint());
    Q_lambda_C.applyOnTheLeft(2,8, gr.adjoint());
    std::cout << "G4 tmpQ: \n" << tmpQ << "\n\n";
    std::cout << "after G4 Q_lambda: \n" << Q_lambda << "\n\n";
    std::cout << "Matrix A after G4:\n" << A << "\n\n";

    //G5
    gr.makeGivens(A(2,14), A(7,14));
    tmpQ.setIdentity();
    tmpQ(2,2) = gr.c();
    tmpQ(2,7) = -gr.s();
    tmpQ(7,2) = gr.s();
    tmpQ(7,7) = gr.c();
    Q_lambda = tmpQ * Q_lambda;
    A = tmpQ * A;
    C.applyOnTheLeft(2,7, gr.adjoint());
    Q_lambda_C.applyOnTheLeft(2,7, gr.adjoint());
    std::cout << "G5 tmpQ: \n" << tmpQ << "\n\n";
    std::cout << "after G5 Q_lambda: \n" << Q_lambda << "\n\n";
    std::cout << "Matrix A after G5:\n" << A << "\n\n";

    //G6
    gr.makeGivens(A(2,14), A(6,14));
    tmpQ.setIdentity();
    tmpQ(2,2) = gr.c();
    tmpQ(2,6) = -gr.s();
    tmpQ(6,2) = gr.s();
    tmpQ(6,6) = gr.c();
    Q_lambda = tmpQ * Q_lambda;
    A = tmpQ * A;
    C.applyOnTheLeft(2,6, gr.adjoint());
    Q_lambda_C.applyOnTheLeft(2,6, gr.adjoint());
    std::cout << "G6 tmpQ: \n" << tmpQ << "\n\n";
    std::cout << "after G6 Q_lambda: \n" << Q_lambda << "\n\n";
    std::cout << "Matrix A after G6:\n" << A << "\n\n";

    //执行旋转
    std::cout << "Matrix A==B before Givens rotation:\n" << B << "\n\n";
    B = Q_lambda * B;
    std::cout << "Matrix A after Givens rotation:\n" << A << "\n\n";
    std::cout << "Matrix B after Givens rotation:\n" << B << "\n\n";
    std::cout << "Matrix C after Givens rotation:\n" << C << "\n\n";
#endif


#ifndef Q_LAMBDA
    //使用6个Givens矩阵rollback G1.T * G2.T * G3.T * G4.T * G5.T * G6.T * A
    A.applyOnTheLeft(2,6, G6.transpose());
    A.applyOnTheLeft(2,7, G5.transpose());
    A.applyOnTheLeft(2,8, G4.transpose());
    A.applyOnTheLeft(1,6, G3.transpose());
    A.applyOnTheLeft(1,7, G2.transpose());
    A.applyOnTheLeft(0,6, G1.transpose());
    std::cout << "Matrix A after Givens.T rotation rollback:\n" << A << "\n\n";
#else
    //使用Q_lambda.T 执行rollback
    A = Q_lambda.transpose() * A;
    std::cout << "Matrix A after Givens.T rotation rollback:\n" << A << "\n\n";

    B = Q_lambda.transpose() * B;
    std::cout << "Matrix B after Givens.T rotation rollback:\n" << B << "\n\n";

    C = Q_lambda_C.transpose() * C;
    std::cout << "Matrix C after Givens.T rotation rollback:\n" << C << "\n\n";

#endif
}

int main(int argc, char** argv) {
//    small_test();   //小规模测试
    big_test();     //大规模测试
}

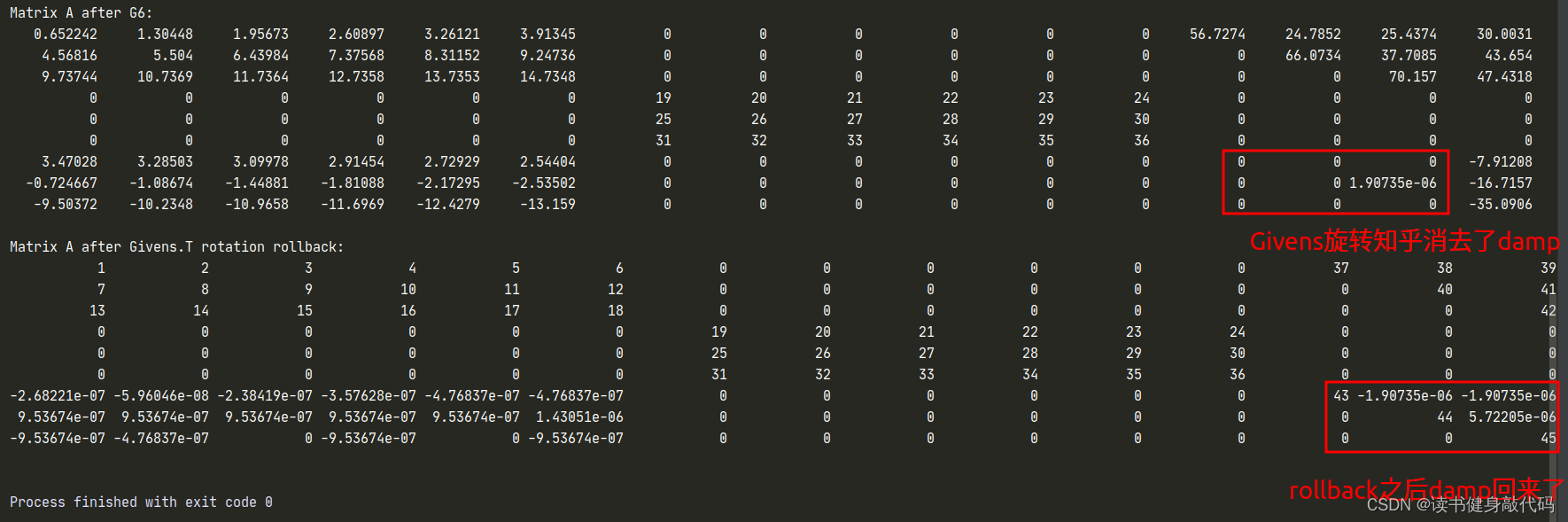
消去damp共需6个Givens矩阵，消去顺序遵照如下顺序，参考博客

从左到右逐列执行。
每一列，从下往上执行。
每一次的Givens矩阵由要消为0 的元素和对应对角线的元素确定。

对应此处，构建Givens旋转需要的元素分别为G1(37,43)， G2(40, 44)，G3(40,44上面一个)，G4(42, 45)，G5(42, 45上面一个)，G6(42, 45上面第2个)，注意，在构建过程中，由于A矩阵需要不断乘G，元素会发生变化，所以上面的元素分别指的是original A矩阵中这个元素位置所代表的元素。

构建Givens矩阵需要构建Eigen::JacobiRotation<Scalar>对象，调用Eigen函数makeGivens()，算出sin和cos，Givens矩阵形式即为
$$\left[\begin{array}{cc}cos\theta & ?sin\theta \\ sin\theta & cos\theta \end{array}\right]$$

Givens矩阵的应用，可以调用makeGivens()函数，也可以手动构建Givens矩阵，然后左乘$J_l$。

故有3种测试和实现思路：

1. step by step构建G1~G6，并保存，并不显式构建$Q_{\lambda }$和$G$(这也是论文中所说的方法)，
   
   在构建过程中分别调用applyOnTheLeft左乘到A矩阵上去(注意需要.adjoint())，即
   $$\begin{array}{r}{A}^{\prime }=G_6{G}_5{G}_4{G}_3{G}_2{G}_{1}A\end{array}\text{\hspace{1em}?}$$
   则
   $$\begin{array}{r}{Q}_{\lambda }=G_6{G}_5{G}_4{G}_3{G}_2{G}_1\end{array}\text{\hspace{1em}?}$$
   rollback阶段调用6次applyOnTheLeft()函数执行rollback：
   $$\begin{array}{r}{Q}_{\lambda }^T=(G_6{G}_5{G}_4{G}_3{G}_2{G}_1{)}^T=G_1^T{G}_2^T{G}_3^T{G}_4^T{G}_5^T{G}_6^T\end{array}\text{\hspace{1em}?}$$
   $$\begin{array}{r}A=G_1^T{G}_2^T{G}_3^T{G}_4^T{G}_5^T{G}_6^T{A}^{\prime }\end{array}\text{\hspace{1em}?}$$
   在代码中把#define Q_LAMBDA宏注释掉即可，结果如下：
   

2. 开启#define Q_LAMBDA宏，显式构建$Q_{\lambda }$和$G$，在构建过程中直接使用矩阵乘法而非applyOnTheLeft函数作用于$A$，$Q_{\lambda }$构建完成后，执行B = Q_lambda * B;来测试A，B是否相等，最后同样使用$Q_{\lambda }^T$来rollback，2和3的测试结果一起给出。

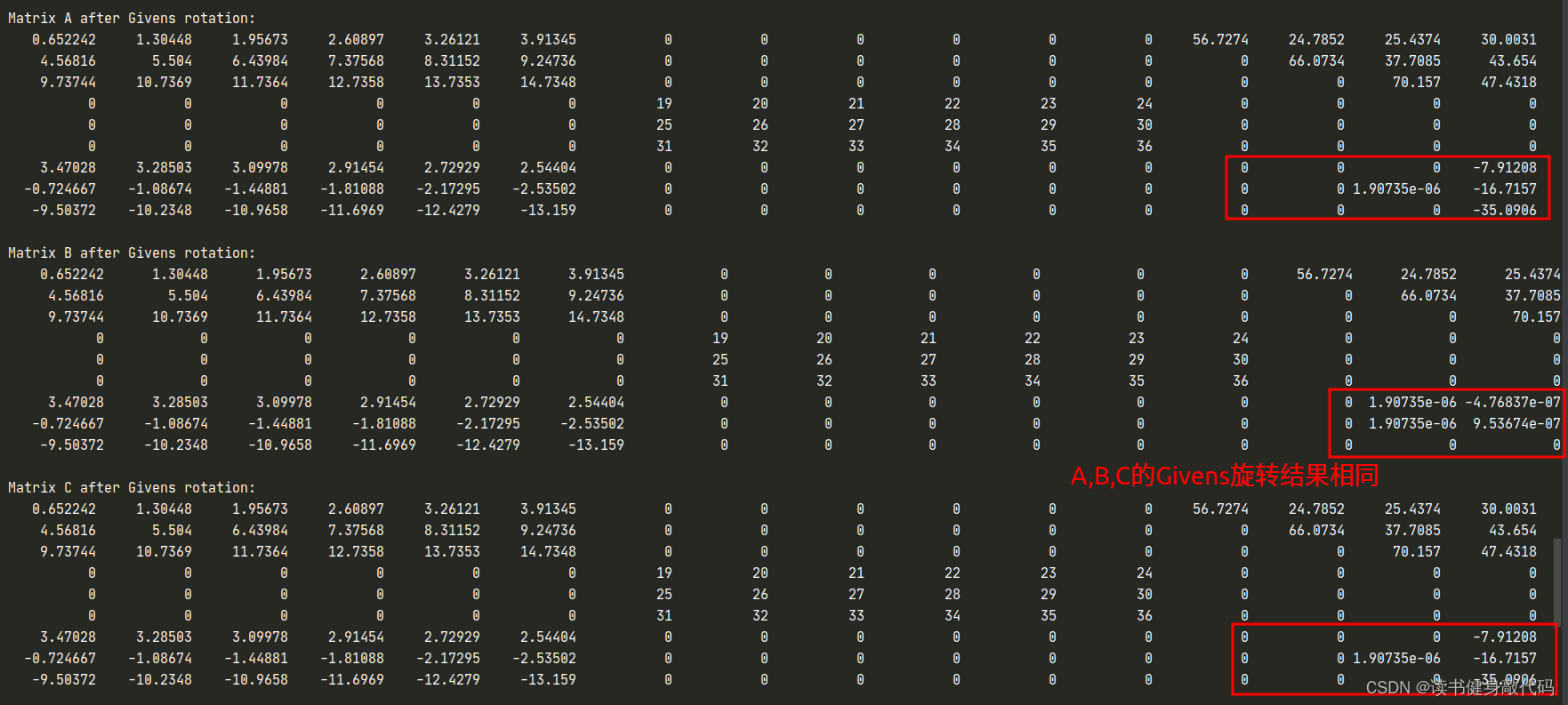
3. 开启#define Q_LAMBDA宏，不显式构建$G$，但是使用applyOnTheLeft函数显式构建$Q_{\lambda }$(注意需.adjoint())，对应代码中的Q_lambda_C，使用$Q_{\lambda }^T$完成rollback，结果如下：
   
   

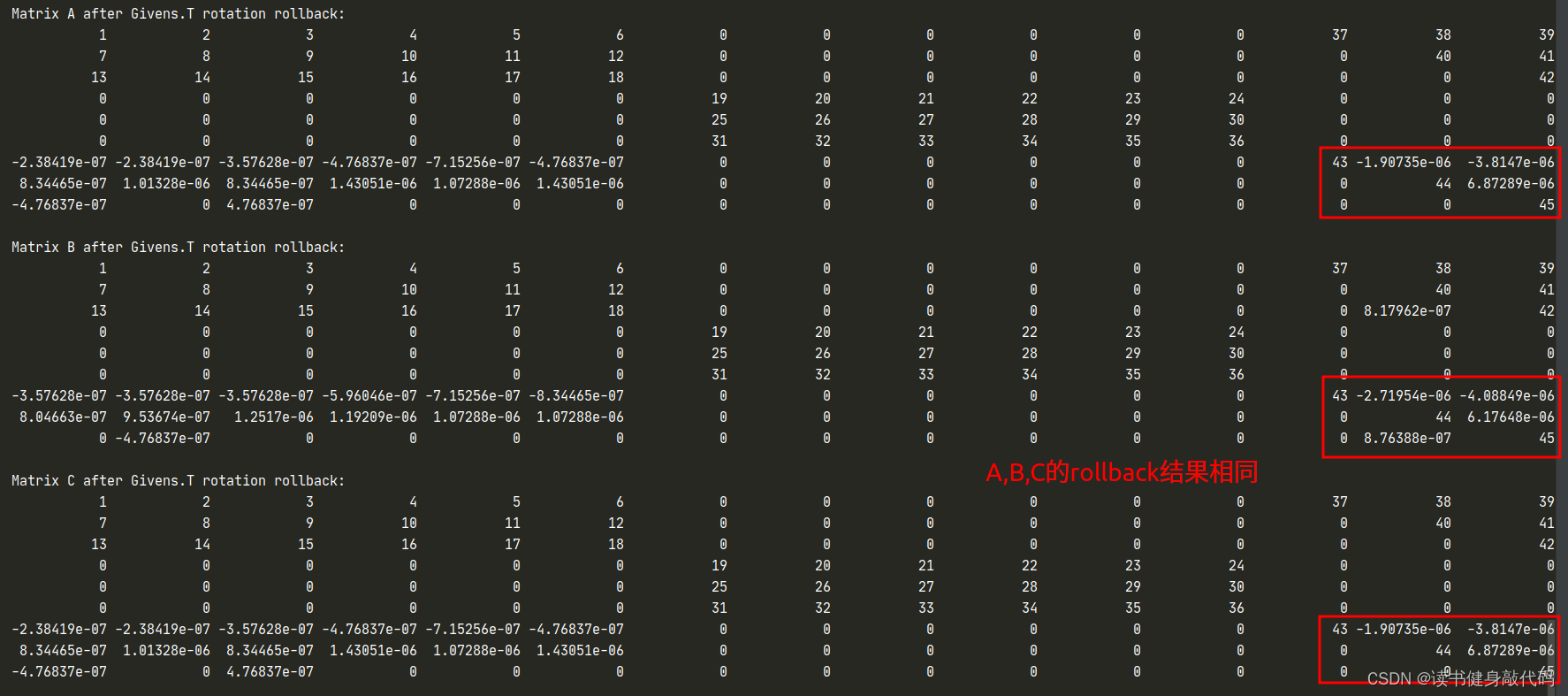
至此，完成了Givens旋转add damp以及rollback的代码实现，可以继续添加到LM中，在复现过程中我使用了上述方法3。

---

joan sola这篇文献中计算cos，sin的方法如下，但是在Eigen中不是这样计算的，留心注意一下，

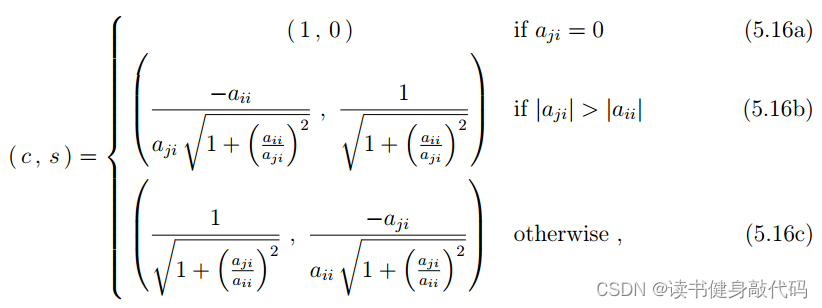
Eigen中该部分代码如下：

// specialization for complexes
template<typename Scalar>
void JacobiRotation<Scalar>::makeGivens(const Scalar& p, const Scalar& q, Scalar* r, internal::true_type)
{
  using std::sqrt;
  using std::abs;
  using numext::conj;
  
  if(q==Scalar(0))
  {
    m_c = numext::real(p)<0 ? Scalar(-1) : Scalar(1);
    m_s = 0;
    if(r) *r = m_c * p;
  }
  else if(p==Scalar(0))
  {
    m_c = 0;
    m_s = -q/abs(q);
    if(r) *r = abs(q);
  }
  else
  {
    RealScalar p1 = numext::norm1(p);
    RealScalar q1 = numext::norm1(q);
    if(p1>=q1)
    {
      Scalar ps = p / p1;
      RealScalar p2 = numext::abs2(ps);
      Scalar qs = q / p1;
      RealScalar q2 = numext::abs2(qs);

      RealScalar u = sqrt(RealScalar(1) + q2/p2);
      if(numext::real(p)<RealScalar(0))
        u = -u;

      m_c = Scalar(1)/u;
      m_s = -qs*conj(ps)*(m_c/p2);
      if(r) *r = p * u;
    }
    else
    {
      Scalar ps = p / q1;
      RealScalar p2 = numext::abs2(ps);
      Scalar qs = q / q1;
      RealScalar q2 = numext::abs2(qs);

      RealScalar u = q1 * sqrt(p2 + q2);
      if(numext::real(p)<RealScalar(0))
        u = -u;

      p1 = abs(p);
      ps = p/p1;
      m_c = p1/u;
      m_s = -conj(ps) * (q/u);
      if(r) *r = ps * u;
    }
  }
}

3. Jacobian推导

复现过程中添加了imu，虽然外参$T_{bc}$设置为$Identity()$，但Jacobian和纯视觉不同，需要重新推导。

类似于VINS-MONO中的推导，参考博客，这里直接给出$p_w$，更简单。

视觉pose部分：

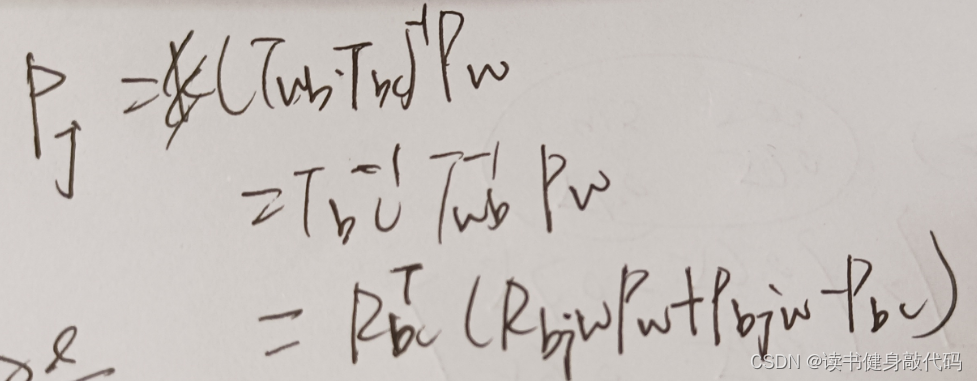
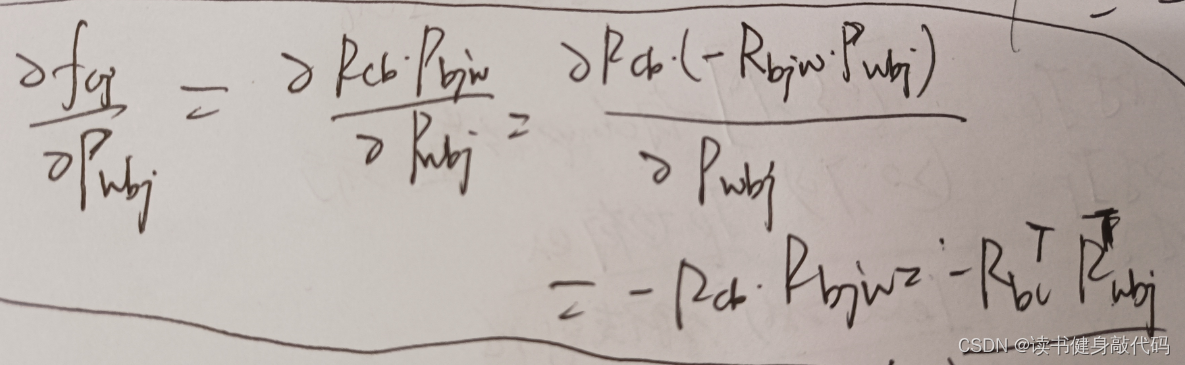
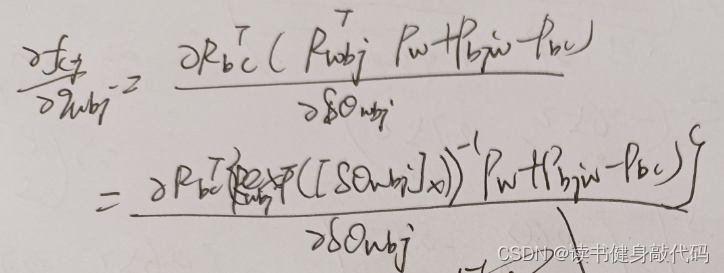
外参部分：

4. Refernece

[1] Demmel, N., Sommer, C., Cremers, D., & Usenko, V.C. (2021). Square Root Bundle Adjustment for Large-Scale Reconstruction. 2021 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), 11718-11727.

[2] Sol, J. (2017). Course on SLAM.