【数据结构】一些数组面试题以及顺序表的思考

简单不先于复杂，而是在复杂之后。

1. 数组相关面试题

1.原地移除数组中所有的元素val，要求时间复杂度为O(N)，空间复杂度为O(1)。

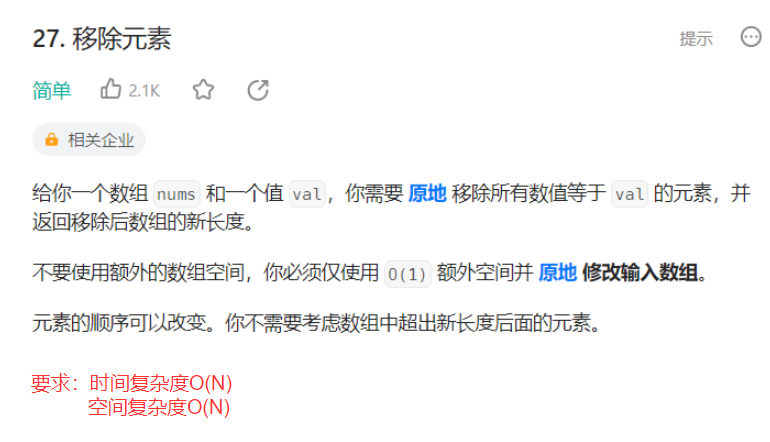
int removeElement(int* nums, int numsSize, int val) {
    int src = 0, dst = 0;
    while(src < numsSize)
    {
        if(nums[src] != val)
        {
            nums[dst] = nums[src];
            ++src;
            ++dst;
        }
        else
        {
            ++src;
        }
    }

    return dst;
}

2.删除排序数组中的重复项。

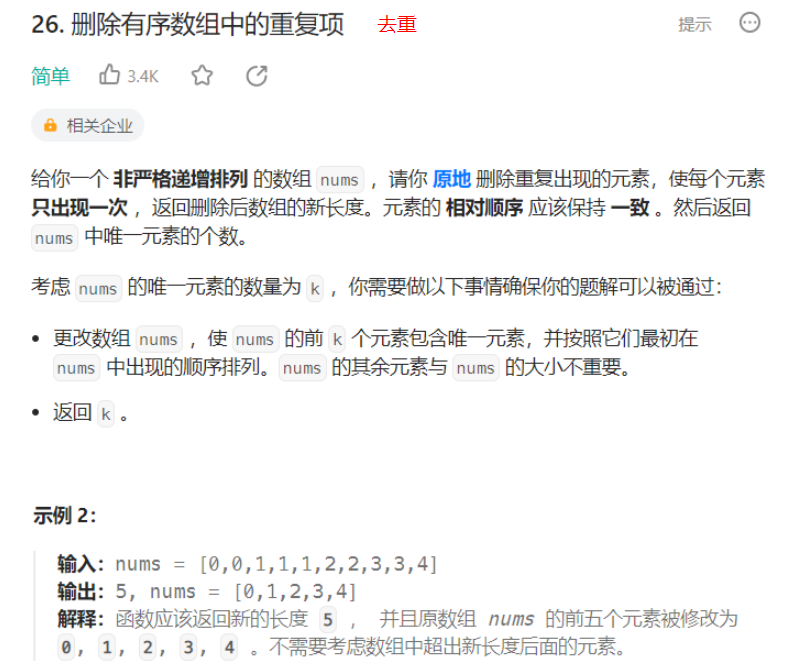
int removeDuplicates(int* nums, int numsSize) {
    int src = 0, dst = 0;
    while(src < numsSize)
    {
        if(nums[src] == nums[dst])
        {
            ++src;
        }
        else
        {
            nums[++dst] = nums[src++];
        }
    }

    return dst + 1;
}

3.合并两个有序数组。

若 nums1 的数先结束比较，那么可以不做任何操作，但是如果 nums2 先结束，就需要把 nums2 中剩余的数拷贝到 nums1 中

void merge(int* nums1, int nums1Size, int m, int* nums2, int nums2Size, int n) {
    int end1 = m - 1, end2 = n - 1;
    int i = m + n - 1;
    while(end1 >= 0 && end2 >= 0)
    {
        if(nums1[end1] > nums2[end2])
        {
            nums1[i] = nums1[end1];
            --i;
            --end1;
        }
        else
        {
             nums1[i] = nums2[end2];
             --i;
             --end2;
        }
    }

//end2 结束， nums2的数组都拷贝过去了，不用处理

//end1 结束， nums1的数组都拷贝过去了，需要再把nums2剩下的数据拷贝过去
    
    while(end2 >= 0)
    {
        nums1[i] = nums2[end2];
        --i;
        --end2;
    }
}

2. 顺序表的问题及思考

问题：

1. 中间/头部的插入删除，时间复杂度为O(N)
2. 增容需要申请新空间，拷贝数据，释放旧空间，会有不小的消耗。
3. 增容一般是呈2倍的增长，势必会有一定的空间浪费。例如当前容量为100，满了以后增容到200，我们再继续插入了5个数据，后面没有数据插入了，那么就浪费了95个数据空间。

思考：该如何解决以上问题?

–end1;
}
else
{
nums1[i] = nums2[end2];
–i;
–end2;
}
}

//end2 结束， nums2的数组都拷贝过去了，不用处理

//end1 结束， nums1的数组都拷贝过去了，需要再把nums2剩下的数据拷贝过去

while(end2 >= 0)
{
    nums1[i] = nums2[end2];
    --i;
    --end2;
}

}

### 2.4 顺序表的问题及思考

> 问题：
>
> 1. 中间/头部的插入删除，时间复杂度为O(N)
> 2. 增容需要申请新空间，拷贝数据，释放旧空间，会有不小的消耗。
> 3. 增容一般是呈2倍的增长，势必会有一定的空间浪费。例如当前容量为100，满了以后增容到200，我们再继续插入了5个数据，后面没有数据插入了，那么就浪费了95个数据空间。
>
> 思考：该如何解决以上问题?
>
> ?           **下篇文章我们来使用链表的结构。**