减小PAPR——PTS技术

---

前言

在正交频分复用（OFDM）系统中，峰均比（PAPR）是一个重要的性能指标。高 PAPR 会导致功率放大器（PA）的非线性失真，限制了系统的性能。为了抑制 PAPR，多种技术被提出，其中基于部分传输序列（PTS）的方法是一种有效目广泛使用的技术。本文利用 MATLAB 仿真，分析不同参数 V 对 PTS-PAPR 抑制技术的效果影响。

---

一、PTS-PAPR 抑制技术

1、简介

PTS-PAPR 抑制技术是一种基于部分传输序列的方法，通过将原始 OFDM 符号分解为多个部分序列，并在发射端以及接收端之间进行信号的组合，从而减小 PAPR。在 PTS 技术中，原始 OFDM 符号被分为 V 个部分序列，每个序列的长度为 N，并且这些序列之间存在相位旋转的关系。同时，通过选择合适的相位旋转因子，可以在接收端恢复原始 OFDM 符号。

2、原理

部分传输序列（PTS）技术将 $N$ 个符号的输入数据块分割为 $V$ 个不相交的子块：
$$X=[X^1,x^2,...,x^V{]}^T公式1$$
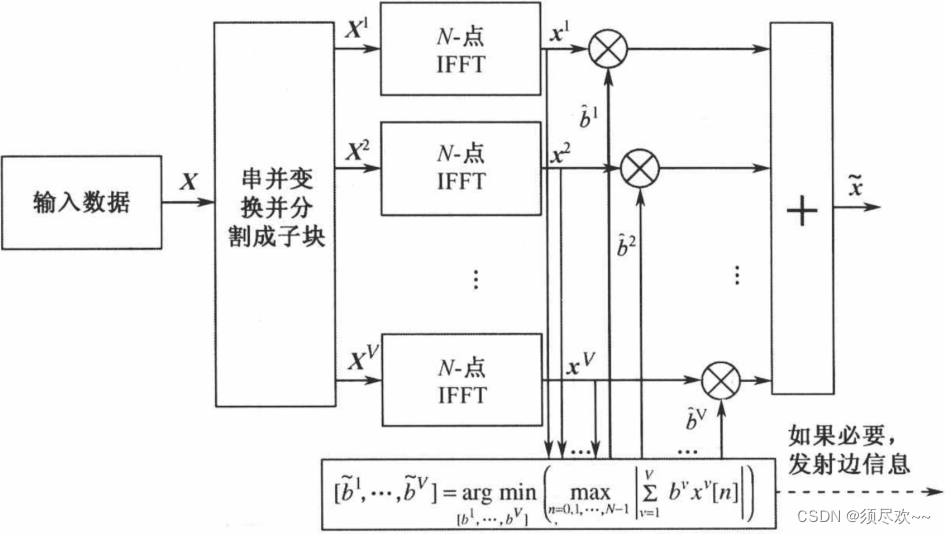
其中，$X^i$ 为连续分布、大小相同的子块。如图 1 所示，在 SLM 技术中对所有的子载波加扰，而在 PTS 技术中对每一个子块加扰（独立旋转相位）。每一个分割后的子块乘以一个相应的复相位因子 $b^v=e^{j?v}，v=1,\mathrm{2...},V$，随后经过 IFFT，得到：
x = I F F T ∑ v = 1 V b v X v = ∑ v = 1 V b v ? I F F T { X v } = ∑ v = 1 V b v x v 公式 2 x=IFFT{\sum_{v=1}^{V}b^vX^v}=\sum_{v=1}^{V}b^v\cdot IFFT\{X^v\}=\sum_{v=1}^{V}b^vx^v\quad \quad 公式2 x=IFFTv=1∑V?bvXv=v=1∑V?bv?IFFT{Xv}=v=1∑V?bvxv公式2
其中， { x v } \{x^v\} {xv} 为 PTS。选择相位向量，使得 PAPR 最小：

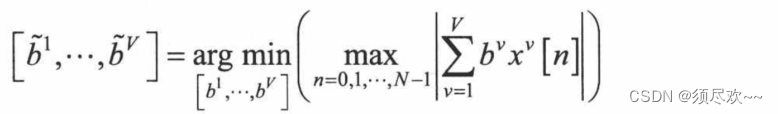
这样，最小 PAPR 向量的时域信号可以表示为：
$$\tilde{x}=\sum _{v=1}^V\widetilde{b^v}\widetilde{x^v}公式4$$

图1 用于减小 PAPR 的 PTS 技术的框图

为降低复杂度，尽在一个有限的集合中选择相位因子 { b v } v = 1 V \{b^v\}_{v=1}^{V} {bv}v=1V?。因为允许的相位因子集合是 b = { e j 2 π i / W ∣ i = 0 , 1 , . . . , W ? 1 } b=\{e^{j2\pi i/W}|i=0,1,...,W-1\} b={ej2πi/W∣i=0,1,...,W?1}，所以应该在 $W^{V?1}$ 个相位因子集合中搜索最佳的相位因子集合。因此，搜索的复杂度随子块数的增加呈指数上升。

对于每一个数据块，PTA 技术需要 $V$ 次 $IFFT$ 运算和 $[lo{g}_2^{W^V}]$ 比特的边信息。PTS 技术的 PAPR 性能不仅受子块数 $V$ 和允许的相位因子 $W$ 的影响，而且受子块分割的影响。实际中有三种子块分割方案:相邻、交叉和伪随机方案。在这些方案中，伪随机方案性能最好。

3、实现方法

正如前面讨论的，PTS 技术存在搜索最优相位向量集合时复杂度较高的问题，特别是当子块数增加时。下面文献提出了各种降低复杂度的方案。一个特别的例子是使用二进制相位因子 1,-1 的次优组合算法。

• 文献 1：Peak-to-Average Power Ratio Reduction of an OFDM SignalUsing Partial Transmit Sequences
• 文献 2：A coding technique for reducing peak-to-average power ratio in OFDM

现将其方法总结如下:

• ① 如公式 1 所示，将输入数据块分为 $V$ 个子块。
• ② 设置所有的相位因子 $b^v=1，v=1,2,...,V$，找到公式 2 中的 PAPR，将其设为 PAPR_min。
• ③ 设置 $v=2$
• ④ 在 $b^v=?1$ 的情况下，找到公式 2 的 PAPR
• ⑤ 如果 PAPR>PAPRmin，那么 $b^v=1$；否则，更新 PAPR=PAPR_min。
• ⑥ 如果 $v<V$，那么 $v$ 加 1，然后回到步骤 ④；否则，得到最优的相位因子 $\tilde{b}$，然后退出程序。

在次优的组合算法中对公式 2 计算 $V$ 次，远小于原来的 PTS 技术所需的计算次数，即 $V<<W^V$。

二、MATLAB 仿真

1、核心代码

 % --  相位因子最优化  -- %
   for m = 1:Nsb
      x = w(1:Nsb) * ifft_sym;                      % 公式2
      sym_pow = abs(x).^2;                          % 计算时域信号的功率（幅度的平方） 
      PAPR = max(sym_pow)/mean(sym_pow);            % 计算峰均比（PAPR）
      if m == 1
          PAPR_min = PAPR;                          % 找到公式2中的 PAPR，将其设为 PAPR_min
      else
          if PAPR_min < PAPR                        % 如果 PAPR>PAPR_min
              w(m)=1;                               % b=1
          else                                      % 否则
               PAPR_min = PAPR;                     % 更新 PAPR=PAPR_min 
          end
      end
      w(m+1)=-1;                                    % 在 w=-1 的情况下，找到公式2中的 PAPR
   end

2、仿真结果

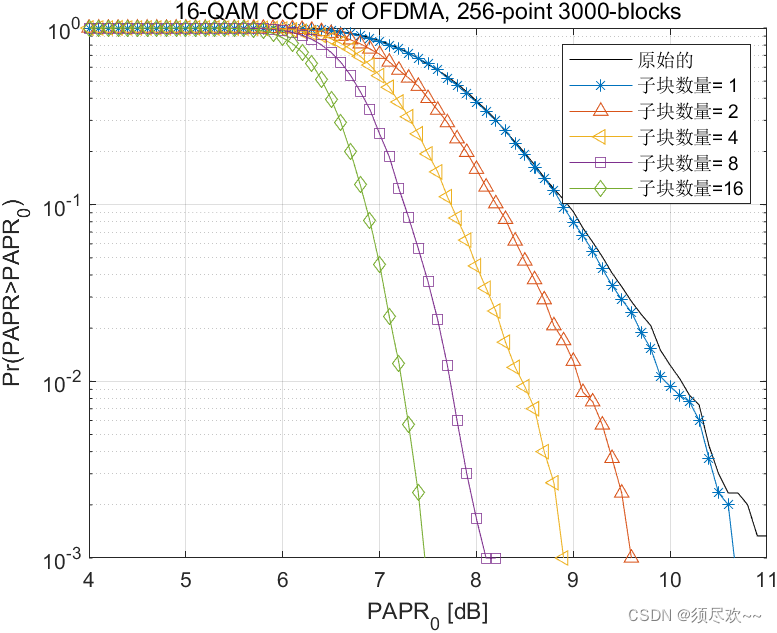
从仿真图中可以看出当子块数目增加时（$V=1,2,4,8,16$），PAPR 的性能提高了。

三、资源自取

源码注释清晰，有需要可自取~

链接：减小PAPR——PTS技术

---

我的qq：2442391036，欢迎交流！

---