机器人运动学——阿克曼小车

发布时间：2024年01月13日

机器人运动学是从几何角度描述和研究机器人的位置、速度和加速度随时间的变化规律的科学，它不涉及机器人本体的物理性质和加在其上的力。这里分享一下在学习阿克曼小车过程中，对运动学的正逆解的理解。

正解：已知机器人各个关节的运动，求解机器人本体x，y，z轴的运动。

逆解：已知机器人本体x，y，z轴方向的运动，求解各个关节的运动。

一、阿克曼转向几何

阿克曼转向几何是一种为了解决交通工具转弯时，内外转向轮路径指向的圆心不同的几何学。通常情况下，内侧轮胎转角更大。同时要求4个轮子运动方向垂直相交与一点，四个轮子按照同一个圆心旋转。如下图所示，为阿克曼机器人转向时的状态。

二、阿克曼小车

阿克曼机构结构简单、可靠性高，不需要过多的复杂部件，维护和保养成本较低，可以提高设备的使用寿命。

阿克曼小车运动原理分为很多情况，主要是直行状态下和转弯状态下。在直行状态下，小车各轮轮毂转速相同，因此直行状态下阿克曼小车前后两个轴都不需要转向。在转弯状态下，阿克曼小车前后轴的转向角度需要调整，使得车辆能够顺利完成转弯。以下以四轮的阿克曼小车为例，通过运动学分析，求解小车的转角和速度。

因为这台阿克曼小车是后驱的，所以求逆解时计算前轮的转角和后轮的速度，求正解的时候计算小车本体的速度。

?图1

?符号说明：

δ_l左前轮转角
δ_r右前轮转角
V_L左后轮速度
V_R右后轮速度
R转弯半径
W轮距
L轴距
V_x小车本体x方向速度
V_z小车本体z方向速度
W轮距
\omega

角速度

三、逆解

我们在已知小车本体目标速度V_x、V_y、V_z的情况下，求解前轮的转角δ_l、δ_r，以及后轮的线速度V_L、V_R。

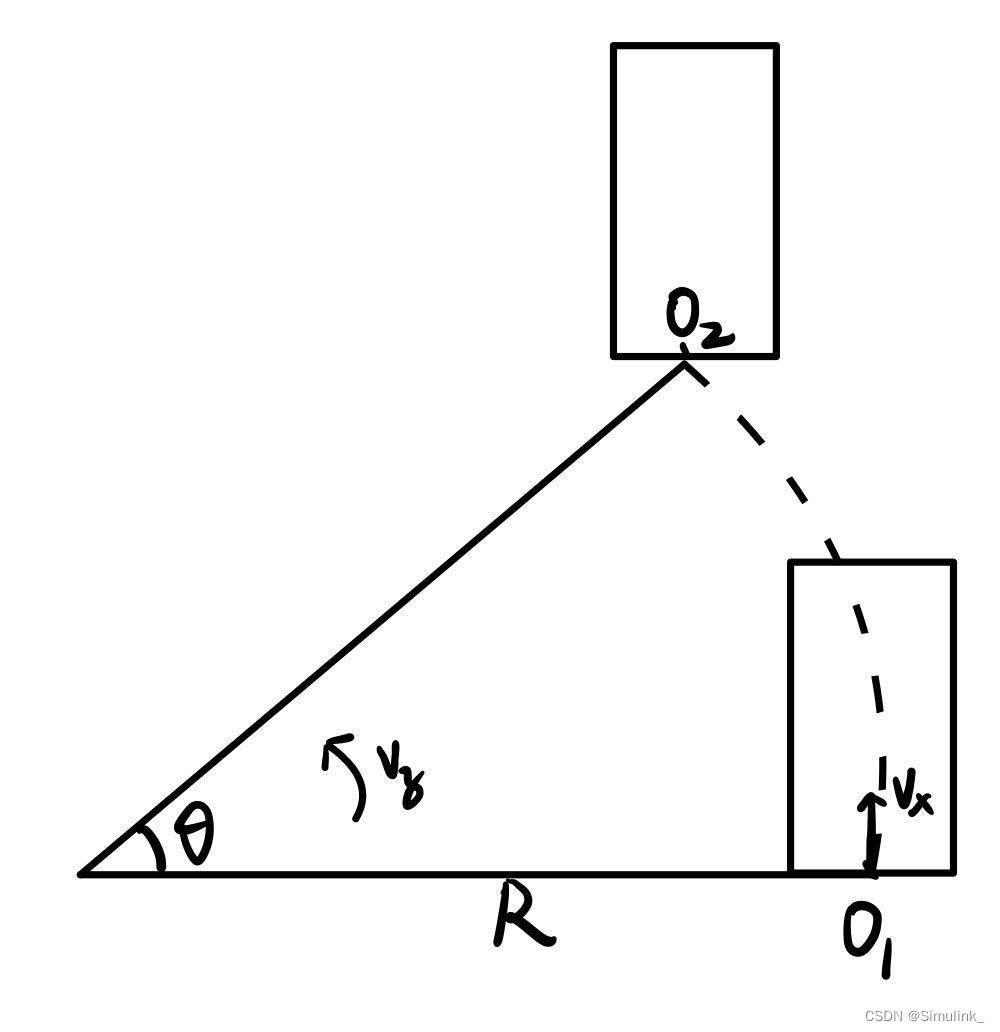
?图2

如图可以得到：O_1O_2=\theta R=V_xt

所以：?R=\frac{O_1O_2}{\theta }=\frac{V_xt}{\theta}=\frac{V_xt}{V_zt}=\frac{V_x}{V_z}，即求得了转弯半径R。

因为线速度和角速度之间存在着关系：V=\omega R

所以：V_L=\omega R_L = \omega (R-\frac{1}{2}W) = \frac{V_x}{R} (R-\frac{1}{2}W)

? ? ? ? ???V_R=\omega R_R = \omega (R+\frac{1}{2}W) = \frac{V_x}{R} (R+\frac{1}{2}W)

再有，通过图1中的几何关系，可以计算得到：

????????????????????????????????????????????????????????????????????????????\left\{\begin{matrix} \delta _l =tan^{-1}(\frac{L}{R-\frac{1}{2}W})\\ \delta _r =tan^{-1}(\frac{L}{R+\frac{1}{2}W}) \end{matrix}\right.

其实，图1中的前轮中点处的角度，还存在阿克曼角关系：\delta = \frac{\delta_l+\delta_r}{2}

四、正解

对于正解，相对来说就简单许多，

\quad \ V_L+V_R =\frac{V_x}{R} (R-\frac{1}{2}W) + \frac{V_x}{R} (R+\frac{1}{2}W)=2V_x \\ \\ \Rightarrow V_x = \frac{V_R +V_L}{2}

?????V_R-V_L =\frac{V_x}{R} (R+\frac{1}{2}W) - \frac{V_x}{R} (R-\frac{1}{2}W) =\frac{V_xW}{R}

因为R=\frac{V_x}{V_z}

所以：V_z = \frac{V_x}{R} =\frac{V_R-V_L}{V_xW}V_x = \frac{V_R-V_L}{W}

文章来源:https://blog.csdn.net/Simulink_/article/details/135536595
本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。
最新文章