Matlab 求解非刚性微分方程（ode45）

语法

1、[t,y] = ode45(odefun,tspan,y0)
2、[t,y] = ode45(odefun,tspan,y0,options)
3、[t,y,te,ye,ie] = ode45(odefun,tspan,y0,options)
4、sol = ode45(___)

描述

[t,y] = ode45(odefun,tspan,y0)
其中，tspan = [t0 tf] 为微分方程 odefun 的积分区间，y0 为初始条件
[t,y] = ode45(odefun,tspan,y0,options)
其中，options 可以定义积分设置，例如绝对误差容限
[t,y,te,ye,ie] = ode45(odefun,tspan,y0,options)
sol = ode45(___)
返回一个结构体，可以将该结构体与 deval 结合使用来计算区间 [t0 tf] 中任意点位置的解

示例

1、具有一个解分量的 ODE

$$y^{\prime }=2t,时间区间为[05]，初始条件为y_0=0$$

tspan = [0 5];  % 积分区间
y0 = 0;  % 初始条件
[t,y] = ode45(@(t,y) 2*t, tspan, y0);  % 求解计算
plot(t,y,'-o')  % 绘图

2、非刚性方程

二阶 ODE
$$y_1^{\prime \prime }?\mu (1?y_1^2)y_1^{\prime }+y_1=0$$

改写成一阶 ODE
$$\begin{array}{rl}{y}_1^{\prime }& =y_2\\ y_2^{\prime }& =\mu (1?y_1^2)y_2?y_1\end{array}$$

函数文件 vdp1.m 为 $\mu =1$ 的微分方程，变量 $y_1$ 和 $y_2$ 是二元素向量 dydt 的项 y(1) 和 y(2)。

function dydt = vdp1(t,y)
dydt = [y(2); (1-y(1)^2)*y(2)-y(1)];

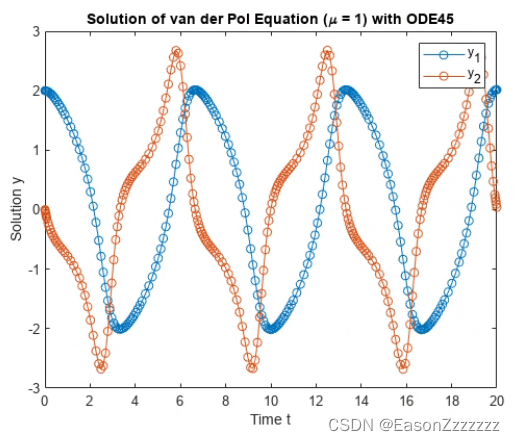
使用 ode45 函数、时间区间 [0 20] 和初始值 [2 0] 来解算该 ODE。生成的输出即为时间点 t 的列向量和解数组 y。

[t,y] = ode45(@vdp1,[0 20],[2; 0]);
plot(t,y(:,1),'-o',t,y(:,2),'-o')
title('Solution of van der Pol Equation (\mu = 1) with ODE45');
xlabel('Time t');
ylabel('Solution y');
legend('y_1','y_2')