八大排序——快速排序（霍尔 | 挖空 | 前后指针 | 非递归）

我们今天来讲讲八大排序中的快速排序，快速排序最明显的特点就是排序快，时间复杂度是O（N* logN），但是坏处就是如果排序的是一个逆序的数组的时候，时间复杂度是O（N^2）,还不用我们的插入排序好，所以特点明显，但是缺点也是很明显的，那我们开始今天的学习吧。

首先就是我们霍尔大佬的排序方法，思想就是一遍排序让大的在右边，小的都在左边，我们来看看下面的动图.

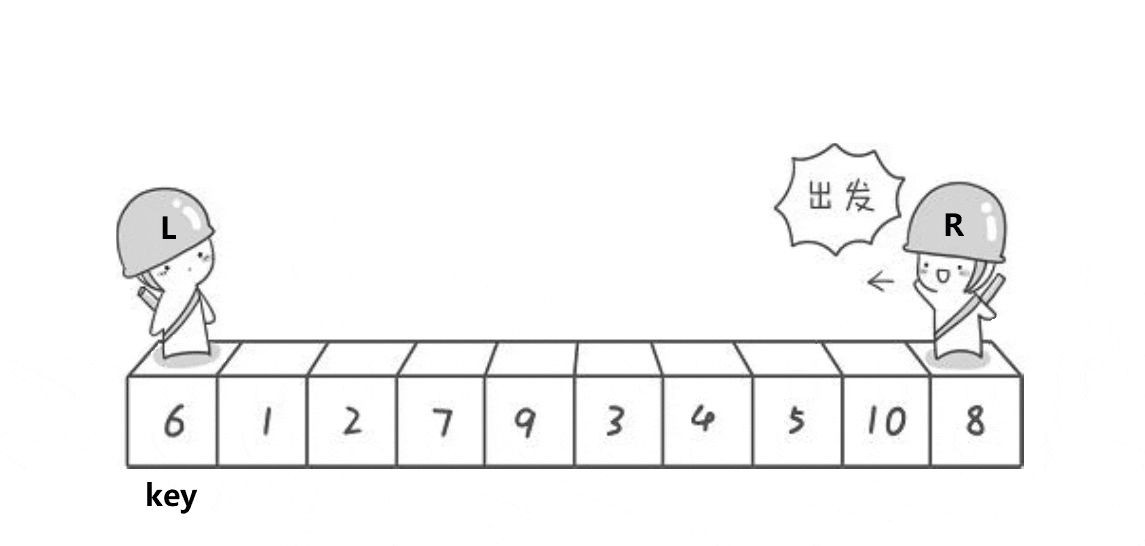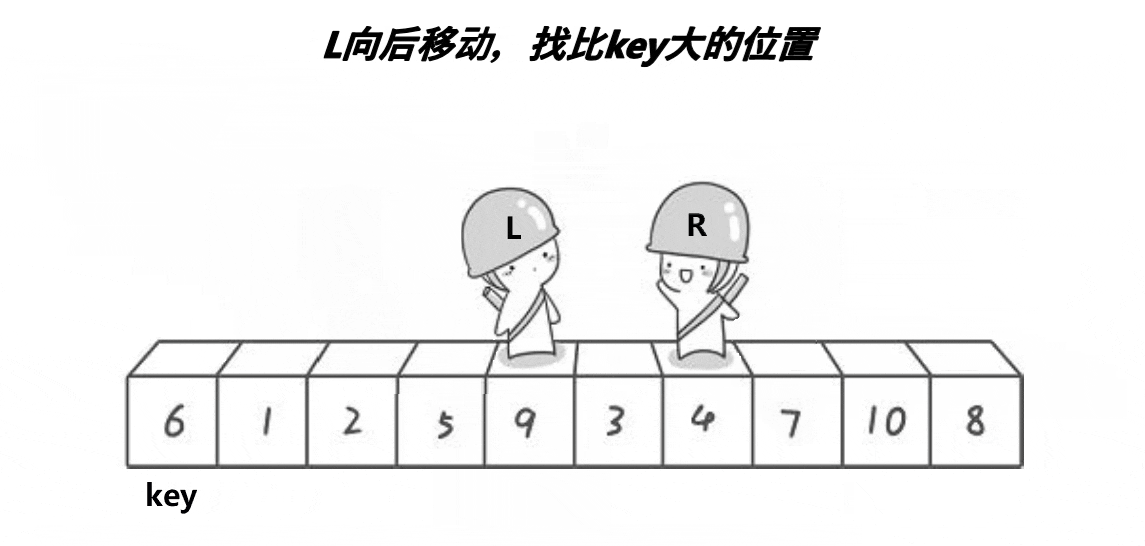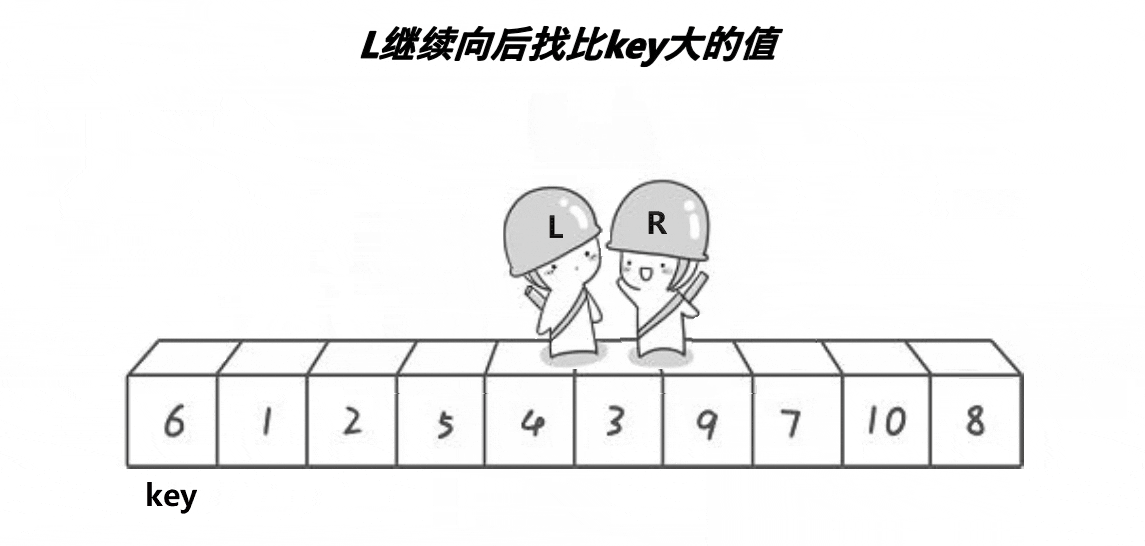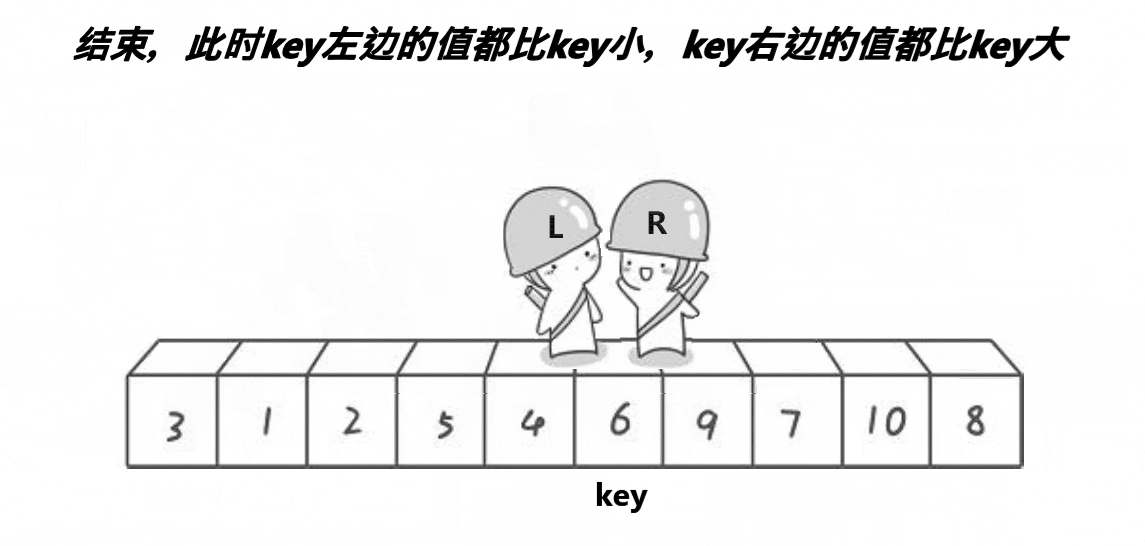
我们可以看到霍尔大佬的排序方法有很多坑的，首先我们是右边开始先找，右边是找小，找到小的时候，停下来，然后就是我们左边开始动，左边是找到到，找到大的时候就开始交换左边和右边，然后再开始我们右边开始找大，左边开始找小，我们这里还是需要注意的就是我们这个排序什么时候才是结束的时候，我们就是条件通过动图可以看到就是right和left相遇的时候，然后这个时候我们需要做的就是交换key和left和rigth相遇地方的值。

这里的唯一难处就是我们为什么他们相遇的时候这个值一定是比key小的？？？

我们left和right相遇有两种情况，一种是right与left相遇，一种是left和right相遇，这两种相遇都是能够确保我们遇到的值是比key小的，我们可以这样来看，第一种情况，right动，left不动，我们的right是找小，?当right遇到left的时候，left的位置肯定是小于key的，我们上一次交换的时候，就是把left变成小的，所以这样也就确保right和left相遇的时候，是比key小的，我们再来看第二种情况就是left去遇到right，因为right是找到小的值，然后我们left去找大，一直没找到大的时候就是到right这个时候条件也不满足了，所以这样left和right碰到时候，条件也是比key小。

但是这个都是因为我们是右边开始先找小的，然后左边开始找大的，如果没有这个条件的话，我们是无法成立left和right相遇的时候值是比key小的。

代码如下

void Swap(int* p1, int* p2)
{
	int tmp = *p1;
	*p1 = *p2;
	*p2 = tmp;
}
int SortPart1(int* a, int left, int right)
{
	int key = a[left];
	int begin = left;
	while (left < right)
	{
		while (left < right && a[right] >= key)
		{
			right--;
		}
		while (left < right && a[left] <= key)
		{
			left++;
		}
		Swap(&a[left], &a[right]);
	}
	Swap(&a[left], &a[begin]);
	return left;
}



void QuickSort(int* a, int begin, int end)
{
	if (begin >= end)
	{
		return;
	}
	int midi = Midi(a, begin, end);
	Swap(&a[begin], &a[midi]);

	int keyi = SortPart3(a, begin, end);
	QuickSort(a, begin, keyi - 1);
	QuickSort(a, keyi+1, end);

}

这样就是我们霍尔大佬的思路，但是霍尔大佬的写法坑是太对了，大家可以看我们的代码是很容易写错的，那我们来看看其他的版本，再看其他版本的时候我们可以优化我们的代码就是我们的三数取中，因为我们的代码逆序的时候是最慢的，所以我们每次取值的时候如果我们的值每次不是最大和最小就很好的解决了我们的这个问题，下面是三数取中的代码。

int Midi(int* a, int left, int right)
{
	int mid = (left + right) / 2;
	if (a[mid] > a[left])
	{
		if (a[right] > a[mid])
		{
			return mid;
		}
		else if (a[right] < a[left])
		{
			return left;
		}
		else
		{
			return right;
		}
	}
	else//left > mid
	{
		if (a[right] > a[left])
		{
			return left;
		}
		else if (a[right] < a[mid])
		{
			return mid;
		}
		else
		{
			return right;
		}
	}
}

我们来看看挖空法的动图。

我们先给出代码，然后对着代码和图来看，让大家更好的理解挖空法。

int Midi(int* a, int left, int right)
{
	int mid = (left + right) / 2;
	if (a[mid] > a[left])
	{
		if (a[right] > a[mid])
		{
			return mid;
		}
		else if (a[right] < a[left])
		{
			return left;
		}
		else
		{
			return right;
		}
	}
	else//left > mid
	{
		if (a[right] > a[left])
		{
			return left;
		}
		else if (a[right] < a[mid])
		{
			return mid;
		}
		else
		{
			return right;
		}
	}
}

void Swap(int* p1, int* p2)
{
	int tmp = *p1;
	*p1 = *p2;
	*p2 = tmp;
}


int SortPart2(int* a, int left, int right)
{
	int hole = left;
	int key = a[hole];
	while (left < right)
	{
		while (left < right && a[right] >= key)
		{
			right--;
		}
		a[hole] = a[right];
		hole = right;
		while (left < right && a[left] <= key)
		{
			left++;
		}
		a[hole] = a[left];
		hole = left;
	}
	a[hole] = key;
	return hole;
}


void QuickSort(int* a, int begin, int end)
{
	if (begin >= end)
	{
		return;
	}
	int midi = Midi(a, begin, end);
	Swap(&a[begin], &a[midi]);

	int keyi = SortPart3(a, begin, end);
	QuickSort(a, begin, keyi - 1);
	QuickSort(a, keyi+1, end);

}

?挖空法的思路其实和霍尔大佬的思想很相似，我们首先一定要保存坑位的数据，因为等等这个数据想当于要被挖空，是个空位，我们记住这个hole是坑位的下标，然后就是key是这个坑位的值，我们先是右边开始找小的，找到小的把这个位置填到到hole那个坑位里，然后就是当前right位置就是新的坑位，左边开始找大，找到大的时候就是再和右边一样，我们把右边的坑位拿左边的值填上，再来左边挖坑，最后left和right遇到的时候就是结束的时候。结束的时候就是最后的坑位，最后的坑位补上我们刚开始的时候的值。

下一个就是我们的前后指针法

我们还是先来看看我们的动图。

前后指针法的我觉得看图就是能够写出代码的，就是cur再找小，找到小的时候，pre要先++然后再次进行交换就行了，cur到最后结束，所以结束条件就是cur <= end我们的代码可以优化成下面的这个代码。?

int Midi(int* a, int left, int right)
{
	int mid = (left + right) / 2;
	if (a[mid] > a[left])
	{
		if (a[right] > a[mid])
		{
			return mid;
		}
		else if (a[right] < a[left])
		{
			return left;
		}
		else
		{
			return right;
		}
	}
	else//left > mid
	{
		if (a[right] > a[left])
		{
			return left;
		}
		else if (a[right] < a[mid])
		{
			return mid;
		}
		else
		{
			return right;
		}
	}
}
void Swap(int* p1, int* p2)
{
	int tmp = *p1;
	*p1 = *p2;
	*p2 = tmp;
}


int SortPart3(int* a, int left, int right)
{
	int pre = left;
	int cur = left + 1;
	int begin = left;
	int end = right;
	while (cur <= end)
	{
		if (a[cur] < a[begin] && ++pre != cur)
		{
			Swap(&a[cur], &a[pre]);
		}
		cur++;
	}
	Swap(&a[pre], &a[begin]);
	return pre;
}
void QuickSort(int* a, int begin, int end)
{
	if (begin >= end)
	{
		return;
	}
	int midi = Midi(a, begin, end);
	Swap(&a[begin], &a[midi]);

	int keyi = SortPart3(a, begin, end);
	QuickSort(a, begin, keyi - 1);
	QuickSort(a, keyi+1, end);

}

那这样我们的前后指针法也是完成了，这三种方法都是递归的方法吗，现在下面来讲讲我们的非递归的方法，非递归的方法首先是要有个栈的，我们先得有个栈，以前的文章有·栈吗，大家也可以用我这个现场简略版的栈。

#include<stdio.h>
#include<assert.h>
#include<stdlib.h>
#include<stdbool.h>

typedef int STDateType;
typedef struct Stack
{
	STDateType* a;
	int top;
	int capacity;
}ST;


void Init(ST* ps);

void Push(ST* ps, STDateType x);

void Pop(ST* ps);

STDateType Top(ST* ps);

void Dstory(ST* ps);

bool Empty(ST* ps);

int Size(ST* ps);


#include"stack.h"


void Init(ST* ps)
{
	assert(ps);
	ps->a = NULL;
	ps->capacity = 0;
	ps->top = -1;
}

void Push(ST* ps, STDateType x)
{
	assert(ps);
	if (ps->top + 1 == ps->capacity)
	{
		int newcapacity = ps->capacity == 0 ? 4 : ps->capacity * 2;
		STDateType* tmp =(STDateType*) realloc(ps->a, sizeof(STDateType) * newcapacity);
		if (tmp == NULL)
		{
			perror("realloc fail");
			exit(-1);
		}
		ps->capacity = newcapacity;
		ps->a = tmp;
	}
	ps->top++;

	ps->a[ps->top] = x;
}


void Pop(ST* ps)
{
	assert(ps);
	assert(ps->top >= 0);
	ps->top--;
}


void Dstory(ST* ps)
{
	assert(ps);
	free(ps->a);
	ps->a = NULL;
	ps->capacity = ps->capacity = 0;
}

STDateType Top(ST* ps)
{
	assert(ps);
	return ps->a[ps->top];
}


bool Empty(ST* ps)
{
	assert(ps);
	return ps->top == -1;
}




int Size(ST* ps)
{
	assert(ps);
	return ps->top + 1;
}

有了这个栈之后我们的非递归的思路其实就是边界问题，我们的栈存储的不是我们数组的值，而是我们每次的begin和end这些下标的值，我们一开始push的值肯定是0和end，我们也一定要注意push的顺序，然后再取出来left和right。我们来看看这个图，例子是这个数组。

我们的代码就是下面的这个。

//非递归
void QuickSortNonR(int* a, int n)
{
	int begin = 0;
	int end = n - 1;
	ST st;
	Init(&st);
	Push(&st, end);
	Push(&st, begin);
	while (!Empty(&st))
	{

		int left = Top(&st);
		Pop(&st);
		int right = Top(&st);
		Pop(&st);
		int keyi = SortPart3(a, left, right);

		if (left < keyi - 1)
		{
			Push(&st, keyi-1);
			Push(&st, left);
		}
		if (right > keyi + 1)
		{
			Push(&st, right);
			Push(&st, keyi+1);
		}
		
	}
	Dstory(&st);
}

?今天分享的就是我们八大排序的快速排序，快速排序是很重要的一个排序，还有一个快速排序还是可以针对我们的很多重复值的排序，比如一堆222222这些种，我们放在后面的OJ题里面来讲他，下一个分享的就是归并排序。我们下次再见。