高精度算法--大数加法

场景引入

在C++中不同类型的变量都有不同的存储范围

例如：

类型	字节	范围
char	1	-2^7~2^7-1
int	4	-2^31~2^31-1
long long	8	-2^63~2^63-1

其中我们可以看到 long long 的存储范围已经相当大了，但是在数位上最多只有19位

这时便产生了一个问题：如何存储大于19位的数呢？

此时就需要使用?高精度算法?来解决问题

?原理

?高精度算法的原理其实类似于小学数学中学到的竖式计算?

?举个栗子：

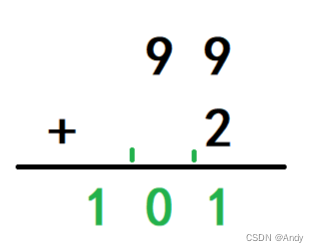
首先计算两个数的个位数 9+2 = 11，保留个位的 1，满 10 进 1

其次计算十位， 9 + 1 = 10，保留个位的 0，满 10 进 1

最后计算百位，保留 1

所以得数就是 101?

高精度算法便是通过代码将这一过程进行模拟?

代码实现

创建变量?

1. 创建两个字符串用于输入加数
2. 创建三个数组分别用于储存加数和得数
3. 创建循环变量

?注：数组的大小一定要足够大，例如加数是200位，那么数组大小可以是210

string s1, s2;//两个加数
int a1[110], a2[110], a3[110] = { 0 };//a1 a2 用于储存两个加数，a3 用于储存得数
int i,len;

?储存加数

1. 将加数输入字符串（这里用到的是getline函数）
2. 使用两个for循环将字符串倒序储存在数组

注：

?????1.（此例中）数组的下标是从后往前移动，字符串的下标是从前往后移动

?????2.字符串储存的是字符，所以在储存到数组时要减字符0才能得到对应的数字?

getline(cin, s1);
getline(cin, s2);

for (i = 0; i < s1.size(); i++)//将 s1 倒序储存在 a1
{
	a1[s1.size()-i - 1] = s1[i] - '0';
}
for (i = 0; i < s2.size(); i++)//将 s2 倒序储存在 a2
{
	a2[s2.size()-i - 1] = s2[i] - '0';
}

模拟竖式计算?

1. ?循环的次数取决于两者间最大的数位，此例中用max函数得到最大值赋值给len
2. 第一个循环，两个加数对应的数位相加
3. 第二个循环，模拟10进制的进位

注：模拟进位时，进1和保留个位两个步骤顺序不能写反?

len = max(s1.size(), s2.size());//得到两个加数中最大的位数

for (i = 0; i < len; i++)//循环len次将a1 a2按数位相加
{
	a3[i] = a1[i] + a2[i];
}
for (i = 0; i < len; i++)//模拟十进制的进位
{
	if (a3[i] >= 10)//满10
	{
		a3[i + 1] = a3[i + 1] + a3[i] / 10;//下一位进1
		a3[i] %= 10;//保留个位数
	}
}

?调整循环变量

这一步非常重要，得数的位数不一定与加数的最大位数相同

如上文的例子中，得数是3位数，但是两个加数最大是2位数

所以需要进行一步判定

a3已经进行了初始化，所以没有被更改的元素都是0

利用这一点我们可以在下标len处判断此元素是否为0，如果不为0，说明最高位有进位，此时len++

if (a3[len] != 0)//如果得数的数位大于两个加数的数位
{
	len++;//更新len的值
}

?输出得数

因为加数是逆序储存的，所以在输出时需要再一次逆序，得到正确的结果

for (i = len-1; i >= 0; i--)//将得数逆序输出
{
	cout << a3[i];
}

?完整代码

#include <iostream>
#include <string>
using namespace std;

int main()
{
	string s1, s2;//两个加数
	int a1[110], a2[110], a3[110] = { 0 };//a1 a2 用于储存两个加数，a3 用于模拟计算
	int i;
	int len;

	getline(cin, s1);
	getline(cin, s2);

	for (i = 0; i < s1.size(); i++)//将 s1 倒序储存在 a1
	{
		a1[s1.size()-i - 1] = s1[i] - '0';
	}
	for (i = 0; i < s2.size(); i++)//将 s2 倒序储存在 a2
	{
		a2[s2.size()-i - 1] = s2[i] - '0';
	}

	len = max(s1.size(), s2.size());//得到两个加数中最大的位数

	for (i = 0; i < len; i++)//循环len次将a1 a2按数位相加
	{
		a3[i] = a1[i] + a2[i];
	}
	for (i = 0; i < len; i++)//模拟十进制的进位
	{
		if (a3[i] >= 10)//若这一位满10
		{
			a3[i + 1] = a3[i + 1] + a3[i] / 10;//下一位进一
			a3[i] %= 10;//当前位数取模得到个位数
		}
	}
	if (a3[len] != 0)//如果得数的数位大于两个加数的数位
	{
		len++;//更新len的值
	}

	for (i = len-1; i >= 0; i--)//将得数逆序输出
	{
		cout << a3[i];
	}
	
    return 0;
}

如果文章内容有误，欢迎指出?