聚类算法之Kmeans聚类详解

聚类算法是无监督学习算法，它根据样本之间的相似性，将样本划分到不同的类别中；不同的相似度计算方法，会得到不同的聚类结果，常用的相似度计算方法有欧氏距离法。聚类算法的目的是在没有先验知识的情况下，自动发现数据集中的内在结构和模式。

聚类算法的分类：

• 按照聚类细粒度分类：细聚类和粗聚类

• 

• 根据实现方法分类：

  • K-means：按照质心分类，主要介绍K-means，通用、普遍

  • 层次聚类：对数据进行逐层划分，直到达到聚类的类别个数

  • DBSCAN聚类：基于密度的聚类算法

  • 谱聚类：基于图论的聚类算法

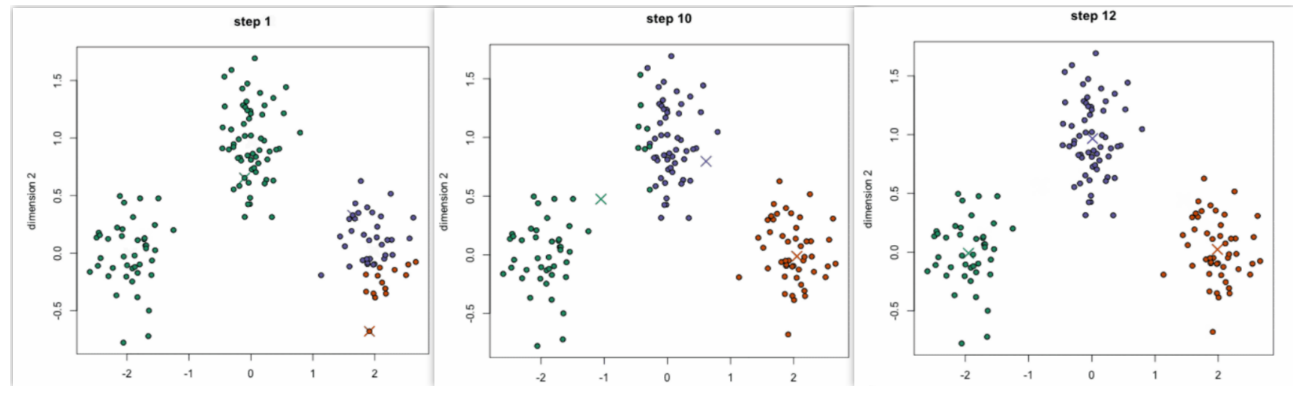
KMeans基本思路

通过计算相似度（默认欧氏距离），将相似度大的样本聚集到同一个类别，K表示聚成K个类别，means表示每个类别的聚类中心点是通过簇中所有样本点的均值得到。

KMeans算法流程：

• 事先确定常数K，K是最终的聚类类别数

• 随机选择K个样本点作为初始的聚类中心

• 计算每个样本点到K个中心点的距离，选择最近的聚类中心点作为标记类别

• 根据分好的类别，计算每个类别的新的聚类中心点（每个点的坐标的平均值），如果得到了新的聚类中心点则停止聚类，否则继续执行第3步，直到聚类中心点不再变化

?

评估方法：

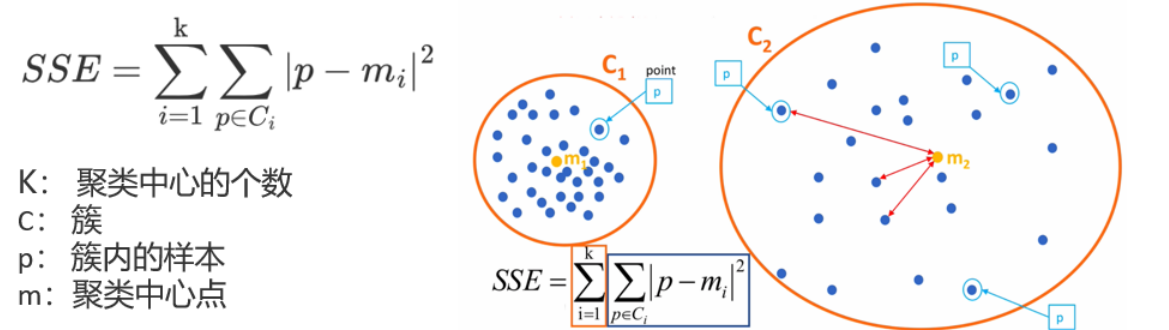
• 误差平方和SSE，值越小，表示数据点越接近它们的中心点，聚类效果越好

• 

• “肘”方法(Elbow method)，通过SSE确定n_clusters的值(K值)

  • 对于n个点的数据集，迭代计算 k from 1 to n，每次聚类完成后计算 SSE

  • 随着类别的增加，SSE 是会逐渐变小的，因为每个点都是它所在的簇中心本身

  • SSE 变化过程中会出现一个拐点，下降率突然变缓时即认为是最佳 n_clusters 值

  • 在决定什么时候停止训练时，肘方法同样有效，数据通常存在噪音，在增加分类无法带来更多回报时，则停止增加类别

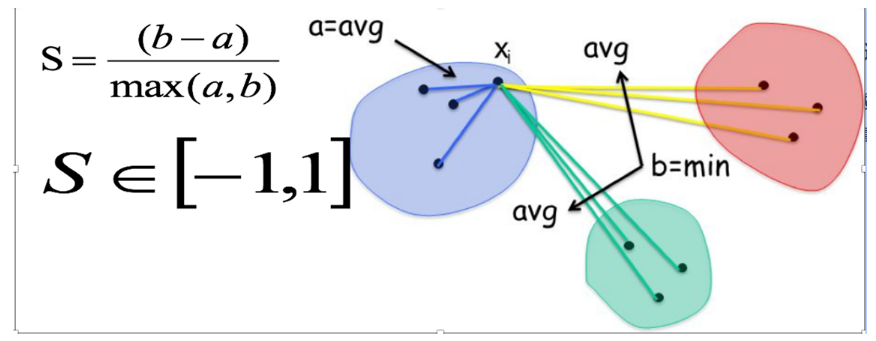
• 轮廓系数法SC(Silhouette Coefficient)，考虑簇内的内聚程度，簇外的分离程度

  • 对每个样本点计算到簇内其它所有样本的平均距离a，值越小，说明簇内聚程度越高

  • 对每个样本点计算到其它簇所有样本的平均距离b，值越大，说明该样本离其它簇越远

  • 计算公式：S = (b - a) / max(a, b)，取值范围为【-1，1】，值越大越好

  • 计算所有样本的平均轮廓系数

  • 

?

from sklearn.datasets import make_blobs  # 加载数据集
from sklearn.cluster import KMeans
from sklearn.metrics import silhouette_score # sc系数 对聚类进行评估
import matplotlib.pyplot as plt
import pandas as pd

customer = pd.read_csv('customers.csv')
customer.describe()  # 做聚类的时候，需要注意特征的取值大小(量纲) 取值差异大需要做归一化/标准化
x = customer.iloc[:,[3,4]]  # 选取第3列和第4列
sse_list = []
sc_score = []
# 先找到最佳的K取值
for k in range(2,11):
    my_kmeans = KMeans(n_clusters=k)
    y_pred = my_kmeans.fit_predict(x)
    sse_list.append(my_kmeans.inertia_)  # kmeans.inertia_ 这个属性表示sse值
    sc_score.append(silhouette_score(x,y_pred))
plt.plot(range(2,11),sse_list)
plt.grid()
plt.title('sse')
plt.show()
plt.plot(range(2,11),sc_score)
plt.grid()
plt.title('sc_score')
plt.show()
# 从以上绘图中，找到sse的拐点和sc_score的最高点，图像显示为n_clusters=5时候最好
kmeans = KMeans(n_clusters=5)
y_pred= kmeans.fit_predict(X)
customer['cluster'] = y_pred  # 将聚类结果加到数据表中

?