Unity中URP下深度图的线性转化
文章目录
前言
在之前的文章中,我们实现了对深度图的使用。因为,深度图不是线性的。所以,在使用时,我们使用了 Linear01Depth 函数对其进行了线性转化。
但是,对深度图进行线性转化 还有其他函数。
在这篇文章中,我们来看一下深度图线性转化的 Linear01Depth函数 和 LinearEyeDepth 函数 干了什么。
一、_ZBufferParams参数有两组值
-
在OpenGL下

-
在类DirectX下
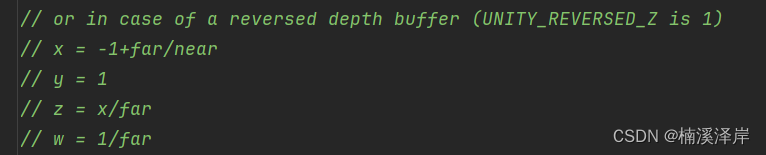
二、LinearEyeDepth
1、使用
-
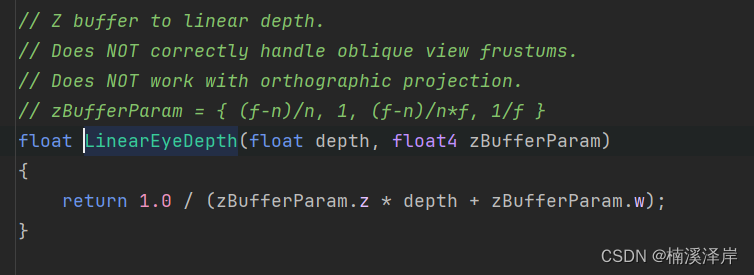
对采样的深度图纹理进行线性转化
-
转化后的值,就是原来物体的深度 Z 值
float4 cameraDepthTex = SAMPLE_TEXTURE2D(_CameraDepthTexture,sampler_CameraDepthTexture,uv);
float depthTex = LinearEyeDepth(cameraDepthTex,_ZBufferParams);
- 返回结果全白,效果不明显

- 我们对其取小数部分,使其效果明显一点
frac(depthTex)

2、Unity源码推导:
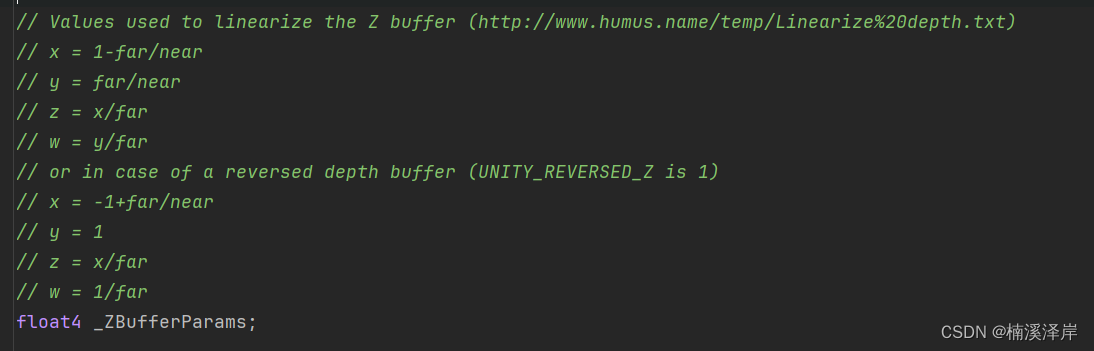
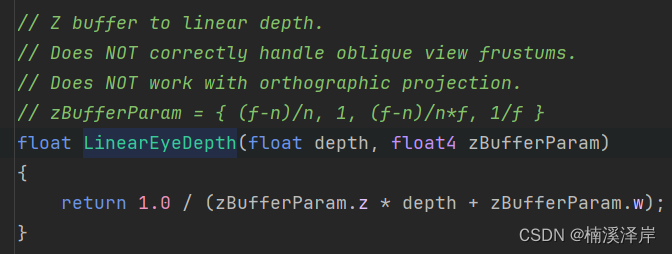
- 这里使用OpenGL下推导
Z v i e w = 1 1 ? f n f d + f n f Z_{view}=\frac{1}{\frac{1-\frac{f}{n}}{f}d+\frac{\frac{f}{n}}{f}} Zview?=f1?nf??d+fnf??1?
Z v i e w = 1 ( n n ? f n ) 1 f d + 1 n Z_{view}=\frac{1}{(\frac{n}{n}-\frac{f}{n})\frac{1}{f}d+\frac{1}{n}} Zview?=(nn??nf?)f1?d+n1?1?
Z v i e w = 1 ( n ? f n ) 1 f d + 1 n Z_{view}=\frac{1}{(\frac{n-f}{n})\frac{1}{f}d+\frac{1}{n}} Zview?=(nn?f?)f1?d+n1?1?
Z v i e w = 1 n ? f n f d + 1 n Z_{view}=\frac{1}{\frac{n-f}{nf}d+\frac{1}{n}} Zview?=nfn?f?d+n1?1?
3、使用矩阵推导:
-
OpenGL
[ 2 n w 0 0 0 0 2 n h 0 0 0 0 n + f n ? f 2 n f n ? f 0 0 ? 1 0 ] \begin{bmatrix} \frac{2n}{w} & 0 & 0 & 0 \\ 0 & \frac{2n}{h} & 0 &0\\ 0 & 0 & \frac{n+f}{n-f} &\frac{2nf}{n-f}\\ 0 & 0 & -1 & 0\\ \end{bmatrix} ?w2n?000?0h2n?00?00n?fn+f??1?00n?f2nf?0? ? -
DirectX
[ 2 n w 0 0 0 0 2 n h 0 0 0 0 n f ? n n f f ? n 0 0 ? 1 0 ] \begin{bmatrix} \frac{2n}{w} & 0 & 0 & 0 \\ 0 & \frac{2n}{h} & 0 &0\\ 0 & 0 & \frac{n}{f-n} &\frac{nf}{f-n}\\ 0 & 0 & -1 & 0\\ \end{bmatrix} ?w2n?000?0h2n?00?00f?nn??1?00f?nnf?0? ? -
由观察空间转化到裁剪空间矩阵可得
Z c l i p = n + f n ? f Z v i e w + 2 n f n ? f W v i e w Z_{clip}=\frac{n+f}{n-f}Z_{view}+\frac{2nf}{n-f}W_{view} Zclip?=n?fn+f?Zview?+n?f2nf?Wview?
W c l i p = ? Z v i e w W_{clip}=-Z_{view} Wclip?=?Zview? -
做透视除法可得
Z n d c = Z c l i p W c l i p = n + f n ? f Z v i e w + 2 n f n ? f ? Z v i e w = n + f f ? n + 2 n f ( f ? n ) Z v i e w Z_{ndc} = \frac{Z_{clip}}{W_{clip}} = \frac{\frac{n+f}{n-f}Z_{view}+\frac{2nf}{n-f}}{-Z_{view}}=\frac{n+f}{f-n}+\frac{2nf}{(f-n)Z_{view}} Zndc?=Wclip?Zclip??=?Zview?n?fn+f?Zview?+n?f2nf??=f?nn+f?+(f?n)Zview?2nf? -
d = 0.5 ? Z n d c + 0.5 d=0.5·Z_{ndc}+0.5 d=0.5?Zndc?+0.5
d = 0.5 ? ( n + f f ? n + 2 n f ( f ? n ) Z v i e w ) + 0.5 d = 0.5·(\frac{n+f}{f-n}+\frac{2nf}{(f-n)Z_{view}})+0.5 d=0.5?(f?nn+f?+(f?n)Zview?2nf?)+0.5 -
我们由 d d d 公式化简,即可得到 Z v i e w Z_{view} Zview?
Z v i e w = 1 f ? n n f d ? 1 n Z_{view} = \frac{1}{\frac{f-n}{nf}d-\frac{1}{n}} Zview?=nff?n?d?n1?1? -
为了得到正的Z值,需要取反
Z v i e w = ? 1 f ? n n f d ? 1 n Z_{view} =- \frac{1}{\frac{f-n}{nf}d-\frac{1}{n}} Zview?=?nff?n?d?n1?1?
Z v i e w = 1 n ? f n f d + 1 n Z_{view}=\frac{1}{\frac{n-f}{nf}d+\frac{1}{n}} Zview?=nfn?f?d+n1?1?
三、Linear01Depth
1、使用
-
对采样的深度图纹理进行线性转化
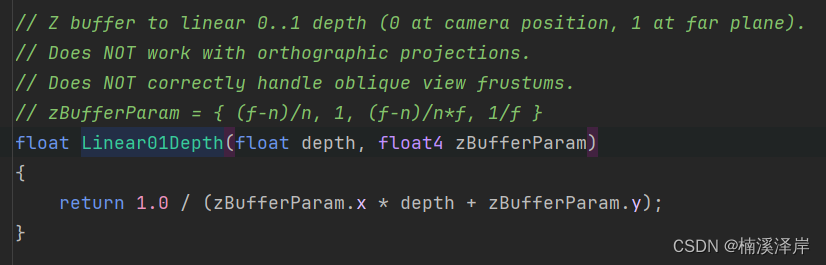
-
转化后的值,是Z值在[0,1]区间的值
float4 cameraDepthTex = SAMPLE_TEXTURE2D(_CameraDepthTexture,sampler_CameraDepthTexture,uv);
float depthTex = Linear01Depth(cameraDepthTex,_ZBufferParams);
- 返回结果

2、Unity源码推导
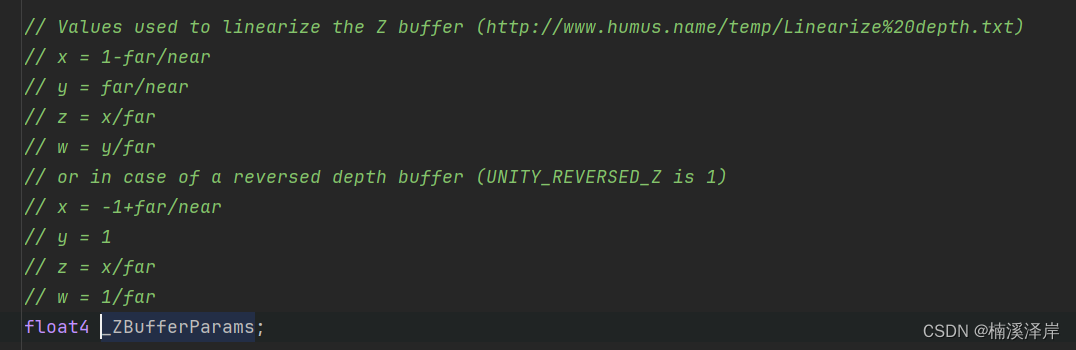
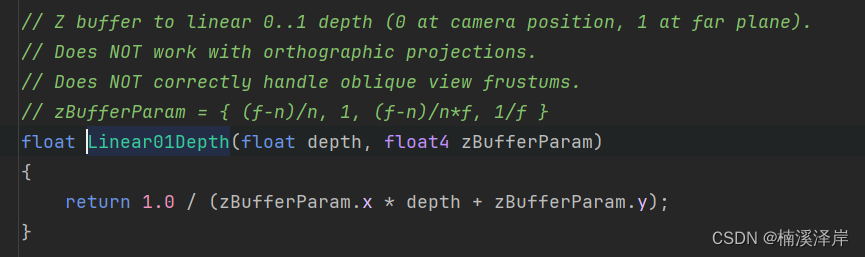
- OpenGL下推导:
Z v i e w = 1 ( 1 ? f n ) d + f n Z_{view}= \frac{1}{(1-\frac{f}{n})d+\frac{f}{n}} Zview?=(1?nf?)d+nf?1?
3、数学推导:
-
这是LinearEyeDepth下推导出来的
Z v i e w = 1 n ? f n f d + 1 n Z_{view}=\frac{1}{\frac{n-f}{nf}d+\frac{1}{n}} Zview?=nfn?f?d+n1?1? -
Z v i e w Z_{view} Zview?的取值范围 [ n e a r , f a r ] [near,far] [near,far]
-
使其除以一个 f f f得到 Linear01Depth函数的结果
Z v i e w = 1 n ? f n f d + 1 n ? 1 f = 1 n ? f n f d f + f n = 1 ( 1 ? f n ) d + f n Z_{view}=\frac{1}{\frac{n-f}{nf}d+\frac{1}{n}}·\frac{1}{f}=\frac{1}{\frac{n-f}{nf}df+\frac{f}{n}}=\frac{1}{(1-\frac{f}{n})d+\frac{f}{n}} Zview?=nfn?f?d+n1?1??f1?=nfn?f?df+nf?1?=(1?nf?)d+nf?1?
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
- Python教程
- 深入理解 MySQL 中的 HAVING 关键字和聚合函数
- Qt之QChar编码(1)
- MyBatis入门基础篇
- 用Python脚本实现FFmpeg批量转换
- 【工具栏】RestfulTool 插件的使用(接口开发规范)
- Java面向对象(抽象类,接口,内部类)
- CentOS 7.6下的HTTP隧道代理配置详解
- Azkaban+Spark资源调度
- 【字典树Trie】LeetCode-139. 单词拆分
- 华纳云:ServiceComb如何实现zipkin分布式调用链追踪
- CIDR标记法计算网络号、主机号、子网掩码
- Linux关闭Swap交换分区的优点和缺点
- 排序算法7----归并排序(C语言)
- 2024年【施工升降机司机(建筑特殊工种)】考试总结及施工升降机司机(建筑特殊工种)操作证考试