Java解决不同路径问题
发布时间:2023年12月17日
Java解决不同路径问题
01 题目
一个机器人位于一个 m x n 网格的左上角 (起始点在下图中标记为 “Start” )。
机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角(在下图中标记为 “Finish” )。
问总共有多少条不同的路径?
示例 1:
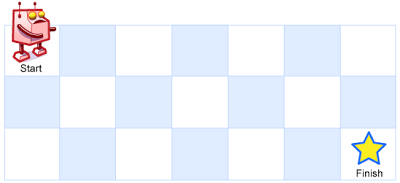
输入:m = 3, n = 7
输出:28
示例 2:
输入:m = 3, n = 2
输出:3
解释:
从左上角开始,总共有 3 条路径可以到达右下角。
1. 向右 -> 向下 -> 向下
2. 向下 -> 向下 -> 向右
3. 向下 -> 向右 -> 向下
示例 3:
输入:m = 7, n = 3
输出:28
示例 4:
输入:m = 3, n = 3
输出:6
提示:
1 <= m, n <= 100- 题目数据保证答案小于等于
2 * 109
02 知识点
- 二维数组
- DP(动态规划)
03 我的题解
public class digui01 {
public static void main(String[] args) {
//测试数据
uniquePaths(3, 7);
}
public static int uniquePaths(int m, int n) {
//通过二维数组来记录每个各格子的路径值
//路径值指到这个格子的方法数
int[][] grid=new int[m][n];
//因为每次出发一定会经过第一行或第一列某一格,所以设第一行和第一列格子上的值为1
for (int i = 0; i < m; i++) {
grid[i][0]=1;
}
for (int j= 0; j < n; j++) {
grid[0][j]=1;
}
//因为进入中间的格子只能从上方或者左边,所以中间格子的路径值为二者之和
for (int i = 1; i < grid.length; i++) {
for (int j = 1; j < grid[0].length; j++) {
grid[i][j]=grid[i-1][j]+grid[i][j-1];
}
}
//返回值为左下角的路径值
return grid[m-1][n-1];
}
}
文章来源:https://blog.csdn.net/2302_77182979/article/details/135037447
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
最新文章
- Python教程
- 深入理解 MySQL 中的 HAVING 关键字和聚合函数
- Qt之QChar编码(1)
- MyBatis入门基础篇
- 用Python脚本实现FFmpeg批量转换
- pytest多线程与多设备并发appium
- 开始学习第一天
- facebook广告对于推广的重要性
- 在iPhone或iPad和Windows PC之间复制和粘贴文本的几种方法,总有一种适合你
- Day 37 贪心算法 6
- Neos的渗透测试靶机练习——DarkHole-1
- 【代码随想录算法训练营-第七天】【哈希表】454,383,15,18
- Go后端开发 -- 数组 && slice && map && range
- liunx安装redis
- 12.23C语言 指针