冒泡排序之C++实现
发布时间:2023年12月24日
描述
冒泡排序算法是一种简单的排序算法,它通过将相邻的元素进行比较并交换位置来实现排序。冒泡排序的基本思想是,每一轮将未排序部分的最大元素逐个向右移动到已排序部分的最右边,直到所有元素都按照从小到大的顺序排列。
冒泡排序的算法描述如下:
- 从数组的第一个元素开始,依次比较相邻的两个元素,如果前一个元素大于后一个元素,则交换它们的位置。
- 继续比较下一对相邻元素,重复上述步骤,直到比较到数组的倒数第二个元素。
- 重复以上步骤,直到所有元素都按照从小到大的顺序排列。
时间复杂度和空间复杂度
冒泡排序的时间复杂度为O(n^2),其中n是待排序数组的元素个数。冒泡排序的最坏情况和平均情况下,需要比较的次数是n(n-1)/2,即比较轮数为n-1,每轮比较的次数为n-i-1,其中i表示当前轮数。
冒泡排序的空间复杂度为O(1),即不需要额外的空间来存储数组元素。冒泡排序是在原地进行排序,只是通过交换相邻元素的位置来实现排序,所以只需要常量级的额外空间。
图解
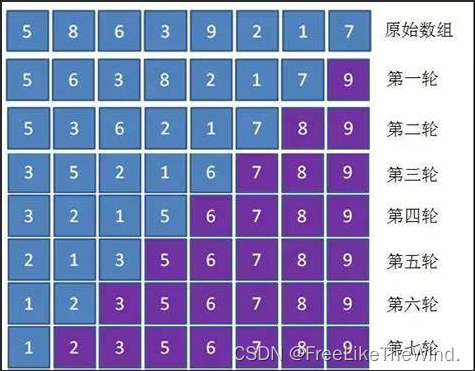
示例
#include <iostream>
using namespace std;
void bubbleSort(int arr[], int n) {
for (int i = 0; i < n-1; i++) {
for (int j = 0; j < n-i-1; j++) {
if (arr[j] > arr[j+1]) {
swap(arr[j], arr[j+1]);
}
}
}
}
int main() {
int arr[] = {64, 34, 25, 12, 22, 11, 90};
int n = sizeof(arr)/sizeof(arr[0]);
bubbleSort(arr, n);
cout << "冒泡排序: \n";
for (int i=0; i < n; i++) {
cout << arr[i] << " ";
}
cout << endl;
return 0;
}
输出结果为:
冒泡排序:
11 12 22 25 34 64 90
冒泡排序优缺点
优点:
- 简单易懂:冒泡排序是最简单的排序算法之一,容易实现和理解。
- 不需要额外空间:冒泡排序是在原地进行排序,不需要额外的空间来存储排序结果。
- 稳定性:冒泡排序是稳定的排序算法,即相等元素的相对顺序不会改变。
缺点:
- 效率较低:冒泡排序的时间复杂度为O(n^2),在大规模数据的情况下,性能较差,特别是与其他高效排序算法相比。
- 不适用于大规模数据:由于冒泡排序的时间复杂度较高,对于大规模数据的排序不适合使用。
- 不适合逆序情况:对于已经基本有序或者逆序的数据,冒泡排序的交换操作较多,效率低下。
冒泡排序技巧
-
冒泡排序的核心思想是相邻元素比较交换,可以通过设置一个标志位来记录是否进行了交换,如果一次遍历没有进行交换,说明数组已经有序,可以提前退出排序。
-
外层循环控制比较的次数,内层循环控制每次比较的元素。
-
在每次内层循环中,可以通过设置一个标志位来记录是否有交换发生,如果没有,说明数组已经有序,可以提前退出内层循环。
-
冒泡排序可以进行优化,每次内层循环比较时,可以将最大(或最小)的元素冒泡到数组的末尾(或开头),使得下一次循环中只需比较剩下的元素。
-
可以使用双层循环来实现冒泡排序,也可以使用递归的方式来实现。
-
冒泡排序适用于小规模的数据排序,对于大规模数据或者时间敏感的场景,建议使用其他更高效的排序算法。
结论
且听且忘且随风,且行且看且从容
文章来源:https://blog.csdn.net/MrHHHHHH/article/details/135176503
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
最新文章
- Python教程
- 深入理解 MySQL 中的 HAVING 关键字和聚合函数
- Qt之QChar编码(1)
- MyBatis入门基础篇
- 用Python脚本实现FFmpeg批量转换
- 光伏设计方案:实现清洁能源的未来
- 电脑控制多台手机的脚本:优势与实现!
- 作业安全风险管控系统在工业生产过程中的应用
- mysql原理--单表访问方法
- SpringBoot运维(一)-- Java程序的打包与运行
- 【方法】如何合并7z分卷压缩文件?
- Java参数校验详解:使用@Valid注解和自定义注解进行参数验证
- Sentinel
- 防火墙设备登录配置实战:掌握这些技巧,安全无忧!
- 树莓派ubuntu:手机蓝牙连接树莓派开发板,取消配对验证操作,自动完成连接