深度学习记录--Momentum gradient descent

Momentum gradient descent

正常的梯度下降无法使用更大的学习率，因为学习率过大可能导致偏离函数范围，这种上下波动导致学习率无法得到提高，速度因此减慢(下图蓝色曲线)

为了减小波动，同时加快速率，可以使用momentum梯度下降：

将指数加权平均运用到梯度下降，成为momentum梯度下降(图中红色曲线)

原理：

纵轴上，平均过程中正负数相互抵消，所以纵轴上的平均值接近于0

横轴上，所有的微分都指向横轴方向，所有横轴方向上的平均值依然较大

因此，纵轴上摆动减小，横轴上运动速度加快

进一步解释：

把图像比作一个碗，轨迹视为小球的轨迹，从边缘向碗内最低点运动

其中dw,db可以看作加速度，v_dw,v_db可以看作速度，可以看作摩擦力

因此，小球会向着碗中心运动，最终因摩擦力而停下来

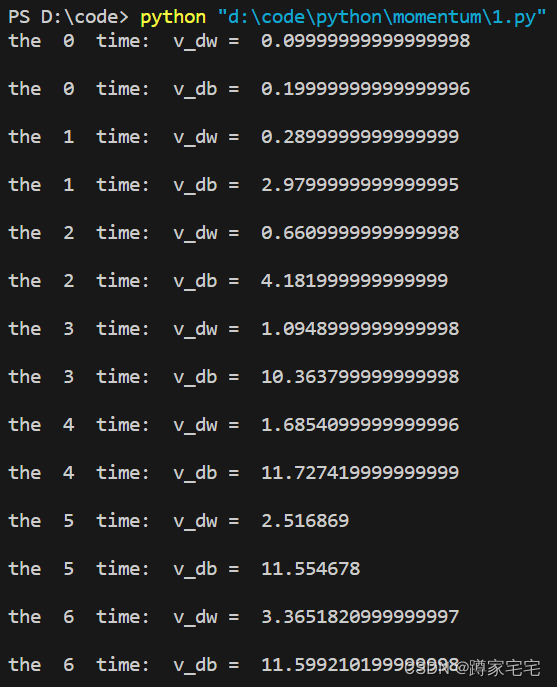
代码演示：

v_dw=0;v_db=0
BETA=0.9
dw=[1,2,4,5,7,10,11]
db=[2,28,15,66,24,10,12]
for i in range(0,7):
    v_dw=BETA*v_dw+(1-BETA)*dw[i]
    v_db=BETA*v_db+(1-BETA)*db[i]
    print("the ",i," time: ","v_dw = ",v_dw,"\n")
    print("the ",i," time: ","v_db = ",v_db,"\n")

结果如下：