机器学习数据的清洗,转化,汇总及建模完整步骤(基于Titanic数据集)
发布时间:2023年12月21日
目录
介绍:?
线性回归是一种常用的机器学习方法,用于建立一个输入变量与输出变量之间线性关系的预测模型。线性回归的目标是找到一条最佳拟合直线,使得预测值与实际观测值之间的误差最小。
线性回归的训练过程是通过最小化目标变量与预测值之间的平方误差来确定模型的参数。常用的最小化目标函数是平方误差和(Sum of Squared Errors,SSE)。
线性回归模型的优点包括简单易懂、计算效率高、可解释性强。然而,线性回归模型的局限性在于假设了输入和输出之间的关系是线性的,无法很好地处理非线性关系。
线性回归模型可以通过添加多项式特征、交互项或者使用其他非线性变换方法来解决非线性问题。此外,还可以使用正则化技术(如岭回归、Lasso回归)来改善模型的泛化能力和抗噪能力。
参考:Logistic Regression逻辑线性回归(基于diabetes数据集)-CSDN博客
Ridge & Lasso Regression解决线性回归的过拟合(Overfitting)(基于波士顿房价预测)-CSDN博客
?Linear Regression线性回归(一元、多元)-CSDN博客
一、数据
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
%matplotlib inline
data=pd.read_csv("Titanic.csv")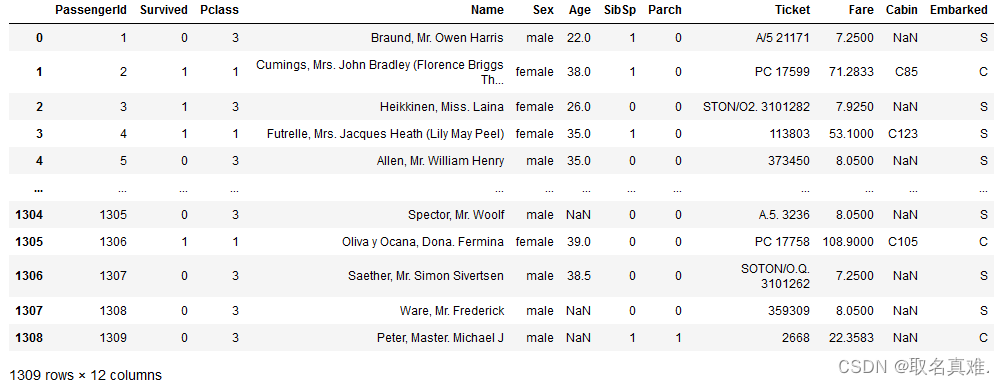
二、检查数据缺失
data.isnull()#true即为缺失,也可以用isna()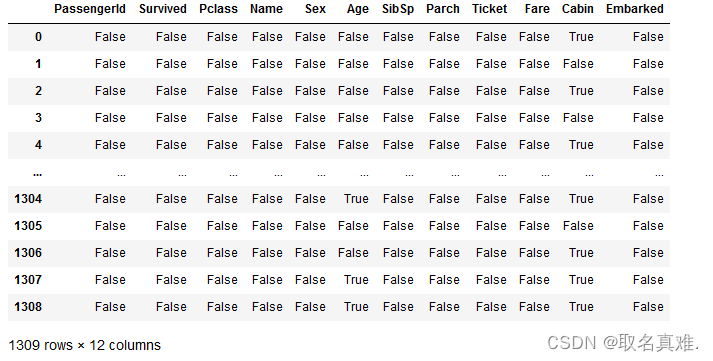
sns.heatmap(data.isnull())#可以看到age和cabin缺失数据比较多?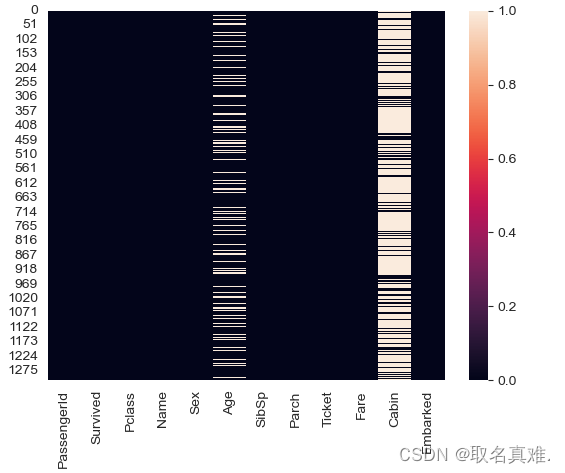
sns.heatmap(data.isnull(),yticklabels=False,cmap='rainbow')?
data['Age'].isnull().sum()
#结果:263
data['Cabin'].isnull().sum()
#结果:1014?三、数据分析
sns.set_style('whitegrid')
sns.countplot(x='Survived',data=data)#死亡的人占大部分
data['Survived'].value_counts()?
sns.set_style('whitegrid')
sns.countplot(x='Survived',hue='Pclass',data=data,palette='rainbow')#再分舱位?
sns.displot(data['Age'],kde=True,color='darkred',bins=40)?
sns.countplot(x='SibSp',data=data)#亲属?
四、数据清洗
plt.figure(figsize=(12,7))
sns.boxplot(x='Pclass',y='Age',data=data)#可以看出舱位和年龄的关系?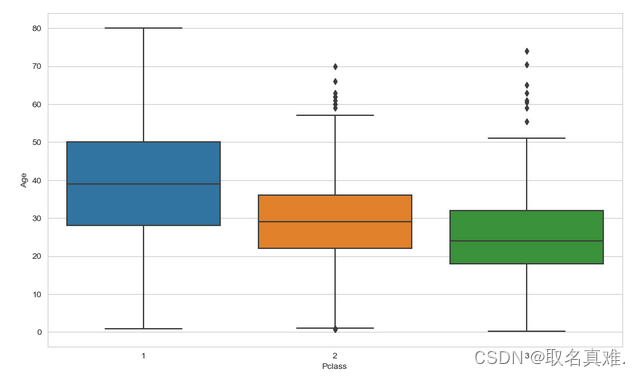
data[data['Pclass']==1]['Age'].median()#每个舱位的平均年龄
#39
data[data['Pclass']==2]['Age'].median()
#29
data[data['Pclass']==3]['Age'].median()
#24
def addage(X):
Age = X[0]
Pclass=X[1]
if pd.isnull(Age):
if Pclass == 1:
return 39
elif Pclass ==2:
return 29
else:
return 24
else:
return Age
data['Age']=data[['Age','Pclass']].apply(addage,axis=1)#赋值给这个函数
data.drop('Cabin',axis=1,inplace=True)#因为船舱房间号缺失严重,删除这列数据
sns.heatmap(data.isnull(),yticklabels=False,cmap='rainbow')#都无缺失数据 ????????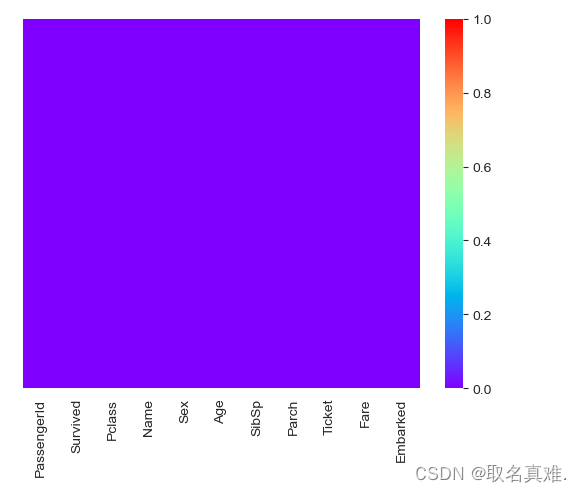
?五、数据类别转化
data.info()##需要转化object类型的数据
'''结果:
<class 'pandas.core.frame.DataFrame'>
RangeIndex: 1309 entries, 0 to 1308
Data columns (total 11 columns):
# Column Non-Null Count Dtype
--- ------ -------------- -----
0 PassengerId 1309 non-null int64
1 Survived 1309 non-null int64
2 Pclass 1309 non-null int64
3 Name 1309 non-null object
4 Sex 1309 non-null object
5 Age 1309 non-null float64
6 SibSp 1309 non-null int64
7 Parch 1309 non-null int64
8 Ticket 1309 non-null object
9 Fare 1308 non-null float64
10 Embarked 1307 non-null object
dtypes: float64(2), int64(5), object(4)
memory usage: 112.6+ KB
'''
data['Embarked'].unique()
#array(['S', 'C', 'Q', nan], dtype=object)
pd.get_dummies(data['Embarked'],drop_first=True)#三个数据,用两个表示即可,00表示C
pd.get_dummies(data['Sex'],drop_first=True)#两个数据,一个表示即可,0表示falme
sex=pd.get_dummies(data['Embarked'],drop_first=True)
embark=pd.get_dummies(data['Sex'],drop_first=True)六、数据汇总和整理
data=pd.concat([data,sex,embark],axis=1)#数据汇总
data.drop(['Sex','Embarked','Name','Ticket'],axis=1,inplace=True)#删除类别数据,无用数据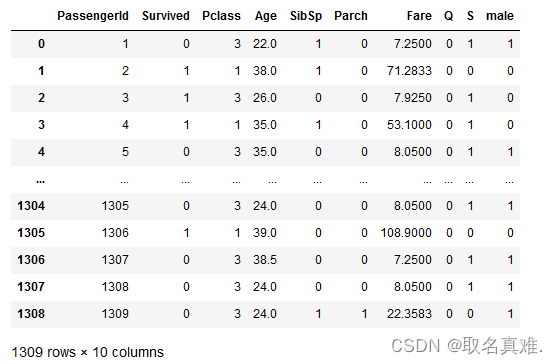
七、建模
#数据清洗完毕,开始建模
#y变量是0,1二分类,用from sklearn.linear_model import LogisticRegression#逻辑线性回归
X=data.drop('Survived',axis=1)
y=data['Survived']
from sklearn.model_selection import train_test_split#将数据分成测试和训练集
X_train,X_test,y_train,y_test=train_test_split(X,y,test_size=0.3,random_state=0)#测试集占百分之三十,random_state=0随机抽取数据集里的成为测试集
from sklearn.linear_model import LogisticRegression
logitmodel = LogisticRegression()
logitmodel.fit(X_train,y_train)
y_predictions= logitmodel.predict(X_test)#预测值
from sklearn.metrics import confusion_matrix
confusion_matrix(y_test,y_predictions)
'''结果:
array([[193, 29],
[ 25, 146]], dtype=int64)
'''
from sklearn.metrics import accuracy_score
accuracy=accuracy_score(y_test,y_predictions)#模型值
#0.8625954198473282
from sklearn.metrics import classification_report
print(classification_report(y_test,y_predictions))
'''结果:
precision recall f1-score support
0 0.89 0.87 0.88 222
1 0.83 0.85 0.84 171
accuracy 0.86 393
macro avg 0.86 0.86 0.86 393
weighted avg 0.86 0.86 0.86 393
?
'''
文章来源:https://blog.csdn.net/qq_74156152/article/details/135119765
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!