LeetCode 每日一题 Day 28&29&30&31 ||三则模拟||找循环节(hard)
1185. 一周中的第几天
给你一个日期,请你设计一个算法来判断它是对应一周中的哪一天。
输入为三个整数:day、month 和 year,分别表示日、月、年。
您返回的结果必须是这几个值中的一个 {“Sunday”, “Monday”, “Tuesday”, “Wednesday”, “Thursday”, “Friday”, “Saturday”}。
示例 1:
输入:day = 31, month = 8, year = 2019
输出:“Saturday”
示例 2:
输入:day = 18, month = 7, year = 1999
输出:“Sunday”
示例 3:
输入:day = 15, month = 8, year = 1993
输出:“Sunday”
提示:
给出的日期一定是在 1971 到 2100 年之间的有效日期。
年底的简单模拟题:
class Solution {
public:
string dayOfTheWeek(int day, int month, int year) {
// 1971年1月1日是星期五
int knownDayOfWeek = 5;
// 月份天数表,注意2月份需要根据闰年来确定天数
int daysInMonth[] = {0, 31, 28, 31, 30, 31, 30, 31, 31, 30, 31, 30, 31};
if ((year % 4 == 0 && year % 100 != 0) || (year % 400 == 0)) {
daysInMonth[2] = 29; // 闰年2月有29天
}
// 累计天数
int totalDays = 0;
for (int y = 1971; y < year; ++y) {
totalDays += 365;
if ((y % 4 == 0 && y % 100 != 0) || (y % 400 == 0)) {
totalDays++; // 闰年多加一天
}
}
for (int m = 1; m < month; ++m) {
totalDays += daysInMonth[m];
}
totalDays += day - 1; // 减去1,因为日期从1开始
// 计算星期几
int dayOfWeek = (knownDayOfWeek + totalDays) % 7;
// 星期几的映射
std::string daysOfWeek[] = {"Friday", "Saturday", "Sunday", "Monday",
"Tuesday", "Wednesday", "Thursday"};
return daysOfWeek[dayOfWeek];
}
};
1154. 一年中的第几天
给你一个字符串 date ,按 YYYY-MM-DD 格式表示一个 现行公元纪年法 日期。返回该日期是当年的第几天。
示例 1:
输入:date = “2019-01-09”
输出:9
解释:给定日期是2019年的第九天。
示例 2:
输入:date = “2019-02-10”
输出:41
提示:
date.length == 10
date[4] == date[7] == ‘-’,其他的 date[i] 都是数字
date 表示的范围从 1900 年 1 月 1 日至 2019 年 12 月 31 日
class Solution {
public:
int dayOfYear(string date) {
int year = stoi(date.substr(0, 4));
int month = stoi(date.substr(5, 2));
int day = stoi(date.substr(8, 2));
int amount[] = {31, 28, 31, 30, 31, 30, 31, 31, 30, 31, 30, 31};
if (year % 400 == 0 || (year % 4 == 0 && year % 100 != 0)) {
++amount[1];
}
int ans = 0;
for (int i = 0; i < month - 1; ++i) {
ans += amount[i];
}
return ans + day;
}
};
该题同样是模拟,掌握stoi的使用即可,当然也可以前缀和解决。
1599. 经营摩天轮的最大利润
你正在经营一座摩天轮,该摩天轮共有 4 个座舱 ,每个座舱 最多可以容纳 4 位游客 。你可以 逆时针 轮转座舱,但每次轮转都需要支付一定的运行成本 runningCost 。摩天轮每次轮转都恰好转动 1 / 4 周。
给你一个长度为 n 的数组 customers , customers[i] 是在第 i 次轮转(下标从 0 开始)之前到达的新游客的数量。这也意味着你必须在新游客到来前轮转 i 次。每位游客在登上离地面最近的座舱前都会支付登舱成本 boardingCost ,一旦该座舱再次抵达地面,他们就会离开座舱结束游玩。
你可以随时停下摩天轮,即便是 在服务所有游客之前 。如果你决定停止运营摩天轮,为了保证所有游客安全着陆,将免费进行所有后续轮转 。注意,如果有超过 4 位游客在等摩天轮,那么只有 4 位游客可以登上摩天轮,其余的需要等待 下一次轮转 。
返回最大化利润所需执行的 最小轮转次数 。 如果不存在利润为正的方案,则返回 -1 。
示例 1:
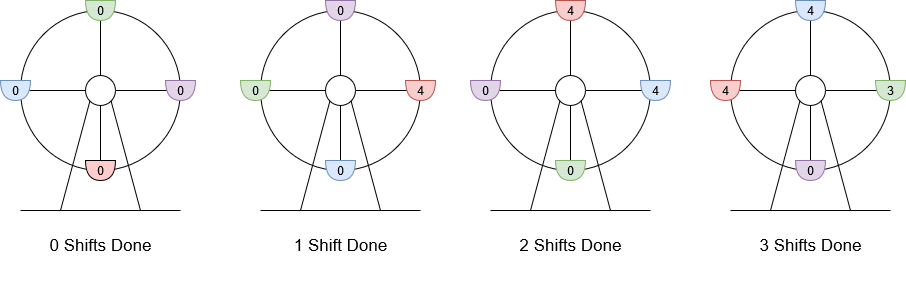
输入:customers = [8,3], boardingCost = 5, runningCost = 6
输出:3
解释:座舱上标注的数字是该座舱的当前游客数。
- 8 位游客抵达,4 位登舱,4 位等待下一舱,摩天轮轮转。当前利润为 4 * $5 - 1 * $6 = $14 。
- 3 位游客抵达,4 位在等待的游客登舱,其他 3 位等待,摩天轮轮转。当前利润为 8 * $5 - 2 * $6 = $28 。
- 最后 3 位游客登舱,摩天轮轮转。当前利润为 11 * $5 - 3 * $6 = $37 。
轮转 3 次得到最大利润,最大利润为 $37 。
示例 2:
输入:customers = [10,9,6], boardingCost = 6, runningCost = 4
输出:7
解释:
- 10 位游客抵达,4 位登舱,6 位等待下一舱,摩天轮轮转。当前利润为 4 * $6 - 1 * $4 = $20 。
- 9 位游客抵达,4 位登舱,11 位等待(2 位是先前就在等待的,9 位新加入等待的),摩天轮轮转。当前利润为 8 * $6 - 2 * $4 = $40 。
- 最后 6 位游客抵达,4 位登舱,13 位等待,摩天轮轮转。当前利润为 12 * $6 - 3 * $4 = $60 。
- 4 位登舱,9 位等待,摩天轮轮转。当前利润为 * $6 - 4 * $4 = $80 。
- 4 位登舱,5 位等待,摩天轮轮转。当前利润为 20 * $6 - 5 * $4 = $100 。
- 4 位登舱,1 位等待,摩天轮轮转。当前利润为 24 * $6 - 6 * $4 = $120 。
- 1 位登舱,摩天轮轮转。当前利润为 25 * $6 - 7 * $4 = $122 。
轮转 7 次得到最大利润,最大利润为$122 。
示例 3:
输入:customers = [3,4,0,5,1], boardingCost = 1, runningCost = 92
输出:-1
解释:
- 3 位游客抵达,3 位登舱,0 位等待,摩天轮轮转。当前利润为 3 * $1 - 1 * $92 = -$89 。
- 4 位游客抵达,4 位登舱,0 位等待,摩天轮轮转。当前利润为 7 * $1 - 2 * $92 = -$177 。
- 0 位游客抵达,0 位登舱,0 位等待,摩天轮轮转。当前利润为 7 * $1 - 3 * $92 = -$269 。
- 5 位游客抵达,4 位登舱,1 位等待,摩天轮轮转。当前利润为 11 * $1 - 4 * $92 = -$357 。
- 1 位游客抵达,2 位登舱,0 位等待,摩天轮轮转。当前利润为 13 * $1 - 5 * $92 = -$447 。
利润永不为正,所以返回 -1 。
提示:
n == customers.length
1 <= n <= 105
0 <= customers[i] <= 50
1 <= boardingCost, runningCost <= 100
题目虽然长,但是逻辑很清晰,我们直接模拟计算即可:
class Solution {
public:
int minOperationsMaxProfit(vector<int>& customers, int boardingCost, int runningCost) {
int ans = -1;
int mx = 0, t = 0;
int wait = 0, i = 0;
while (wait || i < customers.size()) {
wait += i < customers.size() ? customers[i] : 0;
int up = min(4, wait);
wait -= up;
++i;
t += up * boardingCost - runningCost;
if (t > mx) {
mx = t;
ans = i;
}
}
return ans;
}
};
466. 统计重复个数(hard)
这个题实在是不会做,加上这两周在准备考试,草草看了题解就去复习了,等放假后细补:
class Solution {
public:
int getMaxRepetitions(string s1, int n1, string s2, int n2) {
if (n1 == 0)
{
return 0;
}
int ns1 = s1.size();
int ns2 = s2.size();
// s1和s2重复出现的数量
int s1cnt = 0;
int s2cnt = 0;
// s2里的编号 i2
int i2 = 0;
// i 映射到 s1cnt, s2cnt
unordered_map<int, pair<int,int>> i2cnt;
while (true)
{
++s1cnt;
// 遍历一个s1
for (char c : s1)
{
if (c == s2[i2])
{
++i2;
// 完成一个s2的匹配
if (i2 == ns2)
{
++s2cnt;
// 要重新计数回到s2的编号0
i2 = 0;
}
}
}
// 发现s1的n1都用完了,依然找不到, 直接计算返回
if (s1cnt == n1)
{
return s2cnt / n2;
}
// 找到之前循环的i2,那么就可以循环计算了
if (i2cnt.find(i2) != i2cnt.end())
{
int s1cntPre = i2cnt[i2].first;
int s2cntPre = i2cnt[i2].second;
// 开始估算
// (已经得到 s2cnt 的数量) + (剩下数量可以构建重复的 s2cnt 数量)
int res = s2cntPre + (n1 - s1cntPre)/(s1cnt-s1cntPre) * (s2cnt - s2cntPre);
// cout << s1cntPre <<","<<s2cntPre << " " << (s1cnt-s1cntPre) <<","<< (s2cnt - s2cntPre) <<":"<< res << endl;
// 剩下数量不足s1cntPre的则继续遍历
int nRest = (n1 - s1cntPre) % (s1cnt-s1cntPre);
for (int i = 0; i < nRest; ++i)
{
for (char c : s1)
{
if (c == s2[i2])
{
++i2;
if (i2 == ns2)
{
++res;
i2 = 0;
}
}
}
}
// 最后需要除以 n2 才是真正结果
return res / n2;
}
else
{
i2cnt[i2] = {s1cnt, s2cnt};
}
}
return 0;
}
};
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
- Python教程
- 深入理解 MySQL 中的 HAVING 关键字和聚合函数
- Qt之QChar编码(1)
- MyBatis入门基础篇
- 用Python脚本实现FFmpeg批量转换
- 力扣228. 汇总区间
- Java 通过 filter 过滤器对请求参数进行处理并修改
- Python使用HTTP代理实现网络请求的自动化
- 17.蒙特卡洛强化学习-根据轨迹估计状态值函数(1)
- Java8新特性:函数式(Functional)接口
- FPGA设计时序约束十六、虚拟时钟Virtual Clock
- 喜讯 | 聚铭网络斩获“ISC 2023数字安全创新能力百强”两项殊荣
- Vue学习计划-Vue3--核心语法(九)slot插槽
- P1506 拯救oibh总部
- 数据结构学习 jz43 数字 1 的个数