蓝桥杯省赛无忧 第二章 基础算法 课件23 递归

01 递归的介绍

02 递归如何实现

03 递归和循环的比较

04 例题讲解

斐波那契数列的直接递归实现在n很大时效率极低，因为它会重复计算很多子问题。对于n <= 100000，我们必须使用一个更高效的方法来计算斐波那契数列的第n项。

一种高效的方法是使用动态规划，我们可以用一个数组来存储已经计算过的斐波那契数，这样可以避免重复计算。但是对于n非常大的情况，像100000这样的n，使用数组来存储每一个斐波那契数也是不现实的，因为这会占用大量的内存。

更好的方法是使用两个变量来存储最近计算的两个斐波那契数，并利用这两个数来计算下一个斐波那契数，这种方法被称为迭代方法。
#include <bits/stdc++.h>
using namespace std;
const int MOD = 1e9 + 7;
int main() {
    long long n;
    cin >> n;
    // 使用模运算的性质简化计算
    long long a = 1, b = 1;
    for (int i = 3; i <= n; ++i) {
        long long c = (a + b) % MOD;
        a = b;
        b = c;
    }
    cout << b << endl;
    return 0;
}

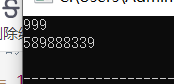
#include<bits/stdc++.h>
using namespace std; 
int n;
int f[1010];
int main()
{
    cin>>n;
    f[1]=1;
    for(int i=2;i<=n;i++)
    {
        if(i&1)
            f[i]=f[i-1];//如果是奇数就和上一个偶数一样
        else
            f[i]=f[i-1]+f[i/2];//如果是偶数就比上一个奇数多了i/2作为结尾的可能性
    }
    cout<<f[n];
    return 0;
}