多传感器融合SLAM数学学习历程

多传感器融合SLAM数学学习历程

>>>流形和流形空间（姿态）

https://blog.csdn.net/professor_Xie/article/details/131911894

欧式空间和流形空间的区别和联系?

基本结构：欧式空间是我们熟悉的传统三维空间，其中的点由三个实数（x、y、z）表示，具有直角坐标系。在欧式空间中，可以进行常规的线性运算和加法操作。而流形空间是一种更一般的概念，它在局部上与欧式空间同胚，但在全局范围内可能不是直角坐标系。

维度：欧式空间的维度是固定的，例如三维欧式空间就有三个坐标轴（x、y、z）。而流形空间的维度可以是任意的，取决于流形的定义。例如，SO(3)流形是三维的，而SO(2)流形是二维的。
————————————————
版权声明：本文为CSDN博主「( ?_?)」的原创文章，遵循CC 4.0 BY-SA版权协议，转载请附上原文出处链接及本声明。
原文链接：https://blog.csdn.net/professor_Xie/article/details/131911894

将姿态定义在流形上比定义在欧式空间上有什么好处？

连续性：姿态定义在流形空间中时，旋转操作的组合和插值都保持了流形的连续性。这意味着在流形空间上进行旋转操作时，不会出现突变或不连续性，从一个姿态平滑地过渡到另一个姿态。

不会出现奇异性：在流形空间上定义姿态可以避免一些奇异性问题。在欧式空间中，例如使用欧拉角时，存在万向锁问题，导致某些方向上的旋转变得不稳定。而在流形空间上，使用四元数或旋转矩阵等表示方式，可以避免这些奇异性问题，从而提高了姿态的稳定性。（欧式空间中姿态表示使用欧拉角）

避免过度参数化：姿态定义在流形空间上通常采用最小的参数化方式，例如四元数、旋转矩阵等。相比之下，在欧式空间中使用欧拉角时，可能会存在多种表示方式表示相同的旋转，导致过度参数化，增加了问题的复杂性。

保持结构特性：在流形空间上定义姿态，比如三维旋转群（SO(3)），可以保持旋转矩阵的正交性和行列式等于1的特性。这保证了旋转操作仍然是合法的旋转。

Example：

>>>李群李代数

视觉slam十四讲
https://zhuanlan.zhihu.com/p/395668394?utm_id=0
李群李代数的定义、相互间关系
李群的指数映射和对数映射
李代数求导、BCH近似、扰动模型
Sophus例程源码解析

>>>卡尔曼滤波

SO(3)流形上的ESKF，相比于四元数形式或欧拉角形式g=更简洁
https://blog.csdn.net/whatiscode/article/details/126242319?spm=1001.2014.3001.5501

SO(3)流形上的ESKF
https://zhuanlan.zhihu.com/p/441182819

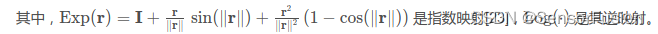
>>>LIO系统

https://blog.csdn.net/whatiscode/article/details/126371351?spm=1001.2014.3001.5501

可参考LI-init标定算法，借鉴了fast-lio2
https://blog.csdn.net/whatiscode/article/details/126252173?spm=1001.2014.3001.5501