【数据结构与算法】排序算法：直接插入排序，希尔排序详解

目录

一、直接插入排序

1、直接插入排序思想

2、直接插入排序算法的性能分析

?编辑

代码实现：

二、希尔排序

1、希尔排序思想

2、希尔排序算法的性能分析

代码实现：?

---

一、直接插入排序

1、直接插入排序思想

直接插入排序是一种简单直观的排序算法，其思想是通过构建已排序部分和未排序部分，将待排序元素按照大小逐个插入到已排序部分的正确位置中，完成排序。

具体步骤如下：

1. 将待排序序列的第一个元素看作已排序部分。
2. 从待排序序列中依次取出元素，从已排序部分的末尾开始，向前比较。
3. 如果当前取出的元素大于已排序部分的某个元素，则将该元素插入到该位置后面，即将该位置以及其后面的元素都向后移动一位。
4. 如果当前取出的元素小于或等于已排序部分的某个元素，则将该元素插入到该位置前面的位置。
5. 重复步骤2-4，直到待排序部分中的所有元素都被插入到已排序部分中

2、直接插入排序算法的性能分析

时空复杂度:

• 时间复杂度：直接插入排序的平均时间复杂度为O(n^2)，最好情况下的时间复杂度为O(n)，最坏情况下的时间复杂度为O(n^2)。
• 空间复杂度：直接插入排序的空间复杂度为O(1)，它是一种原地排序算法，不需要额外的空间。

稳定性：
直接插入排序是稳定的，即相等元素的相对次序在排序前后保持不变。当比较相等元素时，由于只有当前元素小于等于已排序部分的某个元素时才插入，因此相等元素的相对次序不会发生改变。

需要注意的是，尽管直接插入排序在最坏情况下的时间复杂度较高，但对于小规模或基本有序的序列，直接插入排序的性能较为优秀。

代码实现：

void InsertSort(int* a, int n)
{
    int i, j, temp;
    for (i = 0; i < n - 1; i++)
    {
        temp = a[i + 1]; // 将当前待插入的元素暂存到变量temp中
        j = i; // j用于记录已排序部分的最后一个元素的索引
        while (j >= 0)
        {
            if (temp < a[j])
            {
                a[j + 1] = a[j]; // 如果temp比已排序部分的元素小，将该元素后移一位
            }
            else
            {
                break; // 如果temp不小于已排序部分的元素，跳出循环
            }
            j--; // 继续向前比较
        }
        a[j + 1] = temp; // 将暂存的元素插入到正确位置
    }
}

---

二、希尔排序

1、希尔排序思想

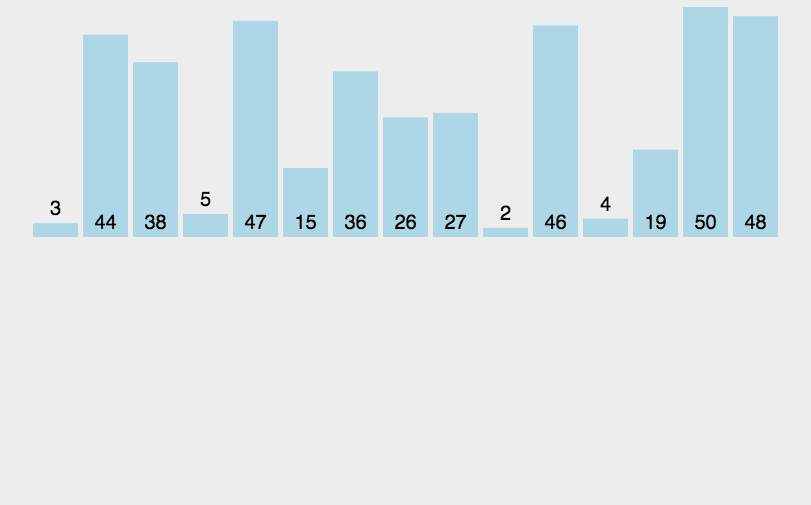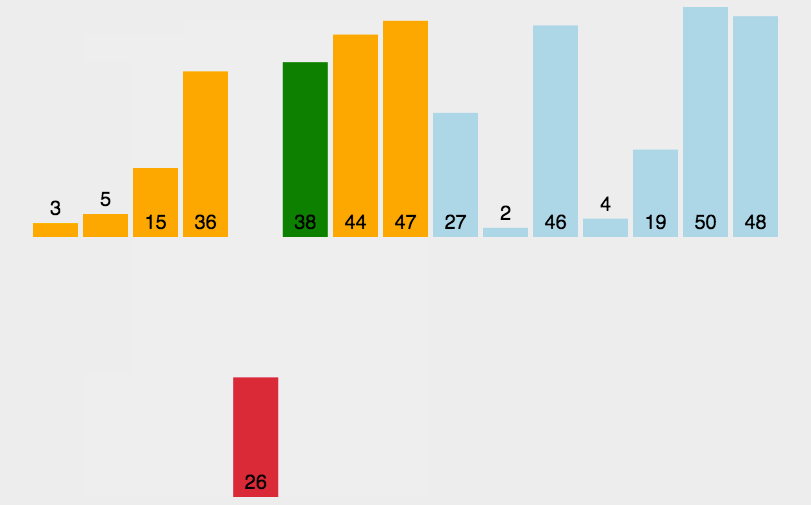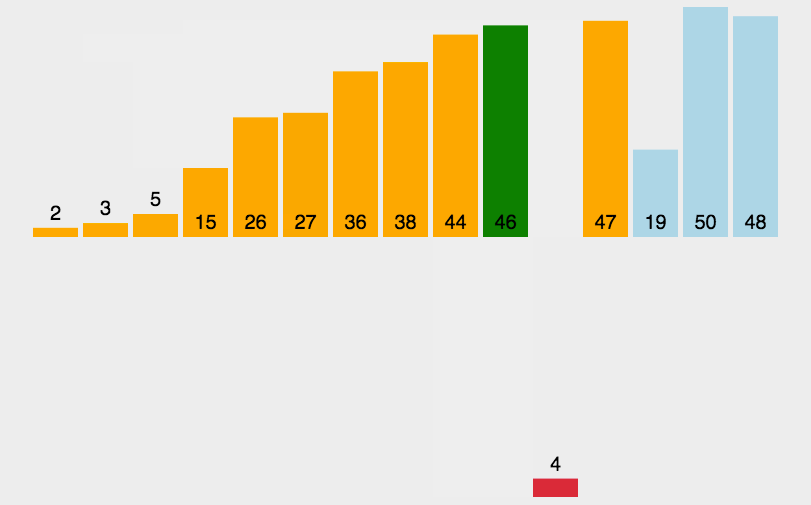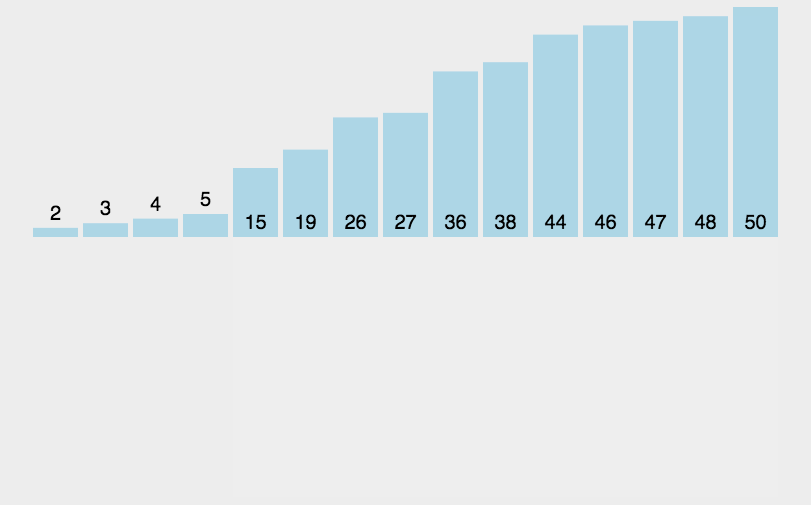
希尔排序是基于插入排序的一种改进算法，也称为缩小增量排序。它通过将待排序序列按照一定间隔分成多个子序列，并对每个子序列进行插入排序的方式来逐步减小间隔，最终使整个序列有序。

具体步骤如下：

1. 选择一个增量序列，通常是除以2逐步缩小得到的序列。
2. 根据增量序列将待排序序列分成多个子序列。
3. 对每个子序列进行插入排序，即将子序列中的元素按照插入排序的方式进行排序。
4. 逐步缩小增量，重复步骤2和步骤3，直到增量为1。
5. 最后进行一次增量为1的插入排序，完成整个序列的排序。

希尔排序的思想是利用了插入排序对基本有序的序列性能较好的特点，通过提前部分排序减少了逆序对的数量，从而提高了排序效率。

2、希尔排序算法的性能分析

时空复杂度:

• 时间复杂度：希尔排序的时间复杂度与增量序列的选择有关，平均时间复杂度为O(nlogn)，最好情况下的时间复杂度为O(nlog^2n)，最坏情况下的时间复杂度为O(n^2)。
• 空间复杂度：希尔排序的空间复杂度为O(1)，它是一种原地排序算法，不需要额外的空间。

稳定性：
希尔排序是不稳定的，因为在每个子序列中进行插入排序时，相等元素的相对次序可能会发生改变。

代码实现：?

void ShellSort(int* a, int n)
{
    int gap = n; // 设置初始的增量gap为序列长度
    int temp, i, j;
    while (gap > 1)
    {
        gap = gap / 2; // 缩小增量
        for (i = 0; i < n - gap; i++)
        {
            temp = a[i + gap]; // 将当前待插入的元素暂存到变量temp中
            j = i;
            while (j >= 0)
            {
                if (temp < a[j])
                {
                    a[j + gap] = a[j]; // 如果temp比已排序部分的元素小，将该元素后移gap位
                    j -= gap; // 向前移动gap位
                }
                else
                {
                    break; // 如果temp不小于已排序部分的元素，跳出循环
                }
            }
            a[j + gap] = temp; // 将暂存的元素插入到正确位置
        }
    }
}