[蓝桥杯知识学习] 树链

DFS序

什么是DFS序

怎么求DFS序

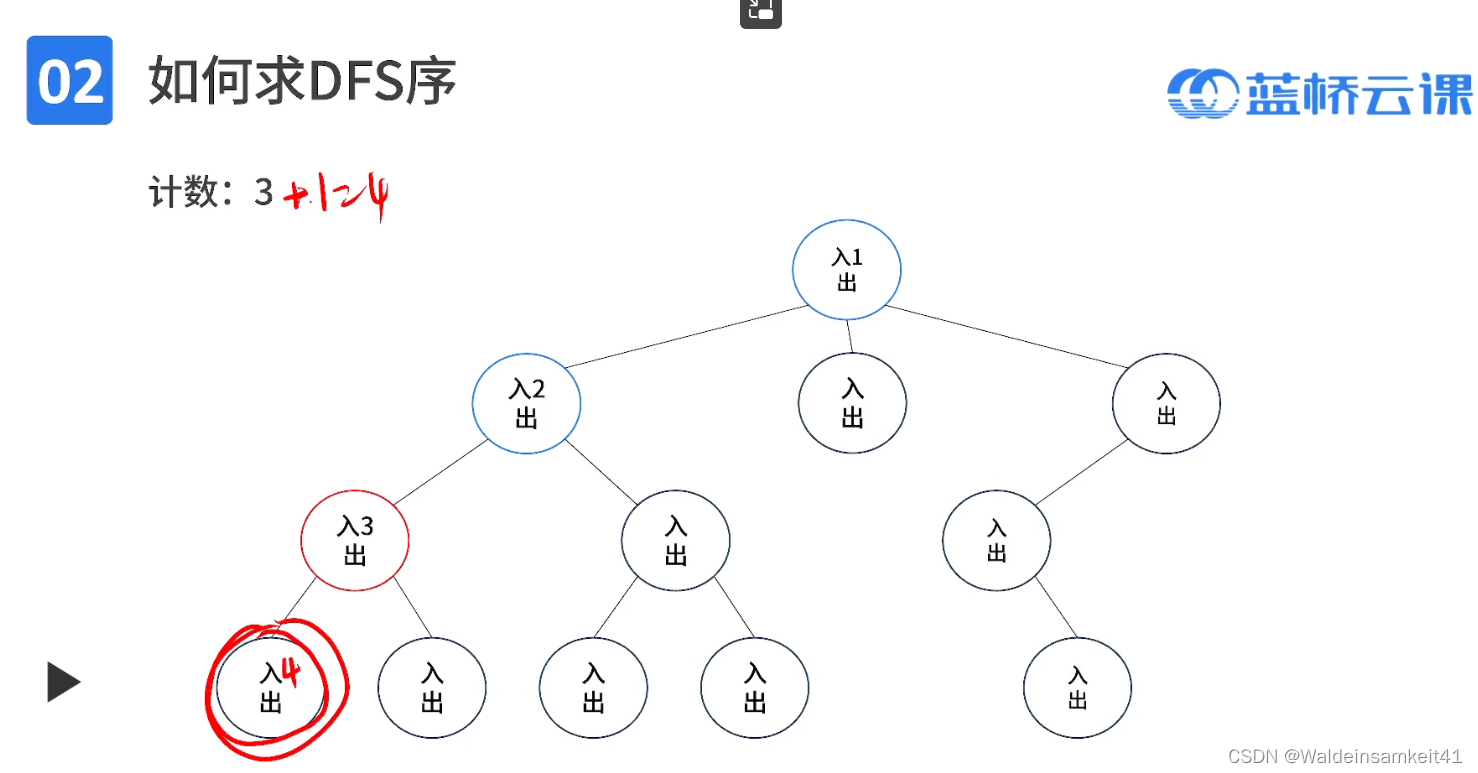
进入操作，将有计数++

出：可以理解为，没有孩子可以去了（不能，向下行动：对应于程序里的入栈），所以回到父结点（向上行动，对应于程序里的出栈）

总体行动：

1. 进入结点，计数++，赋值：入=当前计数

2. 如果可以向下，则重复1操作

3. 如果没有可以向下的了，则，在当前结点：赋值出=当前计数，回到父结点，重复2操作

代码实现

我自己写的，更好懂

//多叉树
int inn[100000];  //dfs入序
int out[100000];   //dfs出序
int weight[100000];  //权重
vector<int> edge[100000];  //用来放结点的子结点
int cnt;  //dfs序计数器

//生成dfs序
void dfs(int t,int f)
{
  inn[t] = ++cnt;
  for(int i = 0 ; i < edge[t].size() ; i++)
  {
    dfs(edge[t][i],t);
  }
  out[t] = cnt;
  return ;
}

其实就是三段论

用一个数组 in 存放该结点的入序，遍历这个结点所有的子结点，用一个数组 out 放出序

DFS序的性质

1. 某些连续的入序对应树中的节点是一条链

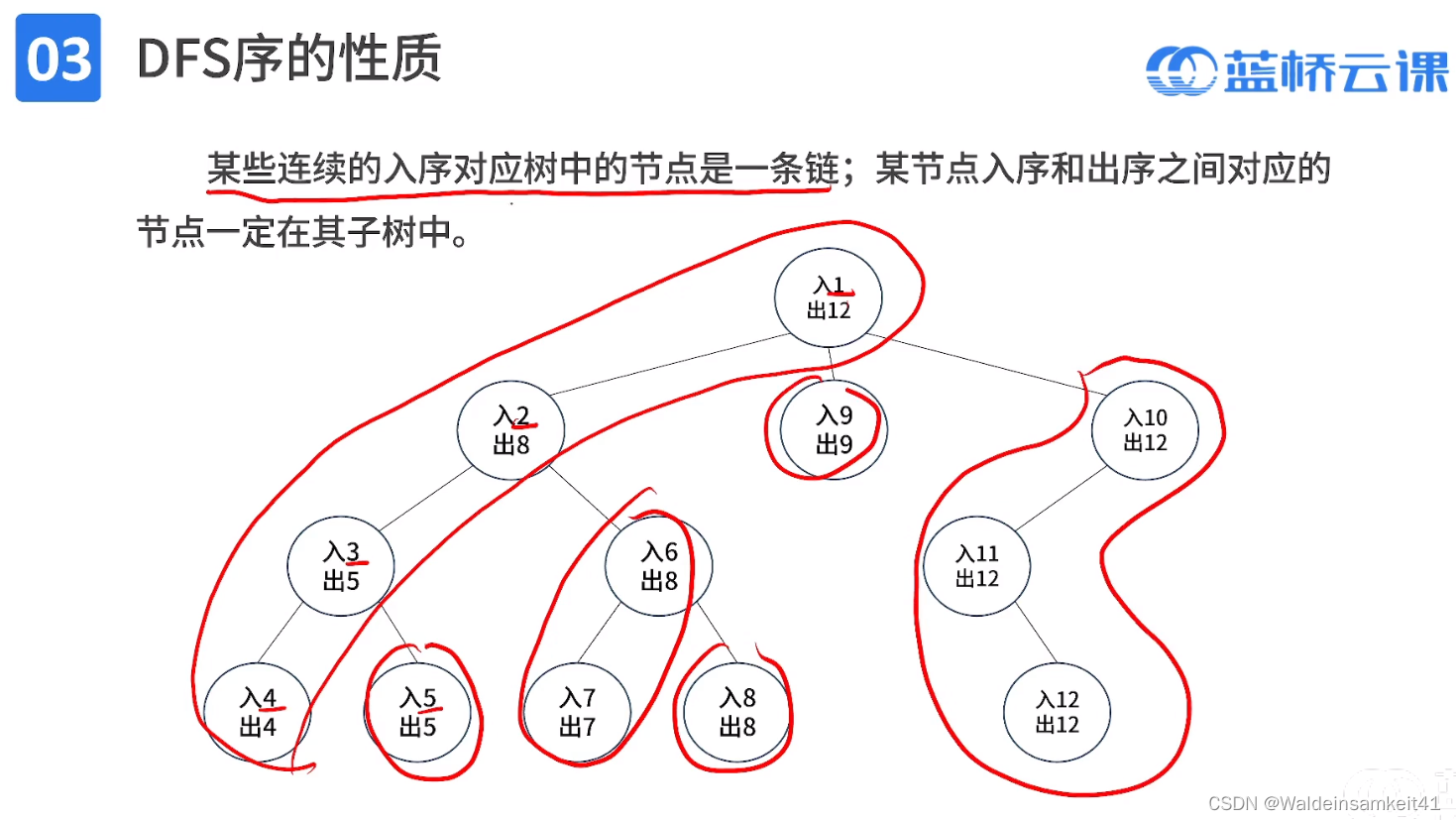
2.某节点入序和出序之间对应的节点一定在其子树中

某结点的子树，其子树上的结点入序数都大于该结点，出序数都小于该结点。（这个好理解，要先进入这个结点，才能向下；向上的话，这个结点在最上方）

出序，一路退出，和最后进入的结点计数值相同

in[t] < t的子树的DFS序?< out[t]

例题

涉及到子树，所以用DFS序

解释，为什么第一个操作用的是 in[x] （某点的DFS序值），因为我们使用DFS序值当作数组下标，来记录点的点权，方便第二个操作的进行。

解释第二个操作：使用DFS序的第二个性质，in[x] 与 out[x] 之间是x子树结点的DFS序。