手撕HashMap
发布时间:2023年12月27日
什么是HashMap(理论+代码)
HashMap存储的键值对Key-Value,Key具有唯一性,采用了链地址法来处理哈希冲突,当往 HashMap 中添加元素时,会计算 key 的 hash 值取余得出元素在数组中的的存放位置。
HashMap数据结构
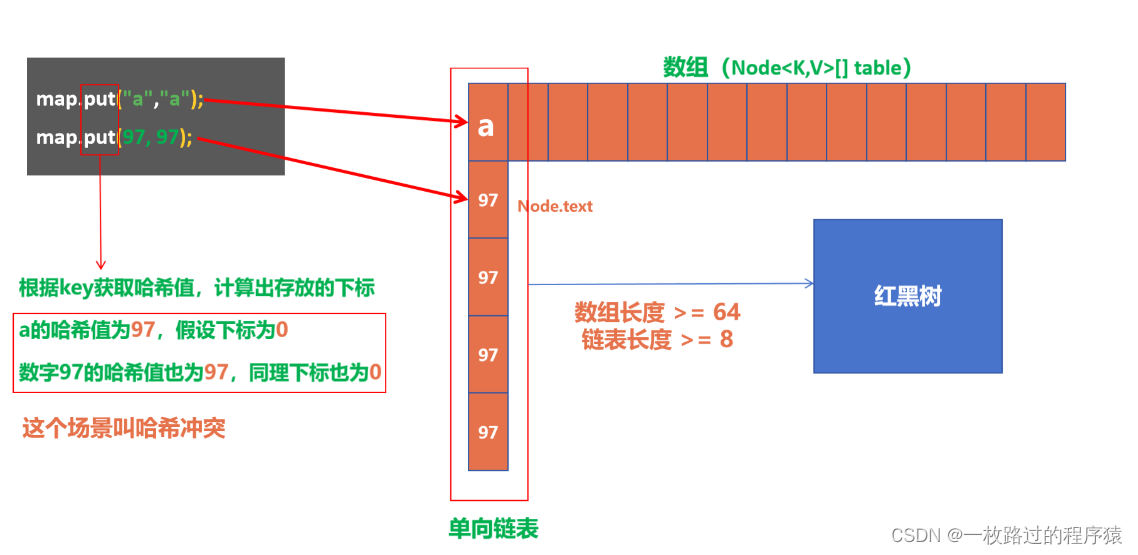
由上图可见,HashMap是由 数组 + 链表 + 红黑树实现,首先我们插入元素的元素是存放至数组,如果插入的位置存在元素,这个时候会存放至元素的下一位,这个就叫链表,如果链表元素数量大于等于8,并且数组长度大于等于64,会把列表转换为红黑树,这就是HashMap处理逻辑
扩容算法
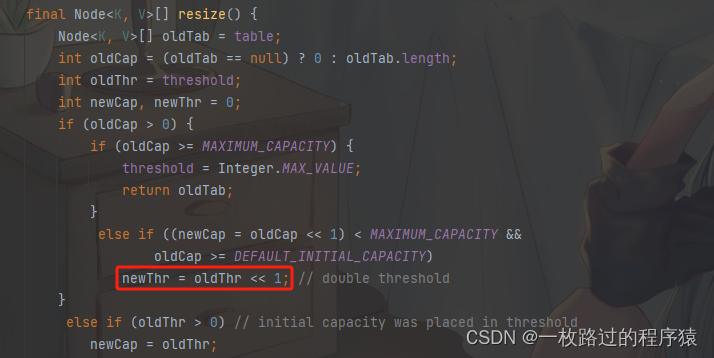
上图可见:resize()方法是HashMap扩容方法
其中扩容的核心代码为newThr = oldThr << 1;,表示新数组长度 = 旧组数长度 * 2
哈希冲突算法
static final int hash(Object key) {
int h;
return (key == null) ? 0 : (h = key.hashCode()) ^ (h >>> 16);
}
核心代码为:(h = key.hashCode()) ^ (h >>> 16),通过位移和异或生成一个相对均匀分布的哈希值尽量减小哈希冲突的可能性
我们可以发现当key为null时,默认返回0,由此可见:HashMap是允许key为null
HashMap代码
了解完以上基础理论之后,我们可以实现一个自己的HashMap,以下代码实现了完整的数据结构,红黑树的转换,扩容等等,具体可以查看代码详细注释
欢迎访问源代码仓库,里面收集了树型结构、List等源码,后续会持续更新源码系列 tryCode
/**
* @Description:
* @Author 一枚路过的程序猿
* @Version 1.0
*/
public class MyHashMap<K extends Comparable<K>,V> {
/** 初始长度 */
final int DEFAULT_CAPACITY = 16;
/** 扩容比例 */
final float DEFAULT_LOAD_FACTOR = 0.75f;
/** 扩容基数 */
int threshold;
/** 初始全局数组 */
Node<K,V>[] tab;
/** 数组长度 */
int size;
/** 单个哈希桶链表长度阈值,进行转换红黑树 */
static final int TREEIFY_THRESHOLD = 8;
/** 数组长度阈值,进行转换红黑树*/
static final int MIN_TREEIFY_CAPACITY = 64;
/**
* 添加方法
* @param k 键
* @param v 值
*/
public void put(K k, V v){
/** 根据 Key 获取哈希值 */
int hashCode = getHashCode(k);
/** 初次执行数组为空 */
if (tab == null) {
/** 调用 (扩容 + 初始化) 方法 */
grow();
}
/**
* 使用 数组长度-1 与运算 哈希值,
*
* 这样设计的好处:与运算是确保下标范围,防止越界;提高查询节点效率,位运算的操作效率是最高的;可以体现出一部分散列分布
*
* 与用算符表示:两个操作数中位都为1,才为1,否则为0
* 例:
* 001010001 -> 81
* 111011001 -> 473
* ——————————————
* 001010001 -> 81
*
*/
int i = (tab.length - 1) & hashCode;
/** 校验具体节点是否为空,不为空表示存在哈希冲突,否则直接插入 */
if (tab[i] != null) {
Node<K, V> node = tab[i];
if (k == node.key || k.equals(node.key)) {
node.value = v;
return;
}else if(node instanceof TreeNode){
((TreeNode<K, V>) node).add(k, v, hashCode, null);
}else{
for(int binCount = 0; ;++binCount){
if (node.next == null) {
node.next = new Node<K, V>(hashCode,k,v,null);
if(binCount >= TREEIFY_THRESHOLD - 1){
/** 转换为红黑树 */
convertRBT(i);
}
break;
}
node = node.next;
}
}
}else { /** 不存在哈希冲突,直接插入 */
tab[i] = new Node<K, V>(hashCode,k,v,null);
}
/** 校验是否达到扩容阈值 */
if (++size >= threshold) {
grow();
}
}
/**
* 转换为红黑树
* 数组长度大于等于64,并且链表长度大于等于7
*
* @param index
*/
private void convertRBT(Integer index) {
/** 如果数组长度小于64,直接进行扩容 */
if(tab == null || tab.length < MIN_TREEIFY_CAPACITY){
grow();
}else { /** 转换红黑树 */
Node<K, V> node = tab[index];
//TODO 转换为红黑树之后不保留之前的链表结构,源代码中是有保留链表结构:
// 1. 维护两种数据结构是为了在不同负载情况下优化性能。在哈希表的生命周期内,可能会经历不同的负载阶段,有些阶段适合链表,有些阶段适合红黑树。动态地在这两者之间切换,可以在不同负载情况下兼顾时间和空间的性能。
// 2. 节点数量小于等于6的时候,会把红黑树转为链表继续存储,具体方法代码: # final void split(HashMap<K,V> map, Node<K,V>[] tab, int index, int bit)
/** 构建红黑树对象 */
TreeNode<K, V> treeNode = new TreeNode<K, V>();
do {
/** 插入红黑树 */
treeNode.add(node.key, node.value, node.hash, node.next);
node = node.next;
}while (node.next != null);
/** 更新数组指向为红黑树 */
tab[index] = treeNode;
}
}
/**
* 扩容加初始化
*/
private void grow() {
Node<K,V>[] oldTab = tab;
/** 如果原数组是null的,进行初始化,否则扩容长度 */
int newSize = (oldTab == null ? 0 : oldTab.length << 1);
if(newSize > 0){
/** 扩容 + 数据迁移 */
Node<K,V>[] newTab = new Node[newSize];
for (int i = 0; i < oldTab.length; i++) {
Node<K, V> node = oldTab[i];
if (node != null) {
newTab[(newTab.length - 1) & node.hash] = node;
}
}
tab = newTab;
threshold = (int) (newSize * DEFAULT_LOAD_FACTOR);
}else {
/** 初始化 */
tab = new Node[DEFAULT_CAPACITY];
threshold = (int) (DEFAULT_CAPACITY * DEFAULT_LOAD_FACTOR);
}
}
/**
* 获取元素
* @param k key
* @return 值
*/
public V get(K k){
/** 校验数组是否为空 */
if (tab == null) {
return null;
}
/** 根据key获取哈希值 */
int hashCode = getHashCode(k);
/** 计算哈希桶下标 */
int i = (tab.length - 1) & hashCode;
/** 校验单个哈希桶是否为空 */
if (tab[i] != null) {
/** 获取哈希桶 */
Node<K, V> node = tab[i];
/** 校验节点是否红黑树 */
if(node instanceof TreeNode){
TreeNode<K, V> treeNode = (TreeNode<K, V>) node;
node = treeNode.getNode(k);
if (node != null) {
return node.value;
}
}else { /** 链表结构 */
do {
/** 链表结构 */
if (node.key == k || node.key.equals(k)) {
return node.value;
}
node = node.next;
}while (node != null);
}
}
return null;
}
/**
* 删除方法
* @param k key
* @return 值
*/
public V remove(K k){
/** 校验数组或者key是否为空 */
if (tab == null || k == null) {
return null;
}
/** 根据key获取哈希值 */
int hashCode = getHashCode(k);
/** 计算哈希桶下标 */
int i = (tab.length - 1) & hashCode;
if(tab[i] != null){
Node<K, V> node = tab[i];
/** 如果是红黑树,调用红黑树删除 */
if(node instanceof TreeNode){
TreeNode<K, V> treeNode = ((TreeNode) node);
treeNode.remove(k);
tab[i] = treeNode;
return node.value;
}else { /** 处理链表情况 */
if(node !=null && node.next == null){
if (node.key == k || node.key.equals(k)) {
tab[i] = null;
return node.value;
}
}
while (node != null && node.next != null) {
/** 链表结构 */
if (node.next.key == k || node.next.key.equals(k)) {
node.next = (node.next.next);
tab[i] = node;
return node.next.value;
}
node = node.next;
}
}
}
throw new IllegalArgumentException("invalid key");
}
/**
* 获取HashCode
* @param k key
* @return 哈希值
*/
private int getHashCode(K k) {
return k == null ? 0 : k.hashCode();
}
/**
* 链表
* @param <K>
* @param <V>
*/
static class Node<K,V>{
/** 哈希值 */
int hash;
/** K */
K key;
/** V */
V value;
/** 下一个 */
Node<K,V> next;
public Node() {
}
public Node(int hash, K key, V value, Node<K, V> next) {
this.hash = hash;
this.key = key;
this.value = value;
this.next = next;
}
}
/**
* 红黑树
* @param <K>
* @param <V>
*/
static class TreeNode<K extends Comparable<K>, V> extends Node<K,V>{
public TreeNode() {
super();
}
TreeNode(int hash, K key, V value, Node<K, V> next) {
super(hash, key, value, next);
}
boolean red;
TreeNode<K, V> parent;
TreeNode<K, V> left;
TreeNode<K, V> right;
TreeNode<K, V> root;
public void add(K k, V v, Integer hash, Node<K,V> next){
TreeNode<K, V> node = new TreeNode<K, V>(hash, k, v, next);
if (root == null) {
root = node;
}else{
node.red = true;
TreeNode<K, V> tempNode = root;
for(;;){
int i = k.compareTo(tempNode.key);
/** 小于的话从左边插入 */
if (i < 0) {
if (tempNode.left == null) {
node.parent = tempNode;
tempNode.left = node;
break;
}
tempNode = tempNode.left;
/** 大于的话从右边插入 */
}else if (i > 0){
if (tempNode.right == null) {
node.parent = tempNode;
tempNode.right = node;
break;
}
tempNode = tempNode.right;
/** 等于更新值 */
}else {
node.value = v;
return;
}
}
balanceInsertion(node);
}
}
private void balanceInsertion(TreeNode<K, V> node) {
if (node != null && node != root && node.parent.red) {
/** 校验当前是否是左子树 */
if(node.parent == node.parent.parent.left){
/**
*
* 校验是否存在叔叔节点,如果存在
* 1.父亲节点和叔叔节点变为黑色
* 2.爷爷节点变为红色
* 3.以爷爷节点进行递归插入(防止爷爷节点之上还有其余节点,导致整棵树不平衡)
*
* 3
* / \
* 1 4
* /
* 0
*
* */
if(node.parent.parent.right != null && node.parent.parent.right.red){
node.parent.red = false;
node.parent.parent.right.red = false;
node.parent.parent.red = true;
balanceInsertion(node.parent.parent);
}else { /** 不存在叔叔节点 */
/**
*
* 校验节点是否在右侧,如果是,首先以父亲节点进行一次左旋操作,变成普通左子树
*
* 3 3
* / /
* 1 2
* \ /
* 2 1
*
* */
if(node == node.parent.right){
/** 左旋 */
rotateLeft(node.parent);
}
/**
*
* 如果是普通左子树
* 1.父亲节点变为黑色
* 2.爷爷节点变为红色
* 3.然后进行右旋
* 4.以爷爷节点进行递归插入(防止爷爷节点之上还有其余节点,导致整棵树不平衡)
*
* 3 1
* / / \
* 1 0 3
* /
* 0
*
* */
/** 变色 */
node.parent.red = false;
node.parent.parent.red = true;
/** 右旋 */
rotateRight(node.parent.parent);
/** 继续向上递归 */
balanceInsertion(node.parent.parent);
}
}else { /** 右子树 */
/**
*
* 校验是否存在叔叔节点,如果存在
* 1.父亲节点和叔叔节点变为黑色
* 2.爷爷节点变为红色
* 3.以爷爷节点进行递归插入(防止爷爷节点之上还有其余节点,导致整棵树不平衡)
*
* 3
* / \
* 1 4
* \
* 0
*
* */
if(node.parent.parent.left != null && node.parent.parent.left.red){
node.parent.red = false;
node.parent.parent.left.red = false;
node.parent.parent.red = true;
balanceInsertion(node.parent.parent);
}else { /** 不存在叔叔节点 */
/**
*
* 校验节点是否在左侧,如果是,以父亲节点进行一次右旋操作,变成普通右子树
*
* 3 3
* \ \
* 1 2
* / \
* 2 1
*
* */
if(node == node.parent.left){
/** 右旋 */
rotateRight(node.parent);
}
/**
*
* 如果是普通右子树
* 1.父亲节点变为黑色
* 2.爷爷节点变为红色
* 3.然后进行左旋
* 4.以爷爷节点进行递归插入(防止爷爷节点之上还有其余节点,导致整棵树不平衡)
*
* 3 1
* \ / \
* 1 0 3
* \
* 0
*
* */
/** 变色 */
node.parent.red = false;
node.parent.parent.red = true;
/** 右旋 */
rotateLeft(node.parent.parent);
/** 继续向上递归 */
balanceInsertion(node.parent.parent);
}
}
}
root.red = false;
}
public void remove(K k){
/** 查找到节点 */
TreeNode<K, V> node = getNode(k);
if (node == null) {
return;
}
/** 第三种情况:删除结点有两个叶子节点,需要使用前驱查找或者后继查找来替换 */
if (node.left != null && node.right != null){
/** 采用前驱查找 */
TreeNode<K, V> n = precursorFind(node);
/** 修改值为待删除的值 */
node.value = n.value;
/**
* 把当前要删除的节点修改为后继查找的节点
*
* 3
* / \
* 2 10 -- 11 比如这个时候要删除 10节点,我们通过(后继查找)查找到了 11节点,
* / \ 只需要将10修改为11,然后删除 11节点即可
* 9 11 -- 删除
*
*/
node = n;
}
/** 找到需要替换的节点 */
TreeNode<K, V> n = node.left != null ? node.left : node.right;
/** 第二种情况:删除节点有一个叶子节点的,那么用叶子节点来代替 */
if(n != null){
/** 直接关联,跳过待删除节点 */
n.parent = node.parent;
/** 如果删除节点的父节点为空,表示删除之后只会存在一个节点,直接指向root */
if(node.parent == null){
root = n;
/** 如果删除节点在父节点的左边,把替换节点关联到父节点的左边 -> 双向绑定 */
}else if(node == node.parent.left){
node.parent.left = n;
/** 如果删除节点在父节点的右边,把替换节点关联到父节点的右边 -> 双向绑定 */
}else {
node.parent.right = n;
}
/** help GC */
node.right = node.left = node.parent = null;
/** 调整红黑树平衡,只有删除黑色节点时,需要调整平衡,因为其余的都是修改,不会发生树调整 */
if(!node.red){
fixTree(n);
}
/** 第一种情况:删除叶子节点,直接删除 */
}else {
/** 此处需要先进行调整平衡,然后再删除 */
if(!node.red){
fixTree(node);
}
/** 如果只有一个叶子节点,并且没有父类,删除之后,整棵树为空,置空root节点 */
if (node.parent == null) {
root = null;
/** 如果删除节点在父节点的左边,把替换节点关联到父节点的左边 -> 双向绑定 */
}else if (node == node.parent.left) {
node.parent.left = null;
/** 如果删除节点在父节点的右边,把替换节点关联到父节点的右边 -> 双向绑定 */
}else {
node.parent.right = null;
}
/** help GC */
node.parent = null;
}
}
/**
* 调整树平衡
* @param node
*/
private void fixTree(TreeNode<K, V> node) {
while (node != root && !node.red){
/** 校验节点是左节点还是右节点 */
if(node == node.parent.left){
/** 获取兄弟节点 */
TreeNode<K, V> r = node.parent.right;
// 校验是不是真的兄弟节点
if(r.red){
r.red = false;
node.parent.red = true;
rotateLeft(node.parent);
r = node.parent.right;
}
/** 当兄弟节点一个子节点都没有,或者两个子节点都是黑色 */
if (r.left == null && r.right == null || ((r.left != null && !r.left.red) && (r.right != null && !r.right.red))) {
r.red = true;
node = node.parent;
}else { /** 至少存在一个子节点 */
/**
* 如果兄弟节点的子节点是左子节点,需要变色 + 右旋
* */
if(r.right == null){ /** 如果兄弟节点的右子节点为空,左子节点肯定不为空,因为兄弟节点没有子节点的时候,只会进入上的if */
r.red = true;
r.left.red = false;
rotateRight(r);
/** 右旋之后,兄弟节点发生变化,需要重新指定 */
r = node.parent.right;
}
/** 然后根据父节点进行左旋 + 变色 */
r.red = node.parent.red;
node.parent.red = r.right.red = false;
rotateLeft(node.parent);
node = root; /** 退出循环 */
}
}else {
/** 获取兄弟节点 */
TreeNode<K, V> r = node.parent.left;
// 校验是不是真的兄弟节点
if(r.red){
r.red = false;
node.parent.red = true;
rotateRight(node.parent);
r = node.parent.left;
}
/** 当兄弟节点一个子节点都没有,或者两个子节点都是黑色 */
if (r.left == null && r.right == null || ((r.left != null && !r.left.red) && (r.right != null && !r.right.red))) {
r.red = true;
node = node.parent;
}else { /** 至少存在一个子节点 */
/**
* 如果兄弟节点的子节点是左子节点,需要变色 + 右旋
* */
if(r.left == null){ /** 如果兄弟节点的右子节点为空,左子节点肯定不为空,因为兄弟节点没有子节点的时候,只会进入上的if */
r.red = true;
r.right.red = false;
rotateLeft(r);
/** 右旋之后,兄弟节点发生变化,需要重新指定 */
r = node.parent.left;
}
/** 然后根据父节点进行左旋 + 变色 */
r.red = node.parent.red;
node.parent.red = r.left.red = false;
rotateRight(node.parent);
node = root; /** 退出循环 */
}
}
}
node.red = false;
}
public TreeNode<K, V> getNode(K k){
TreeNode<K, V> node = root;
while (node != null && k != null){
int i = k.compareTo(node.key);
if(i < 0){
node = node.left;
}else if(i > 0){
node = node.right;
}else {
return node;
}
}
return null;
}
/**
*
* 左旋:
* <p>
* 3 6
* / \ / \
* 2 6 3 7
* / \ / \
* 5 7 2 5
*/
private void rotateLeft(TreeNode<K, V> node) {
/** 获取右子节点 -> 6 */
TreeNode<K, V> r = node.right;
/** node右子节点设置为 r节点的左子节点 -> ( 3的右子节点设置为5 )*/
node.right = r.left;
/** 校验 r的左子节点 是否为空 */
if (r.left != null) {
/** 设置 r的左子节点父类为node -> ( 5的父类设置为3 ) */
r.left.parent = node;
}
/** 将6的父类设置为3的父类 */
r.parent = node.parent;
/** 校验node节点是否存在父类 */
if(node.parent == null){
/** 根节点直接设置为 r -> ( 根节点直接设置为6 ) */
root = r;
}else if (node.parent.left == node) { /** 校验 node 节点是存在父类的哪边 -> 左 */
node.parent.left = r;
}else { /** 右 */
node.parent.right = r;
}
/** 交换位置 -> (6和3交换位置) */
node.parent = r;
r.left = node;
}
/**
* 右旋:
* <p>
* 6 3
* / \ / \
* 3 7 2 6
* / \ / \
* 2 5 5 7
*
*/
private void rotateRight(TreeNode<K, V> node) {
/** 获取左子节点 -> (3) */
TreeNode<K, V> l = node.left;
/** 更新node左节点为 l的右节点 -> ( 6的左子节点更新为5 ) */
node.left = l.right;
/** 校验 l的右节点 是否为空,不为空的时候进行双向关联 -> ( 5的父类更新为6 )*/
if (l.right != null) {
l.right.parent = node;
}
/** 将3的父类设置为6的父类 */
l.parent = node.parent;
if (node.parent == null) {
/** 根节点直接设置为 r -> ( 根节点直接设置为3 ) */
root = l;
}else if (node.parent.left == node) { /** 校验 node 节点是存在父类的哪边 -> 左 */
node.parent.left = l;
}else { /** 右 */
node.parent.right = l;
}
/** 交换位置 -> (6和3交换位置) */
node.parent = l;
l.right = node;
}
/**
* 前驱节点查询
* 树右边最大的节点
* @param node
* @return
*/
private TreeNode<K, V> precursorFind(TreeNode<K, V> node){
node = node.left;
if (node == null) {
return null;
}
while (node.right != null) {
node = node.right;
}
return node;
}
/**
* 后继节点查询
* 树左边最小的节点
* @param node
* @return
*/
private TreeNode<K, V> subsequentFind(TreeNode<K, V> node){
node = node.right;
if (node == null) {
return null;
}
while (node.left != null) {
node = node.left;
}
return node;
}
}
}
测试代码
public static void main(String[] args) {
// 创建HashMap
MyHashMap<String, String> hashMap = new MyHashMap<String, String>();
// 添加哈希不冲突的key,不少于70个
for (int i = 0; i < 70; i++) {
String key = "Key" + i;
String value = "Value" + i;
hashMap.put(key, value);
}
// 添加哈希冲突的key,不少于10个,但哈希值相同
String collidingKeyPrefix = "CollisionKey";
String collidingValue = "CollisionValue";
for (int i = 0; i < 10; i++) {
String collidingKey = collidingKeyPrefix + i;
// 使用相同的哈希值
int hash = collidingKeyPrefix.hashCode();
// 强制将哈希值设为相同的值
setHash(collidingKey, hash);
hashMap.put(collidingKey, collidingValue+i);
}
String removeKey = "CollisionKey1";
int hash = collidingKeyPrefix.hashCode();
// 强制将哈希值设为相同的值
setHash(removeKey, hash);
//测试红黑树删除情况
hashMap.remove(removeKey);
//测试链表删除情况
hashMap.remove("Key40");
}
// 强制设置对象的哈希值
private static void setHash(Object key, int hash) {
try {
java.lang.reflect.Field field = String.class.getDeclaredField("hash");
field.setAccessible(true);
field.set(key, hash);
} catch (Exception e) {
e.printStackTrace();
}
}
文章来源:https://blog.csdn.net/haodong0313/article/details/135205559
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
最新文章
- Python教程
- 深入理解 MySQL 中的 HAVING 关键字和聚合函数
- Qt之QChar编码(1)
- MyBatis入门基础篇
- 用Python脚本实现FFmpeg批量转换
- Vue3 魔法:轻松删除响应式对象的属性
- C#上位机与欧姆龙PLC的通信07----使用第3方通讯库读写数据
- js如何实现滚动到底部一键回到顶部。
- Redis高可用实验:主从复制+哨兵+集群
- gitcode邀请协作人员
- 中国肺癌情形
- (每日持续更新)信息系统项目管理(第四版)(高级项目管理)考试重点整理第6章 项目管理理论(三)
- Sui 生态排名第一的头部流动性协议 NAVI Protocol 活动进行中
- Halcon模板图像gen_contour_region_xld/find_shape_model
- python基础学习-01