1-23 每日总结

今天学了队列、二叉树的序列遍历，dfs(深搜)，AC的几道题目。

队列;一种先进先出的线性表，它与栈不同的是，栈是允许在一端插入或者删除的线性表，而队列是一端插入另一端删除的线性表；

队列的一些基本操作：

#include "iostream"

using namespace std;

#define maxsize 10
typedef struct {		
	int data[maxsize];		//用静态数组存放队列元素
	int front, rear;		//队头指针和队尾指针
}sqQueue;
 
void initQueue(sqQueue& Q) {
	Q.front = Q.rear = 0;	//初始化队头队尾指针指向0
}
 
bool QueueEmpty(sqQueue& Q) {	//判断队列是否为空
	if (Q.rear == Q.front)		//队空条件
		return true;
	else return false;
}
 
bool EnQueue(sqQueue& Q, int x) {		//入队
	if ((Q.rear + 1) % maxsize==Q.front)//队列已满(队尾指针的下一个位置是队头,代价：牺牲一个存储单元)因为再存入一个队头队尾就指在一起了，和空队列会产生歧义
		return false;
	Q.data[Q.rear] = x;			//将x插入队尾
	Q.rear =(Q.rear + 1) % maxsize;				//队尾指针加1取模
	return true;
}
 
bool DeQueue(sqQueue& Q, int &x) {	//出队
	if (Q.front == Q.rear)			//判断栈空
		return false;
	x = Q.data[Q.front];
	Q.front = (Q.front + 1) % maxsize;
	return true;
}
 
bool Gethead(sqQueue& Q, int& x) {	//查找队头元素
	if (Q.front == Q.rear)			
		return false;
	x = Q.data[Q.front];
	return true;
}
int main() {		//只允许在一头进行插入，另一端进行删除(特点：先进先出)
	int n,x;
	sqQueue Q;	//声明一个队列
	initQueue(Q);
	QueueEmpty(Q);
	EnQueue(Q, 3);
	DeQueue(Q, n);
	Gethead(Q, x);
	//队列元素个数：（rear+Maxsize-front)%Maxsize
 
}

二叉树的三种序列遍历：先序、中序、后序；

先序就是先根结点再左再又，中序是左根右，后序是左右根；具体实现如下代码;

 //二叉树的三种遍历方式
node{
     int data;
     node* left;
     node* right;
}tree,a,c;
void solve1(node * t) {//  先序
    if (t != NULL) {
        cout << t->data;
        solve1(t->left);
        solve1(t->right);
    }
}
void solve2(node* t) { // 中序
    if (t != NULL) {
        solve2(t->left);
        cout << t->data;
        solve2(t->right);
    }
}
void solve3(node* t) {  // 后序
    if (t != NULL) {
        solve3(t->left);
        solve3(t->right);
        cout << t->data;
    }
}
int main() {
    tree.data = 1;
    a.data = 2;
    c.data = 3;
    tree.left = &a;
    tree.right = &c;
    a.left = a.right = NULL;
    c.left = c.right = NULL;
    solve1(&tree);
    return 0;
} 

dfs（深度优先搜所）：?一条路走到底，不撞南墙不回头。就是沿着一条路一直走，直到尽头就退回一个节点走另外一条路，一直递归重复这个过程直到所有的路都走完。

大概的一个模版是这样的：

int check(参数)
{
    if(满足条件)
        return 1;
    return 0;
}
 
void dfs(int step)
{
        判断边界
        {
            相应操作
        }
        尝试每一种可能
        {
               满足check条件
               标记
               继续下一步dfs(step+1)
               恢复初始状态（回溯的时候要用到）
        }
}   

题目链接：https://www.luogu.com.cn/problem/P1443

题解：首先你要知道马是怎么走到，然后将数组全部赋值为-1,使用结构体队列模型，遍历马的八种走法，然后判断要是这个点马可以走到就把这个点放入队列里面。

AC代码：

#include <iostream>
#include <string>
#include <cmath>
#include <iomanip> 
#include <algorithm>
#include <stack>


using namespace std;

using ll = long long;
#define up(h,n) for(int i=h;i<=n;i++)
#define down(h,n) for(int i=h;i>=n;i--)
#define wh(x) while(x--)
#define node struct node
#define ios ios::sync_with_stdio(false)
constexpr int N = 2000005;
constexpr int mod = 1e9 + 7;
typedef int SElemType;

node{
	int x;
	int y;
	int num;//步数
}que[160005]; //创建队列

const int next1[8][2] =  { {2, 1},  {1, 2}, {-2, -1}, {-1, -2}, {2, -1}, {-1, 2}, {-2, 1}, {1, -2} };
int a[405][405];
int main()
{
	int tx, ty;
	int n, m, x1, y1;
	int head = 1, tail = 1;
	cin >> n >> m >> x1 >> y1;
	up(1, n) {//初始化数组为-1
		for (int j = 1; j <= m; j++)
			a[i][j] = -1;
	}
	que[tail].x = x1;
	que[tail].y = y1;
	que[tail].num = a[x1][y1] = 0;//插入队列数据，设置起点坐标，起点坐标标记为0
	tail++;
	while (head < tail) {
		up(0, 7) {// 遍历马的八种情况
			 tx = que[head].x + next1[i][0];
			 ty = que[head].y + next1[i][1];//马下一个坐标
			if (tx<1 || tx>n || ty<1 || ty>m) continue;//判断是否越界
			if (a[tx][ty] == -1) {
				que[tail].x = tx;
				que[tail].y = ty;
				que[tail].num = a[tx][ty] = que[head].num + 1;//插入队列数据
				tail++;
			}
		}
		head++;
	}
	up(1, n) {
		for (int j = 1; j <= m; j++) {
			 cout << left << setw(5) << a[i][j];
		}
		cout << '\n';
	}
	return 0;
}

题目链接：https://www.luogu.com.cn/problem/P2392

题解：用dfs深搜把每一课科目的习题所花的时间分给左脑和右脑都试一下，然后找出最小值。

AC代码：

#include <iostream>
#include <string>
#include <cmath>
#include <iomanip> 
#include <algorithm>
#include <stack>


using namespace std;

using ll = long long;
#define up(h,n) for(int i=h;i<=n;i++)
#define down(h,n) for(int i=h;i>=n;i--)
#define wh(x) while(x--)
#define node struct node
#define ios ios::sync_with_stdio(false)
constexpr int N = 18;
constexpr int mod = 1e9 + 7;
typedef int SElemType;

int a[4], s[4][65];
int sum = 0, left1 = 0, right1 = 0,min1=0;
void dfs(int i, int j) 
{
	if (j >= a[i]) {
		min1 = min(min1, max(left1, right1));//这一科已经计算完，寻找最小值两边大佬使用的最大
		return;                                 //值去和最小值比较，找出最小值

	}
	left1 += s[i][j];
	dfs(i, j + 1);
	left1 -= s[i][j];
	right1 += s[i][j];
	dfs(i, j + 1);
	right1 -= s[i][j];// 这一部分主要是遍历科目的题集分给左脑和右脑都试一下；
	return;
}
int main()
{
	
	up(0, 3) {
		cin >> a[i];
	}
	up(0, 3) {
		for (int j = 0; j < a[i]; j++) {
			cin >> s[i][j];
		}
	}
	up(0, 3) {
		left1 = 0, right1 = 0;
		min1 = 99999;//每科都得从新找最小，所以每次得从新赋值
		dfs(i, 0);
		sum += min1;
	}
	cout << sum;
	return 0;

}

题目链接：https://www.luogu.com.cn/problem/P2404

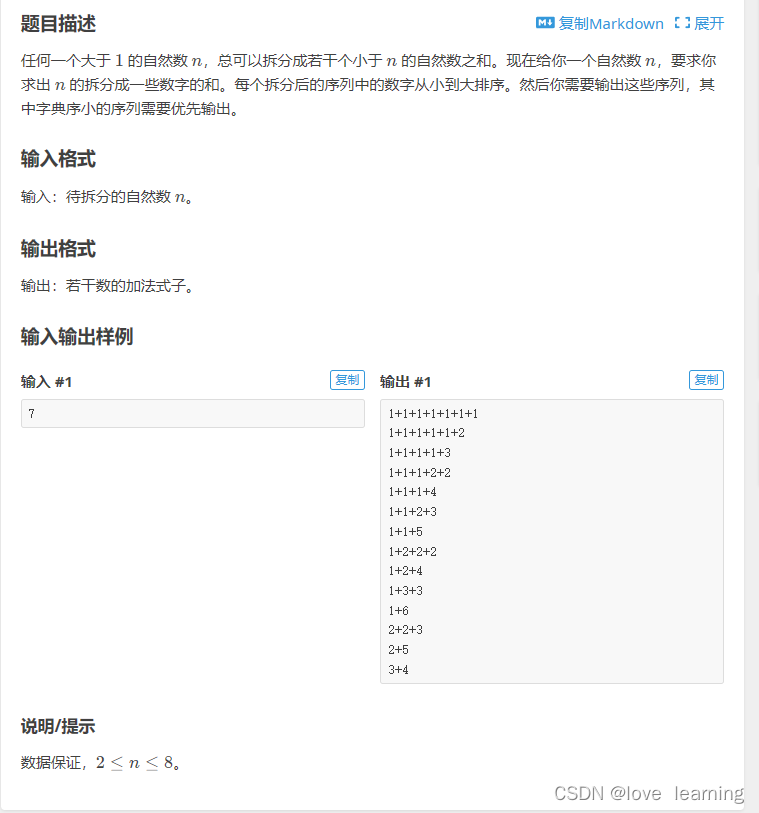
题解：这个题还是比较简单，首先从1开始慢慢往后面深搜，每一次都加上，要是等于n就输出即可

AC代码：

#include <iostream>
#include <string>
#include <cmath>
#include <iomanip> 
#include <algorithm>
#include <stack>


using namespace std;

using ll = long long;
#define up(h,n) for(int i=h;i<=n;i++)
#define down(h,n) for(int i=h;i>=n;i--)
#define wh(x) while(x--)
#define node struct node
#define ios ios::sync_with_stdio(false)
constexpr int N = 18;
constexpr int mod = 1e9 + 7;
typedef int SElemType;

//洛谷 p2404 自然数的拆分问题
int a[9], n;
void dfs(int s, int m, int k) { //s为多少个数 m为开始的数 k为和

	if (k == n) { // 判断如果相等就输出
		up(1, s - 2) {
			cout << a[i] << '+';
		}
		cout << a[s - 1] << '\n';
		return;
	 }
	if (k > n) return; 
	up(m, n - 1) {
		a[s] = i;
		dfs(s + 1, i, k + i);  // 继续往下搜
		a[s] = 0; //回溯
	}
	return;

}
int main()
{
	cin >> n;
	dfs(1, 1, 0);
}

题目链接：https://www.luogu.com.cn/problem/P2036

题解：这一题的话，只需对选取食材和不选取食材两种情况进行dfs然后每次找最小值即可；

AC代码：

#include <iostream>
#include <string>
#include <cmath>
#include <iomanip> 
#include <algorithm>
#include <stack>


using namespace std;

using ll = long long;
#define up(h,n) for(int i=h;i<=n;i++)
#define down(h,n) for(int i=h;i>=n;i--)
#define wh(x) while(x--)
#define node struct node
#define ios ios::sync_with_stdio(false)
constexpr int N = 18;
constexpr int mod = 1e9 + 7;
typedef int SElemType;

int n,min1=99999;
int a[N][N];
void dfs(int i, int x, int y) {
	if (i > n) {
		if (y == 0) return ;
		min1 = min(min1, abs(x - y));
		return;
	}
	dfs(i + 1, x, y);//不选取食材
	dfs(i + 1, x * a[i][0], y+a[i][1]);//选取食材
}
int main() {

	cin >> n;
	up(1, n) {
		cin >> a[i][0] >> a[i][1];
	}
	dfs(1, 1, 0);
	cout << min1;
	return 0;

}