最小二乘法在线性回归中的用法
最小二乘法在线性回归中的用法
最小二乘法是1809年高斯在《天体运动论》中公开发表的一种计算方法。最小二乘法其实是一种“最佳猜测”的方法。想象一下,你有一些数据点,比如你朋友的身高和体重。你想找到一个简单的规则来描述这两者之间的关系。最小二乘法就是帮你找到一条直线,这条直线能够尽可能地接近所有的数据点。这样的直线不会完全通过所有的点(除非所有的点完全在一条直线上)。
可以看到最小二乘法在线性回归中和梯度下降起到的作用是非常类似的,都是去找到一条最优的直线来拟合数据。但差别在于梯度下降是通过一次次计算尝试而求出的结果,梯度下降的方法更通用。最小二乘法则是一组计算公式,直接将数据代入公式就可以获得结果。举个例子,有一个三角形,如果用梯度下降去求三角形的面积就是,随机写一个面积,去和三角形比较,然后如果小了就扩大,如果大了就缩小,慢慢去往三角形的面积去靠。而最小二乘法则是一上来就告诉你底*高/2就是三角形的面积,直接代入就行。
我们在之前的损失函数中已经推导过损失函数的由来:
J
(
θ
)
=
1
2
∑
i
=
1
n
(
h
θ
(
x
i
)
?
y
)
2
J(\theta) = \frac{1}{2} \sum_{i=1}^{n} (h_\theta(x_i) - y)^{2}
J(θ)=21?i=1∑n?(hθ?(xi?)?y)2
将平方展开:
J
(
θ
)
=
1
2
∑
i
=
1
n
(
h
θ
(
x
i
)
?
y
)
(
h
θ
(
x
i
)
?
y
)
J(\theta) = \frac{1}{2} \sum_{i=1}^{n} (h_\theta(x_i) - y)(h_\theta(x_i) - y)
J(θ)=21?i=1∑n?(hθ?(xi?)?y)(hθ?(xi?)?y)
我们理解一下上面的式子:即
h
θ
(
x
i
)
h_\theta(x_i)
hθ?(xi?)【即计算出来的结果】-
y
y
y【即实际结果】和自己相乘再把每个结果都加起来【求和】。
在矩阵中就可以表示为一行
X
θ
?
y
X\theta-y
Xθ?y和自己相乘,只有当一个列向量(竖矩阵)与其自身的转置(行向量)进行点乘时,结果才是一个标量。所以这里就需要把
(
X
θ
?
y
)
?
(X\theta - y)^\top
(Xθ?y)?放在前面进行计算:
J
(
θ
)
=
1
2
(
X
θ
?
y
)
?
(
X
θ
?
y
)
J(\theta) = \frac{1}{2} (X\theta - y)^\top (X\theta - y)
J(θ)=21?(Xθ?y)?(Xθ?y)
如下图,使用转置后(右图)的矩阵去和原矩阵点乘,就实现了每一个结果的累加(求和)。
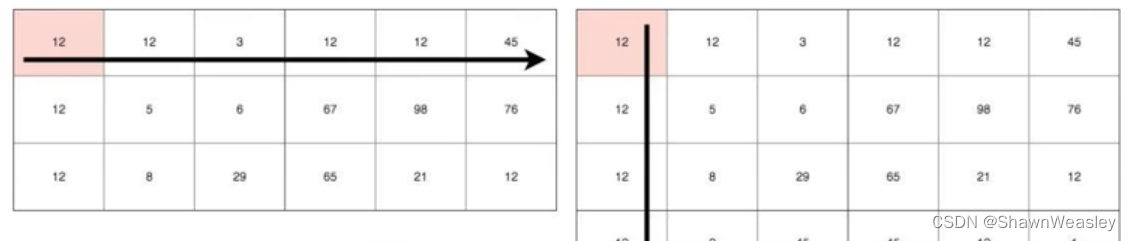
这里的意义就是,比如为下面的式子求解
x
1
x_1
x1?、
x
2
x_2
x2?
{
x
1
+
x
2
=
14
2
x
1
?
x
2
=
10
\begin{cases} x_1 + x_2 = 14 \\ 2x_1 - x_2 = 10 \end{cases}
{x1?+x2?=142x1??x2?=10?
使用代码实现就是:
X = np.array([[1,1],[2,-1]])
y = np.array([14,10])
#执行最小二乘法公式
w = np.linalg.inv(X.T.dot(X)).dot(X.T).dot(y)
print(w)
最小二乘法非常适用于多元函数求解,比如多元一次不等式,如下:
{
x
1
+
x
2
+
2
x
3
=
14
2
x
1
?
x
2
?
x
3
=
10
4
x
1
+
2
x
2
?
7
x
3
=
22
\begin{cases} x_1 + x_2 + 2x_3= 14 \\ 2x_1 - x_2 - x_3= 10\\ 4x_1 + 2x_2 - 7x_3= 22 \end{cases}
?
?
??x1?+x2?+2x3?=142x1??x2??x3?=104x1?+2x2??7x3?=22?
在线性回归中,最小二乘法适用于寻找最适合数据集的直线或平面时,提供一种计算模型参数的解析解。
使用sklearn来实现的话,代码如下:
X = np.array([[1,1],[2,-1]])
y = np.array([14,10])
#执行最小二乘法公式
model = LinearRegression(fit_intercept=False)
model.fit(X, y)
print(model.coef_)
添加截距项的最小二乘法
当自变量为零时,因变量也为零的情况下,使用上述的方法即可。但当一组数据不适用于X=0时y也=0的情况下,我们就需要为 y = θ 1 x 1 + θ 2 x 2 + … + θ n x n y = \theta_1 x_1 + \theta_2 x_2 + \ldots + \theta_n x_n y=θ1?x1?+θ2?x2?+…+θn?xn?添加一个截距项 θ 0 \theta_0 θ0?,这意味着我们的模型需要一个截距项来捕捉 y y y轴上的偏移,以便更准确地描述数据。模型将变为:
y = θ 0 + θ 1 x 1 + θ 2 x 2 + … + θ n x n y = \theta_0 + \theta_1 x_1 + \theta_2 x_2 + \ldots + \theta_n x_n y=θ0?+θ1?x1?+θ2?x2?+…+θn?xn?
其中,
θ
0
\theta_0
θ0?是截距项,它代表了当所有
x
i
x_i
xi?都为 0 时
y
y
y的值。
添加截距项是为了更好的预测不在数据集最大区间内的数据。
这里用公式表示的话就是:会将
{
x
1
+
x
2
=
14
2
x
1
?
x
2
=
10
\begin{cases} x_1 + x_2 = 14 \\ 2x_1 - x_2 = 10 \end{cases}
{x1?+x2?=142x1??x2?=10?转成
{
x
1
+
x
2
+
θ
0
=
14
2
x
1
?
x
2
+
θ
0
=
10
\begin{cases} x_1 + x_2+ \theta_0= 14 \\ 2x_1 - x_2+ \theta_0= 10 \end{cases}
{x1?+x2?+θ0?=142x1??x2?+θ0?=10?这样
x
1
x_1
x1?和
x
2
x_2
x2?的求解值就会发生改变。换句话说,在
{
x
1
+
x
2
+
θ
0
=
14
2
x
1
?
x
2
+
θ
0
=
10
\begin{cases} x_1 + x_2+ \theta_0= 14 \\ 2x_1 - x_2+ \theta_0= 10 \end{cases}
{x1?+x2?+θ0?=142x1??x2?+θ0?=10?这组式子里只要式子1中的
y
y
y和式子2中的
y
y
y的差距保持为4(即14-10),那
x
1
x_1
x1?和
x
2
x_2
x2?的求解就不会变化,因为
y
1
y_1
y1?和
y
2
y_2
y2?是同步变化的,同步变化的结果会被
θ
0
\theta_0
θ0?截距项纠正。
可以尝试一下更改代码中的
y
1
y_1
y1?和
y
2
y_2
y2?同步变化,最终的model.coef_结果不变:
X = np.array([[1,1],[2,-1]])
y = np.array([14,10])
#执行最小二乘法公式
model = LinearRegression(fit_intercept=True)
model.fit(X, y)
print(model.coef_)
实际上代码只更改了fit_intercept的设置来控制是否使用截距项。
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
- Python教程
- 深入理解 MySQL 中的 HAVING 关键字和聚合函数
- Qt之QChar编码(1)
- MyBatis入门基础篇
- 用Python脚本实现FFmpeg批量转换
- vue使用elementui 的 table且自定义某列表头时,添加的点击事件和自带的筛选功能有类似冒泡行为
- 水利水库大坝安全监测参数详解
- uni-app的学习【第三节】
- 使用netty做硬件测试代码的一般步骤
- UE5 C++中 Actor内填加编辑器内模型
- Tomcat Notes: Web Security
- 腾讯云域名解析到另一个域名
- RT-Thread:STM32实时时钟 RTC开启及应用
- 跟随山海鲸开发者,深入了解智慧城市解决方案的核心技术
- 13.8.1异步、异步、异步 Page720~721