Offer必备算法_滑动窗口_八道力扣OJ题详解（由浅到深）
目录
滑动窗口算法介绍
????????滑动窗口算法（Sliding Window Algorithm）是一种常见的算法技巧，用于解决一些数组或字符串相关的问题。滑动窗口算法的本质是同向双指针，双指针算法已经在前面博客讲过了，所谓滑动窗口，顾名思义可以理解成是一个会滑动的窗口，每次记录下窗口的状态，再找出符合条件的适合的窗口。它可以将双层嵌套的循环问题，转换为单层遍历的循环问题。使用两个指针一左一右构成一个窗口，就可以将二维循环的问题转化成一维循环一次遍历，相当于通过旧有的计算结果对搜索空间进行剪枝，使时间复杂度从O（N^2）降低至O（N），比如经典字符串查找算法Rabin-Karp 指纹字符串查找算法，它本质上也使用了滑动窗口的思想，通过公式推导降低窗口滑动时计算子串哈希值的复杂度。
算法原理：
- 窗口大小：滑动窗口算法通过设定一个窗口的大小来解决问题。窗口通常是一个连续的子数组或子字符串。
- 初始化窗口：初始化窗口的起始位置，并根据问题需求设定窗口的大小。
- 移动窗口：通过移动窗口的起始位置，不断调整窗口的大小和位置，以找到满足问题条件的解。
- 更新解：根据窗口的移动和调整，更新问题的解，并记录或返回所需的结果。
应用场景：
- 最小/最大子数组/子字符串：寻找给定数组或字符串中满足特定条件的最小或最大的子数组或子字符串。
- 字符串匹配：在一个字符串中寻找另一个字符串的出现或满足特定条件的子串。
- 滑动窗口和哈希表结合：通过使用哈希表来优化滑动窗口算法，提高效率。
- 优化窗口大小：根据问题的特性，调整窗口大小以寻找最佳解。
算法通常步骤：
- 初始化窗口的起始位置和结束位置，使其满足问题的要求。
- 进入循环，不断移动窗口的起始位置和结束位置，直到窗口滑动到数组或字符串的末尾。
- 在每一次循环中，检查窗口内的元素是否满足问题的要求。如果满足条件，则更新解或执行其他操作。如果不满足条件，则继续移动窗口。
- 在移动窗口时，要更新窗口内的元素和相应的数据结构，以确保窗口的正确性。
- 重复步骤2到步骤4，直到遍历完整个数组或字符串，返回解或所需的结果。
①力扣209. 长度最小的子数组
难度 中等
给定一个含有?n?个正整数的数组和一个正整数?target?。
找出该数组中满足其总和大于等于?target?的长度最小的?连续子数组?[numsl, numsl+1, ..., numsr-1, numsr]?，并返回其长度。如果不存在符合条件的子数组，返回?0?。
示例 1：
输入：target = 7, nums = [2,3,1,2,4,3]
输出：2
解释：子数组?[4,3]?是该条件下的长度最小的子数组。
示例 2：
输入：target = 4, nums = [1,4,4] 输出：1
示例 3：
输入：target = 11, nums = [1,1,1,1,1,1,1,1] 输出：0
提示：
1 <= target <= 10^91 <= nums.length <= 10^51 <= nums[i] <= 10^5
进阶：
- 如果你已经实现?
O(n)?时间复杂度的解法, 请尝试设计一个?O(n log(n))?时间复杂度的解法。
class Solution {
public:
int minSubArrayLen(int target, vector<int>& nums) {
}
};解析及代码
首先想到的是暴力枚举，定义两个指针和一个变量，可以做到时间为O（N^2）。
由于此问题分析的对象是一段连续的区间，因此可以考虑滑动窗口的思想来解决这道题。
本题为变长的滑动窗口，其窗口大小由target决定（窗口总和大于等于target），所以定义一个变量（窗口内总和），小于target右指针右移，大于target左指针右移，等于记录更新窗口大小即可。
i 位置开始，窗口内所有元素的和小于 target让滑动窗口满足：(那么当窗口内元素之和第一次大于等于目标值的时候，就是 i 位置开始，满足条件的最小长度)
做法：将右端元素划入窗口中，统计出此时窗口内元素的和：如果窗口内元素之和大于等于 target : 更新结果，并且将左端元素划出去的同时继续判断是否满足条件并更新结果(因为左端元素可能很小，划出去之后依旧满足条件，如果窗口内元素之和不满足条件：right++ ，另下一个元素进入窗口。
class Solution {
public:
int minSubArrayLen(int target, vector<int>& nums) {
// 时间：O（N）
int n = nums.size(), ret = n + 1; // 返回值不可能超过数组长度
int sum = 0, left = 0, right = 0;
while(right < n)
{
sum += nums[right]; // 进窗口
while(sum >= target) // 判断
{
ret = min(ret, right - left + 1); // 更新结果
sum -= nums[left++]; // 出窗口 然后left++
}
++right; // 判断不符合了
}
return ret == n + 1 ? 0 : ret;
}
};为什么滑动窗口可以解决问题，并且时间复杂度更低?
本质是利用单调性规避了很多不必要的枚举。
这个窗口寻找的是：以当前窗口最左侧元素 （记为 left）为基准，符合条件的情况。也就是在这道题中，从 left?开始，满足区间和 sum >= target 时的最右侧 （记为right)）能到哪里。
我们既然已经找到从 left?开始的最优的区间，那么就可以大胆舍去? left?。但是如果继续像暴力枚举，重新开始统计第二个元素 后的和，势必会有大量重复的计算 （因为我们在求第一段区间的时候，已经算出很多元素的和了，这些和是可以在计算下次区间和的时候用上的）。
此时，rigth 的作用就体现出来了，我们只需将 left?这个值从 sum 中剔除。从right?这个元素开始，往后找满足的区间（此时 right?也有可能是满足的，因为 left?可能很小。 sum 剔除掉 left?之后，依旧满足大于等于target ）。这样就能省掉大量重复的计算。这样不仅能解决问题，而且效率也会大大提升时间复杂度：虽然代码是两层循环，但是 left 指针和 right 指针都是不回退的，两者最多都往后移动 N 次。因此时间复杂度是 0(N)。
②力扣3. 无重复字符的最长子串
难度 中等
给定一个字符串?s?，请你找出其中不含有重复字符的?最长子串?的长度。
示例?1:
输入: s = "abcabcbb"
输出: 3
解释: 因为无重复字符的最长子串是 "abc"，所以其长度为 3。
示例 2:
输入: s = "bbbbb"
输出: 1
解释: 因为无重复字符的最长子串是 "b"，所以其长度为 1。
示例 3:
输入: s = "pwwkew" 输出: 3 解释: 因为无重复字符的最长子串是?"wke"，所以其长度为 3。? 请注意，你的答案必须是 子串 的长度，"pwke"?是一个子序列，不是子串。
提示：
0 <= s.length <= 5 * 10^4s?由英文字母、数字、符号和空格组成
class Solution {
public:
int lengthOfLongestSubstring(string s) {
}
};解析及代码
- 研究的对象是一段连续的区间，因此继续使用「滑动窗口」思想来写。让滑动窗口满足：窗口内所有元素都是不重复的。
- 假设选择字符串中的第 left 个字符作为起始位置，并且得到了不包含重复字符的最长子串的结束位置为 right。那么当我们选择第 left+1个字符作为起始位置时，首先从 left+1到 right的字符显然是不重复的，并且由于少了原本的第 left个字符，可以尝试继续增大 right，直到右侧出现了重复字符为止，出现重复字符时，left指针可以直接移动到重复字符的右边。
- 那么使用两个指针表示字符串中的某个子串的左右边界。其中左指针代表着上文中「枚举子串的起始位置」，而右指针即为上文中的 right；
在每一步的操作中，会将左指针向右移动一格，表示开始枚举下一个字符作为起始位置，然后可以不断地向右移动右指针，但需要保证这两个指针对应的子串中没有重复的字符。在移动结束后，这个子串就对应着以左指针开始的，不包含重复字符的最长子串。记录下这个子串的长度。- 在枚举结束后，找到的最长的子串的长度即为答案。
这里可以借助哈希的思想：
右端X元素进入窗口的时候，哈希表统计这个字符的频次：
如果这个字符出现的频次超过1，说明窗口内有重复元素，那么就从左侧开始划出窗口，
直到X这个元素的频次变为1，然后再更新结果。
如果没有超过1， 说明当前窗口没有重复元素，可以直接更新结果。
class Solution {
public:
int lengthOfLongestSubstring(string s) {
// 时间O（N）， 空间O（1）
int hash[128] = { 0 }; // 数组模拟哈希表->s由英文字母、数字、符号和空格组成
int n = s.size(), ret = 0, left = 0, right = 0;
while(right < n)
{
hash[s[right]]++; // 进窗口->进入哈希表
while(hash[s[right]] > 1)
{
hash[s[left++]]--; // 出窗口->哈希表的值减减然后left加加
}
ret = max(ret, right - left + 1); // 更新结果
++right; // 下一个元素进入窗口
}
return ret;
}
};③力扣1004. 最大连续1的个数 III
1004. 最大连续1的个数 III - 力扣（LeetCode）
难度 中等
给定一个二进制数组?nums?和一个整数?k，如果可以翻转最多?k?个?0?，则返回?数组中连续?1?的最大个数?。
示例 1：
输入：nums = [1,1,1,0,0,0,1,1,1,1,0], K = 2 输出：6 解释：[1,1,1,0,0,1,1,1,1,1,1] 粗体数字从 0 翻转到 1，最长的子数组长度为 6。
示例 2：
输入：nums = [0,0,1,1,0,0,1,1,1,0,1,1,0,0,0,1,1,1,1], K = 3 输出：10 解释：[0,0,1,1,1,1,1,1,1,1,1,1,0,0,0,1,1,1,1] 粗体数字从 0 翻转到 1，最长的子数组长度为 10。
提示：
1 <= nums.length <= 10^5nums[i]?不是?0?就是?10 <= k <= nums.length
class Solution {
public:
int longestOnes(vector<int>& nums, int k) {
}
};解析及代码
此题可转化为找出最长子数组，子数组0的个数不超过K个，就和前两篇滑动窗口的题目一样了。
设置计数器，计算0的个数
首先数组不能越界，所以最外层循环进入条件为right<n（数组长度）
滑动窗口四步走：
- 进窗口，遇到0计数器++，否则忽略（ ps：滑动窗口的进窗口操作是载入数据，而不是单纯的移动right指针，如果只移动了right而没有对数据进行处理，则不算进窗口。）
- 判断，0个数是否大于 题目中的k （不是等于而是大于，这是因为如果在计数器的0个数等于k时就停止进窗口，并更新状态，那么就会漏情况。比如k为2 那么数组 1 ?1 ?0 ?0 ?1 ?1 ?1 1 这个数组中最长子串的长度就是8，如果是在0等于2个时就停下，那么更新的结果就会是4。）
- 出窗口，left移动，遇到0时计数器--，直到计数器的0个数等于k个，符合题目要求为止。
- 更新结果，无论是否出窗口都更新状态。只要用个max函数来判断此时的子串是否是最大长度即可。
class Solution {
public:
int longestOnes(vector<int>& nums, int k) {
// 时间O（N）， 空间O（1）
int n = nums.size(), ret = 0, left = 0, right = 0, zero = 0;
while(right < n)
{
if(nums[right] == 0)
{
zero++; // 进窗?
}
while(zero > k) // 判断
{
if(nums[left++] == 0)
{
zero--; // 出窗?
}
}
ret = max(ret, right - left + 1); // 更新结果
++right;
}
return ret;
}
};④力扣1658. 将x减到0的最小操作数
1658. 将 x 减到 0 的最小操作数 - 力扣（LeetCode）
难度 中等
给你一个整数数组?nums?和一个整数?x?。每一次操作时，你应当移除数组?nums?最左边或最右边的元素，然后从?x?中减去该元素的值。请注意，需要?修改?数组以供接下来的操作使用。
如果可以将?x?恰好?减到?0?，返回?最小操作数?；否则，返回?-1?。
示例 1：
输入：nums = [1,1,4,2,3], x = 5 输出：2 解释：最佳解决方案是移除后两个元素，将 x 减到 0 。
示例 2：
输入：nums = [5,6,7,8,9], x = 4 输出：-1
示例 3：
输入：nums = [3,2,20,1,1,3], x = 10 输出：5 解释：最佳解决方案是移除后三个元素和前两个元素（总共 5 次操作），将 x 减到 0 。
提示：
1 <= nums.length <= 10^51 <= nums[i] <= 10^41 <= x <= 10^9
class Solution {
public:
int minOperations(vector<int>& nums, int x) {
}
};解析及代码
转化成了最长子数组的长度，所有元素的和正好等于数组和 - x。
题意是从两边找几个数，使其的和等于x，从两边找的话很难，因为有时候删左边，有时候删右边，所以“正难则反”，可以找中间有没有等于数组和 - x的区间，这样两边的和就是x了。
class Solution {
public:
int minOperations(vector<int>& nums, int x) {
// 时间O（N）， 空间O（1）
int tmp = 0;
for(auto& e : nums)
{
tmp += e;
}
int target = tmp - x;
if(target < 0)
{
return -1;
}
int n = nums.size(), len = -1, sum = 0, left = 0, right = 0;
while(right < n) // 找最大子数组的和，长度为len
{
sum += nums[right];
while(sum > target) // 判断
{
sum -= nums[left++]; // 出窗口 然后left++
}
if(sum == target)
{
len = max(len, right - left + 1); // 更新结果
}
++right; // 判断不符合了
}
return len == -1 ? len : (n - len);
}
};⑤力扣904. 水果成篮
难度 中等
你正在探访一家农场，农场从左到右种植了一排果树。这些树用一个整数数组?fruits?表示，其中?fruits[i]?是第?i?棵树上的水果?种类?。
你想要尽可能多地收集水果。然而，农场的主人设定了一些严格的规矩，你必须按照要求采摘水果：
- 你只有?两个?篮子，并且每个篮子只能装?单一类型?的水果。每个篮子能够装的水果总量没有限制。
- 你可以选择任意一棵树开始采摘，你必须从?每棵?树（包括开始采摘的树）上?恰好摘一个水果?。采摘的水果应当符合篮子中的水果类型。每采摘一次，你将会向右移动到下一棵树，并继续采摘。
- 一旦你走到某棵树前，但水果不符合篮子的水果类型，那么就必须停止采摘。
给你一个整数数组?fruits?，返回你可以收集的水果的?最大?数目。
示例 1：
输入：fruits = [1,2,1] 输出：3 解释：可以采摘全部 3 棵树。
示例 2：
输入：fruits = [0,1,2,2] 输出：3 解释：可以采摘 [1,2,2] 这三棵树。 如果从第一棵树开始采摘，则只能采摘 [0,1] 这两棵树。
示例 3：
输入：fruits = [1,2,3,2,2] 输出：4 解释：可以采摘 [2,3,2,2] 这四棵树。 如果从第一棵树开始采摘，则只能采摘 [1,2] 这两棵树。
示例 4：
输入：fruits = [3,3,3,1,2,1,1,2,3,3,4] 输出：5 解释：可以采摘 [1,2,1,1,2] 这五棵树。
提示：
1 <= fruits.length <= 10^50 <= fruits[i] < fruits.length
class Solution {
public:
int totalFruit(vector<int>& fruits) {
}
};解析及代码1（使用容器）
研究的对象是?段连续的区间，可以使用「滑动窗口」思想来解决问题。
让滑动窗口满足：窗口内水果的种类只有两种。
做法：右端水果进入窗口的时候，用哈希表统计这个水果的频次。这个水果进来后，判断哈希表的大小：
如果大小超过2：说明窗口内水果种类超过了两种。那么就从左侧开始依次将水果划出窗口，直到哈希表的大小小于等于2，然后更新结果
如果没有超过2：说明当前窗口内水果的种类不超过两种，直接更新结果 ret
class Solution {
public:
int totalFruit(vector<int>& fruits) {
unordered_map<int, int> hash;
int ret = 0, left = 0, right = 0;
while(right < fruits.size())
{
hash[fruits[right]]++; // 进窗口
while(hash.size() > 2) // 判断
{
hash[fruits[left]]--; // 出窗口
if(hash[fruits[left]] == 0)
{
hash.erase(fruits[left]);
}
++left;
}
ret = max(ret, right - left + 1);
++right;
}
return ret;
}
};
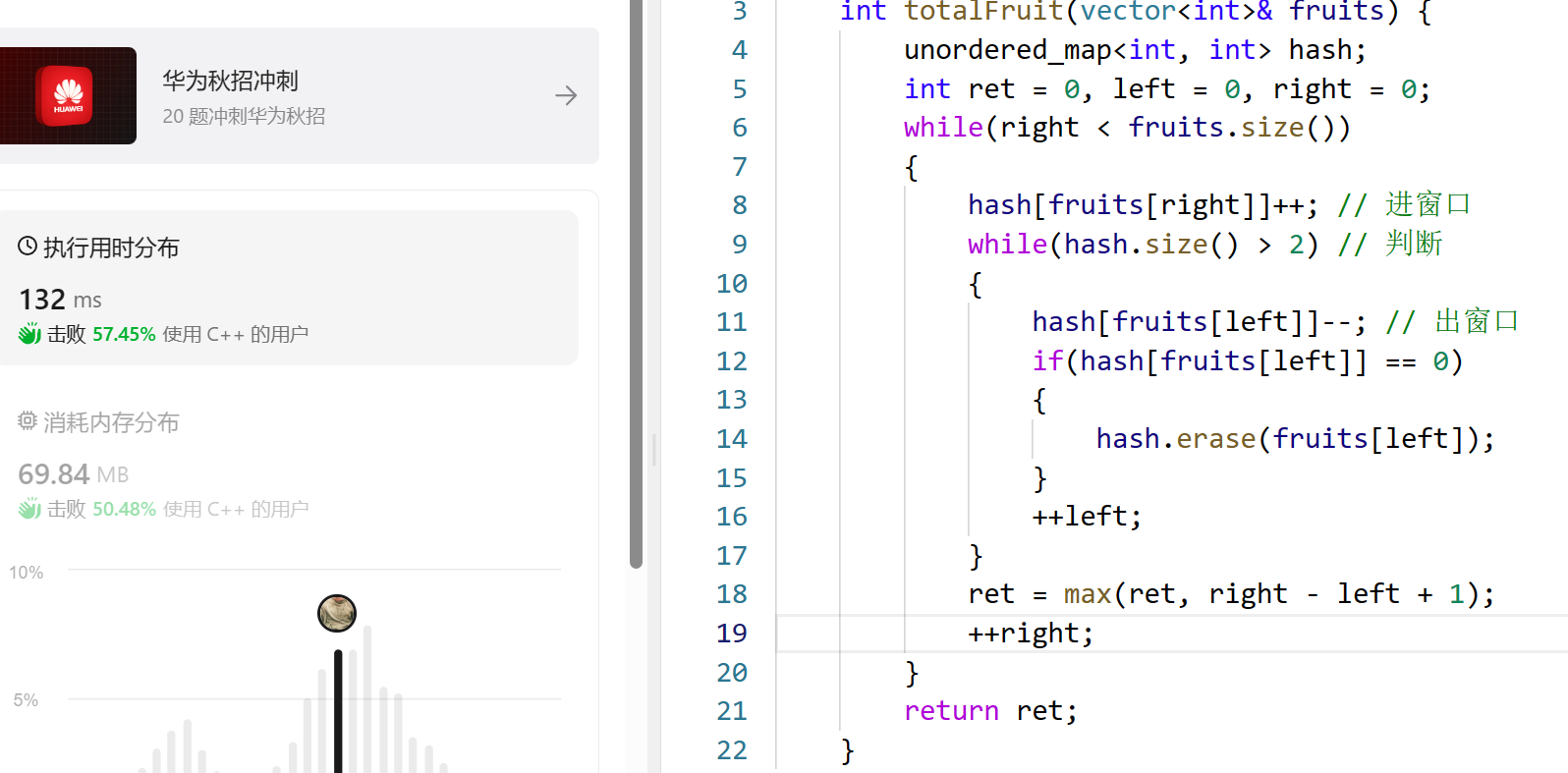
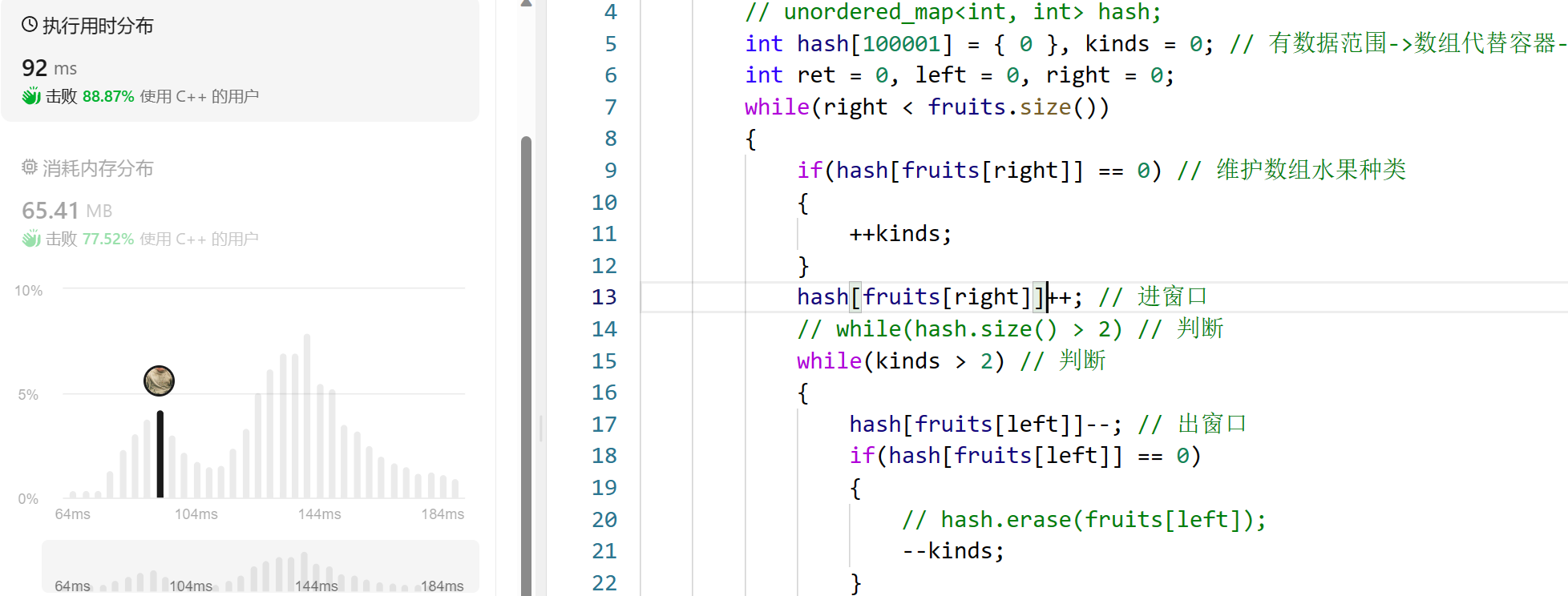
解析及代码2（开数组）
可以看到上面的代码的通过效率还是很差的，因为容器的删除耗了时间，注意到这题的范围，此时就可以开一个数组来代替容器：
class Solution {
public:
int totalFruit(vector<int>& fruits) {
// unordered_map<int, int> hash;
int hash[100001] = { 0 }, kinds = 0; // 有数据范围->数组代替容器->提高效率
int ret = 0, left = 0, right = 0;
while(right < fruits.size())
{
if(hash[fruits[right]] == 0) // 维护数组水果种类
{
++kinds;
}
hash[fruits[right]]++; // 进窗口
// while(hash.size() > 2) // 判断
while(kinds > 2) // 判断
{
hash[fruits[left]]--; // 出窗口
if(hash[fruits[left]] == 0)
{
// hash.erase(fruits[left]);
--kinds;
}
++left;
}
ret = max(ret, right - left + 1);
++right;
}
return ret;
}
};此时效率就会提高一些。
⑥力扣438. 找到字符串中所有字母异位词
438. 找到字符串中所有字母异位词 - 力扣（LeetCode）
难度 中等
给定两个字符串?s?和?p，找到?s?中所有?p?的?异位词?的子串，返回这些子串的起始索引。不考虑答案输出的顺序。
异位词?指由相同字母重排列形成的字符串（包括相同的字符串）。
示例?1:
输入: s = "cbaebabacd", p = "abc" 输出: [0,6] 解释: 起始索引等于 0 的子串是 "cba", 它是 "abc" 的异位词。 起始索引等于 6 的子串是 "bac", 它是 "abc" 的异位词。
?示例 2:
输入: s = "abab", p = "ab" 输出: [0,1,2] 解释: 起始索引等于 0 的子串是 "ab", 它是 "ab" 的异位词。 起始索引等于 1 的子串是 "ba", 它是 "ab" 的异位词。 起始索引等于 2 的子串是 "ab", 它是 "ab" 的异位词。
提示:
1 <= s.length, p.length <= 3 * 10^4s?和?p?仅包含小写字母
class Solution {
public:
vector<int> findAnagrams(string s, string p) {
}
};解析及代码1
首先用两个数组做哈希表敲出来的代码：
class Solution {
public:
vector<int> findAnagrams(string s, string p) {
int hash1[26] = { 0 }, hash2[26] = { 0 };
for (auto& e : p)
{
hash2[e - 'a']++;
}
int left = 0, right = 0, n1 = s.size(), n2 = p.size();
vector<int> ret;
if(n2 > n1)
return ret;
while (right < n2)
{
hash1[s[right++] - 'a']++;
}
while (right < n1)
{
int j = 0;
for (; j < 26; ++j)
{
if (hash1[j] != hash2[j])
{
break;
}
}
if (j == 26)
{
ret.push_back(left);
}
hash1[s[right++] - 'a']++;
hash1[s[left++] - 'a']--;
}
int j = 0;
for (; j < 26; ++j) // 再判断一遍
{
if (hash1[j] != hash2[j])
{
break;
}
}
if (j == 26)
{
ret.push_back(left);
}
return ret;
}
};解析及代码2
改进：用一个变量count维护判断逻辑
class Solution {
public:
vector<int> findAnagrams(string s, string p) {
int hash1[26] = { 0 }, hash2[26] = { 0 };
for (auto& e : p)
{
hash2[e - 'a']++;
}
int left = 0, right = 0, n1 = s.size(), n2 = p.size(), count = 0;
vector<int> ret;
if(n2 > n1)
return ret;
while (right < n1)
{
char in = s[right];
if(++hash1[in - 'a'] <= hash2[in - 'a'])
{
++count; // 进窗口和维护count
}
if(right - left + 1 > n2) // 判断
{
char out = s[left++];
if(hash1[out - 'a']-- <= hash2[out - 'a'])
{
--count; // 出窗口和维护count
}
}
if (count == n2) // 更新结果
{
ret.push_back(left);
}
++right;
}
return ret;
}
};⑦力扣30. 串联所有单词的子串
难度 困难
给定一个字符串?s?和一个字符串数组?words。?words?中所有字符串?长度相同。
?s?中的?串联子串?是指一个包含??words?中所有字符串以任意顺序排列连接起来的子串。
- 例如，如果?
words = ["ab","cd","ef"]， 那么?"abcdef"，?"abefcd"，"cdabef"，?"cdefab"，"efabcd"， 和?"efcdab"?都是串联子串。?"acdbef"?不是串联子串，因为他不是任何?words?排列的连接。
返回所有串联子串在?s?中的开始索引。你可以以?任意顺序?返回答案。
示例 1：
输入：s = "barfoothefoobarman", words = ["foo","bar"]
输出：[0,9]
解释：因为 words.length == 2 同时 words[i].length == 3，连接的子字符串的长度必须为 6。
子串 "barfoo" 开始位置是 0。它是 words 中以 ["bar","foo"] 顺序排列的连接。
子串 "foobar" 开始位置是 9。它是 words 中以 ["foo","bar"] 顺序排列的连接。
输出顺序无关紧要。返回 [9,0] 也是可以的。
示例 2：
输入：s = "wordgoodgoodgoodbestword", words = ["word","good","best","word"]
输出：[]
解释：因为 words.length == 4 并且 words[i].length == 4，所以串联子串的长度必须为 16。
s 中没有子串长度为 16 并且等于 words 的任何顺序排列的连接。
所以我们返回一个空数组。
示例 3：
输入：s = "barfoofoobarthefoobarman", words = ["bar","foo","the"] 输出：[6,9,12] 解释：因为 words.length == 3 并且 words[i].length == 3，所以串联子串的长度必须为 9。 子串 "foobarthe" 开始位置是 6。它是 words 中以 ["foo","bar","the"] 顺序排列的连接。 子串 "barthefoo" 开始位置是 9。它是 words 中以 ["bar","the","foo"] 顺序排列的连接。 子串 "thefoobar" 开始位置是 12。它是 words 中以 ["the","foo","bar"] 顺序排列的连接。
提示：
1 <= s.length <= 10^41 <= words.length <= 50001 <= words[i].length <= 30words[i]?和?s?由小写英文字母组成
class Solution {
public:
vector<int> findSubstring(string s, vector<string>& words) {
}
};解析及代码
此题和上一题力扣438题思路类似，也是滑动窗口+哈希表，比较考验容器的使用，用一个变量count维护判断逻辑。
class Solution {
public:
vector<int> findSubstring(string s, vector<string>& words) {
vector<int> ret;
unordered_map<string, int> hash2; // 保存 words ??所有单词的频次
for (auto& e : words)
{
hash2[e]++;
}
int len = words[0].size(), m = words.size();
for (int i = 0; i < len; i++) // 执? len 次
{
int left = i, right = i, count = 0;
unordered_map<string, int> hash1; // 维护窗?内单词的频次
while (right + len <= s.size())
{
string in = s.substr(right, len); // 进窗? + 维护 count
hash1[in]++;
if (hash2.count(in) && hash1[in] <= hash2[in])
{
count++;
}
if (right - left + 1 > len * m) // 判断
{
// 出窗? + 维护 count
string out = s.substr(left, len);
if (hash2.count(out) && hash1[out] <= hash2[out])
{
count--;
}
hash1[out]--;
left += len;
}
if (count == m) // 更新结果
{
ret.push_back(left);
}
right += len;
}
}
return ret;
}
};⑧力扣76. 最小覆盖子串
难度 困难
给你一个字符串?s?、一个字符串?t?。返回?s?中涵盖?t?所有字符的最小子串。如果?s?中不存在涵盖?t?所有字符的子串，则返回空字符串?""?。
注意：
- 对于?
t?中重复字符，我们寻找的子字符串中该字符数量必须不少于?t?中该字符数量。 - 如果?
s?中存在这样的子串，我们保证它是唯一的答案。
示例 1：
输入：s = "ADOBECODEBANC", t = "ABC" 输出："BANC" 解释：最小覆盖子串 "BANC" 包含来自字符串 t 的 'A'、'B' 和 'C'。
示例 2：
输入：s = "a", t = "a" 输出："a" 解释：整个字符串 s 是最小覆盖子串。
示例 3:
输入: s = "a", t = "aa" 输出: "" 解释: t 中两个字符 'a' 均应包含在 s 的子串中， 因此没有符合条件的子字符串，返回空字符串。
提示：
m == s.lengthn == t.length1 <= m, n <= 105s?和?t?由英文字母组成- 进阶：你能设计一个在?
o(m+n)?时间内解决此问题的算法吗？
class Solution {
public:
string minWindow(string s, string t){
}
};解析及代码
此题和上篇力扣30题思路类似，也是滑动窗口+哈希表，用一个变量count维护判断逻辑。
class Solution {
public:
string minWindow(string s, string t){
int hash1[128] = { 0 }; // 统计字符串 t 中每?个字符的频次
int kinds = 0; // 统计有效字符有多少种
for (auto& e : t)
{
if (hash1[e]++ == 0)
{
kinds++;
}
}
int hash2[128] = { 0 }; // 统计窗?内每个字符的频次
int minlen = INT_MAX, begin = -1;
for (int left = 0, right = 0, count = 0; right < s.size(); right++)
{
char in = s[right];
if (++hash2[in] == hash1[in]) // 进窗? + 维护 count
{
count++;
}
while (count == kinds) // 判断条件
{
if (right - left + 1 < minlen) // 更新结果
{
minlen = right - left + 1;
begin = left;
}
char out = s[left++];
if (hash2[out]-- == hash1[out]) // 出窗? + 维护 count
{
count--;
}
}
}
return begin == -1 ? "" : s.substr(begin, minlen);
}
};本篇完。
下一部分是二分查找算法的讲解和刷题。
本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符，请联系我的编程经验分享网邮箱：chenni525@qq.com进行投诉反馈，一经查实，立即删除！
- Python教程
- 深入理解 MySQL 中的 HAVING 关键字和聚合函数
- Qt之QChar编码（1）
- MyBatis入门基础篇
- 用Python脚本实现FFmpeg批量转换
- 应用架构演变过程、rpc及Dubbo简介
- 清华大模型Chatglm2-6B的微调方法和微调模型使用方式（非常仔细，值得借鉴）
- LeetCode 热题100——单调栈
- C语言爬虫程序编写的爬取APP通用模板
- 远程登录Linux服务器：命令+工具版
- leetcode 141 判断链表中是否存在环
- 1.13寒假集训
- burpsuite专业版的安装和破解（2024年最新）
- 20240104确认AIO-3399J的开发板适配ov13850摄像头不支持4K分辨率录像
- 主题-----读微信公众号