梯度下降算法 寻找函数最小值 找最快下山路线 python写个梯度下降算法示例

梯度下降算法是一种用于寻找函数最小值的优化算法。

它在机器学习和深度学习中被广泛使用，特别是在训练神经网络时。我们可以通过一个简单的生活中的例子来理解它：

想象你在一座山上，需要找到最快的路线下山。你不能一眼看到最低点，但你可以感受到脚下的坡度。梯度下降的思路就是在当前位置寻找坡度最陡的方向，并朝这个方向走一小步，然后重复这个过程，直到你到达山谷，也就是你不能再下降了。

在数学中，这座“山”就是你想要最小化的函数。梯度表示的是函数在当前位置的坡度或者说变化率。梯度下降算法就是沿着梯度的反方向，即最陡峭的下降方向，逐步调整参数，直到找到函数的最小值。

在机器学习中，这个最小值通常代表着最佳的模型参数，比如最小化损失函数以提高模型的预测准确性。

梯度下降算法有几个变体，如随机梯度下降（SGD）、小批量梯度下降（Mini-batch Gradient Descent）和批量梯度下降（Batch Gradient Descent），它们主要在于如何选择和处理数据点以计算梯度。

python写个梯度下降算法示例

import numpy as np
import matplotlib.pyplot as plt

# 定义一个简单的二次函数 f(x) = x^2
def function(x):
    return x ** 2

# 定义函数的梯度 g(x) = 2x
def gradient(x):
    return 2 * x

# 梯度下降算法
def gradient_descent(starting_point, learning_rate, num_iterations):
    x = starting_point
    x_history = [x]
    for i in range(num_iterations):
        grad = gradient(x)
        x = x - learning_rate * grad
        x_history.append(x)
    return x_history

# 参数设置
starting_point = 10  # 初始点
learning_rate = 0.1  # 学习率
num_iterations = 50  # 迭代次数

# 运行梯度下降算法
x_history = gradient_descent(starting_point, learning_rate, num_iterations)

# 绘制梯度下降过程
x_values = np.linspace(-11, 11, 400)
y_values = function(x_values)
plt.plot(x_values, y_values, label='f(x) = x^2')
plt.scatter(x_history, function(np.array(x_history)), color='red', marker='o')
plt.title('Gradient Descent Optimization')
plt.xlabel('x')
plt.ylabel('f(x)')
plt.legend()
plt.show()

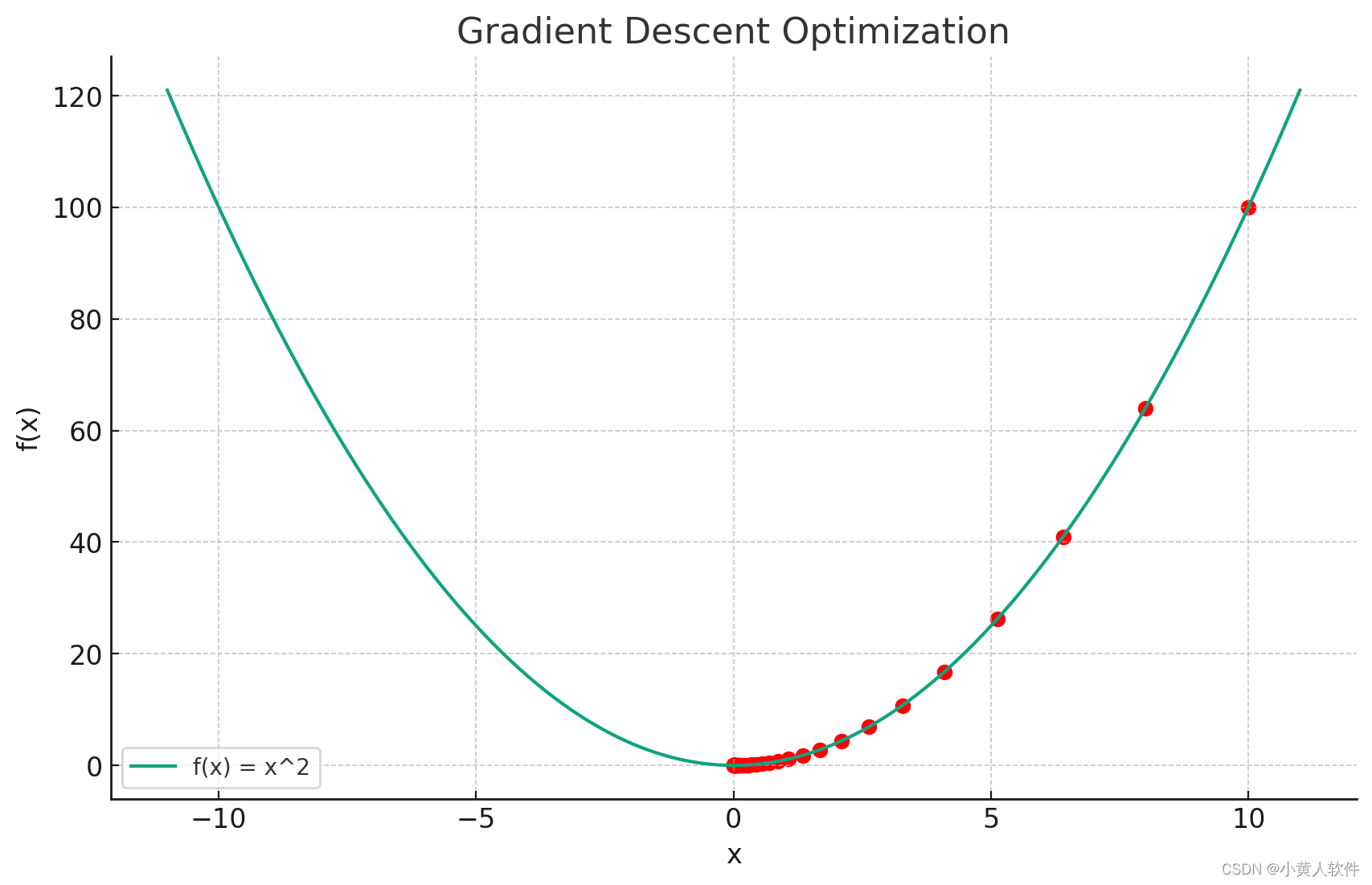
上面的Python代码展示了一个简单的梯度下降算法示例。这个例子中，我们试图找到函数 ( f(x) = x^2 ) 的最小值。

1. 函数和梯度的定义：首先，我们定义了函数 ( f(x) = x^2 ) 和它的梯度 ( g(x) = 2x )。

2. 梯度下降算法：然后，我们实现了梯度下降算法。这个算法从一个初始点开始，重复应用梯度下降步骤（当前点减去学习率乘以梯度），直到达到指定的迭代次数。

3. 参数设置：我们设定初始点为 10，学习率为 0.1，迭代次数为 50。

4. 结果可视化：最后，我们绘制了函数 ( f(x) ) 和梯度下降过程中的点。在图中，红色点表示每一步迭代后的位置，可以看到随着迭代进行，点逐渐接近函数的最小值点（即 ( x = 0 ) 处）。

这个示例简单展示了梯度下降算法的基本原理和实现方式。在实际应用中，这个算法通常用于更复杂的函数和多维参数空间。