【算法设计与分析】汇总

目录

绪论

分治法

动态规划法

贪心法

回溯法

分支限界法

随机化算法

---

绪论

算法概述：算法是指解决问题的一种方法或过程。（由若干条指令组成的有穷序列）
(1)输入有零个或多个由外部提供的量作为算法的输入。
(2)输出: 算法产生至少一个量作为输出。
(3)确定性: 组成算法的每条指令是清晰的，无歧义的。
(4)有限性: 算法中每条指令执行次数是有限的，执行每条指令的时间也是有限的。

一个算法的复杂性的高低体现在运行该算法所需的计算机资源 (主要指时间和空间资源)的多少上。算法的复杂性分为: 时间复杂性和空间复杂性。【最坏情况，最好情况，平均情况】

渐进符号：
1）渐进符号O：f(n)=O(g(n))当且仅当存在正的常数 C和n0，使得对于所有的n≥?n0，有f(n)≤?Cg(n)。此时，称 g(n)是f(n)当 n 充分大时的一个上界。
2）渐近记号?Ω：f(n)=?Ω(g(n)) 当且仅当存在正的常数 C和n0使得对于所有的n ≥ n0，有f(n)≥Cgn)。此时，称 g(n)是 f(n)当 n 充分大时的一个下界
3）渐近记号θ ：f(n)=θ?(g(n))当且仅当存在正的常数 C1，C2和n0，使得对于所有的n≥n0，有C1g(n)≤f(n)≤ ?C2g(n)。 此时，称f(n)与g(n)同阶
4）渐进记号小 o:f(n)=o(g(n))当且仅当 f(n)=O(g(n))和 g(n)?≠ O(f(n))，此时g(n)是 f(n)的一个绝对上界。
5）渐进记号小ω:f(n)=ω(g(n))当且仅当 f(n)=Ω(g(n))和 g(n)?≠?Ω(f(n))，此时g(n)是 f(n)的一个绝对下界。

1. 衡量一个算法好坏的标准是（）C
   A、运行速度快慢 B、占空间大小 C、时间复杂度高低 D、代码长度
2. 算法的复杂性有 时间复杂度 和空间复杂度。
3. 求下列函数的渐进表达式。
   n^3 + 100n + 3 => O(n^3)
   2 ^ n + 10n^2 = > O(2^n)
4. 选出最低复杂度的选项（）D
   A、O(n^3) B、O(n2 log n) C、O(n2) D、O(nlogn)
5. 算法分析的目的是（）C
   A、找出数据结构的合理性 B、研究算法中的输入和输出关系
   C、分析算法的效率以求改进 D、分析算法的易懂性和文档性
6. 算法分析的两个主要方面是（）B
   A、正确性和简明性 B、空间复杂性和时间复杂性 C、可读性和文档性 D、数据复杂性和程序复杂性

分治法

基本思想：将一个规模为 n 的问题分解为 k 个规模为较小的子问题，这些子问题互相独立且与原问题相同。递归地求解这些子问题，然后利用子问题的解合并(构造) 出原问题的解。

算法设计：
1）分解阶段：将整个问题划分为多个子问题；
2）递归求解阶段：递归调用算法，求解每个子问题
3）合并阶段：合并子问题的解，形成原始问题的解

1. 使用分治法求解不需要满足的条件是：A
   A、子问题必须是一样的 B、子问题不重复 C、子问题的解可以合并 D、原问题和子问题使用相同的方法解
2. 分治法的设计思想是将一个难以直接解决的大问题分割成规模较小的子问题，分别解决子问题，最后将子问题的解组合起来形成原问题的解，这要求原问题和子问题()。D
   A、问题规模相同，问题性质相同 B、问题规模不相同，问题性质不相同
   C、问题规模相同，问题性质不相同 D、问题规模不相同，问题性质相同
3. 不可以使用分治法求解的问题是（）。D
   A、棋盘覆盖 B、合并排序 C、快速排序 D、0-1背包
4. 有一个有序表位(1,3,9,12,32,41,45,62,75,77,82,95,991，当采用二分查找法查找关键字为82的元素时，第__C__次比较后查找成功。
   A、1 B、2 C、4 D、8
5. 分治法的适用条件：
   1）问题规模可以被分解为若干个较小的相同问题；
   2）子问题可以被独立解决；
   3）子问题的解可以合并为该问题的解；
   4）各个子问题是相互独立的，不存在公共的子问题。

动态规划法

基本思想：将要求解的问题一层一层地分解成一级一级、规模逐步缩小的子问题，指导可以直接求解其解的子问题为止。所有子问题按层次关系构成一棵子问题树。树根是原问题。原问题的解依赖子子问题树中所有子问题的解。

动态规划法通常用于求一个问题在某种意义下的最优解。适合采用动态规划方法的优化问题必须具备最优子结构性质和子问题重叠性质。当一个问题的优化解包含了子问题的优化解时，则称该问题具有优化子结构性质。

算法设计：
（1）分析最优解的性质，并刻画其结构特征
（2）递归地定义最优值(每个解都有一个值，代价).
（3）根据递归方程分解子问题，直到不能分为止。
（4）自底向上的方式计算最优值，并记录构造最优解所需的信息
（5）根据计算最优值时得到的信息，构造一个最优解。

常见问题：最长公共子序列问题，矩阵连乘最佳计算次序问题，最大子段和问题，0-1背包问题

最长公共子序列LCS：

基本思想：
1.从 b[m][n]开始按指针搜索;
2.若 b[i][j]=“↖”, 则xi=yj是 LCS 的一个元素;
3.如此找到的序列是X 与Y的 LCS 的反序。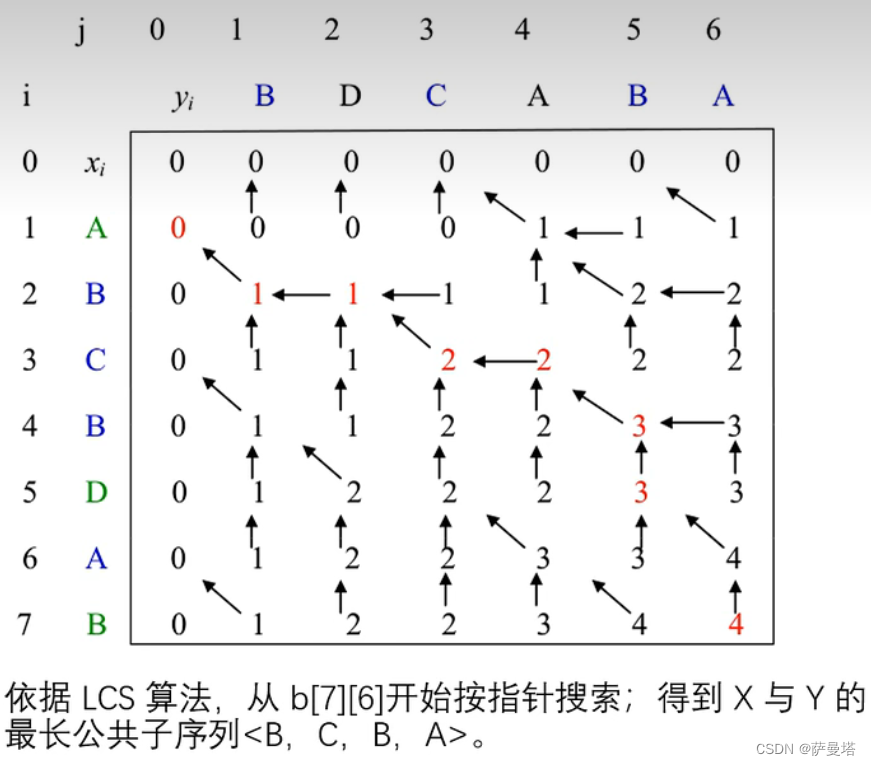

矩阵连乘最佳计算次序问题
将矩阵连乘积 Ai,(Ai+1)···Aj?简记为A[i:j], 计算 A[1:n]的一个最优次序。
问题关键特征: 计算 A[1:n]的一个最优次序所包含的计算 A[1:k]和A[k+1:n]的次序也是最优的。
m[i][j]记录A[i:j]所需的最少数乘次数，即最优值


构造最优解：
最优计算次序 ((A1 (A2A3)) ((A4A5)A6))
计算出所要求的连乘积A1A2A3A4A5A6
构造最优解的时间为 O(n)。

0-1背包问题
递归式：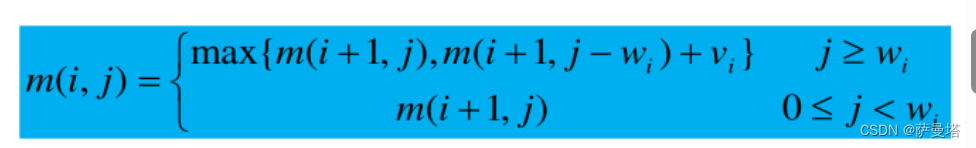

1. 动态规划算法的基本要素为（）C
   A、最优子结构与贪心选择 B、重叠子问题与贪心选择 C、最优子结构与重叠子问题 D、预排序与递归调用
2. 下列算法中通常以自底向上的方式求解最优解的是（）B
   A、备忘录 B、动态规划 C、贪心算法 D、回溯法
3. 若序列X={B,C,A,D,B,C,D}，Y={A,C,B,A,B,D,C,D}，请给出序列X和Y的最长公共子序列 BABCD 、CABCD 、CADCD 。（填写字符串即可）
4. 动态规划的设计思想：将原问题分解成若干个子问题，先求解子问题，再从这些子问题的解得到原问题的解
5. 下列是动态规划算法基本要素的是（ A ）。
   A、重叠子问题 B、构造最优解 C、算出最优解 D、定义最优解
6. 所求解的问题满足 __D__ 是使用动态规划算法的必要条件。
   A、子问题重叠 B、子问题互相独立 C、多米诺性质 D、最优子结构性质（优化原则）

7. 动态规划与分治法在分解子问题方面的不同点是 子问题的独立性 。

贪心法

基本思想：求解组合 (最) 优化问题的贪心算法包含一系列步骤。每一步都在一组选择中做出在当前看来最好的选择，希望通过做出局部优化选择达到全局优化选择。但贪心算法不一定总产生优化解，所以一个贪心算法是否产生优化解，需要严格证明。

贪心法求解的问题必须具有最优子结构和贪心选择性，贪心算法是按局部优化选择的。
常见问题：活动安排问题，最优装载问题，背包问题

1. 通常以自顶向下的方式求解最优解的是( )。A
   A、贪心算法 B、回溯法 C、动态规划 D、分支限界
2. 下面问题不能使用贪心法解决是 B
   A、单源最短路 B、N皇后问题 C、最小花费生成树问题 D、背包问题
3. __贪心选择___________是贪心算法可行的第一个基本要素，也是贪心算法与动态规划算法的主要区别。
4. 哈夫曼编码的贪心算法所需的计算时间为_____.B
   A、O(n 2n) B、O(nlogn) C、O(2n) D、O(n)
5. 采用贪心算法的最优装载问题的主要计算量在于将集装箱依其重量从小到大排序，故算法的时间复杂度为 B
   A、O(n 2n) B、O(nlogn) C、O(2n) D、O(n)
6. 用于求最小生成树的Prim算法和Kruskal算法都是基于思想设计的算法 C
   A.分治法 B.穷举法 C.贪心算法 D.回溯法
7. 贪心算法总是做出在当前看来___最优______的选择。也就是说贪心算法并不从整体最优考虑，它所做出的选择只是在某种意义上的_____局部最优_________。
8. 贪心算法的基本要素是 贪心选择 性质和 最优子结构 性质。

回溯法

基本思想：在包含问题所有解的解空间树中，按照深度优先的策略，从根出发进行搜索。搜索每到达解空间树的一个结点，总是先判断以该结点为根的子树 (或结点) 是否肯定不包含问题的解。如果肯定不包含，则跳过对该子树的系统搜索，一层一层地向它的祖先回溯，直到遇上一个还有未被搜索过的儿子的结点，才转向该结点的一个未曾搜索过的儿子结点，继续搜索;否则，进入该子树，继续按深优先的策略进行搜索。

常见问题：N皇后问题，图的M着色问题，批处理作业调度问题

1. 回溯法在问题的解空间中，按（ ）策略，从根结点出发搜索解空间。D
   A、广度优先 B、活结点优先 C、扩展结点优先 D、深度优先
2. 0-1背包问题的回溯算法所需的计算时间为（ ）C
   A、O(2n) B、O(nlogn) C、O(n2n) D、O(n)
3. 回溯法的效率不依赖于以下哪一个因素？（ ）C
   A、产生x[k]的时间 B、满足显约束的x[k]值的个数 C、问题的解空间 D、计算上界函数bound的时间

分支限界法

基本思想：分支限界算法是一种用于求解组合优化问题的算法策略。它的主要思想是将问题分解为部分子问题，通过对子问题的求解来逐步逼近问题的最优解。一般包含以下几点
1、分支策略:算法将问题分解为若干个子问题，这些子问题进一步分解，形成问题的解空间树。
2、限界策略:在解空间树上为每一个子问题定义一个上界或下界，用于判断该子问题是否可能包含问题的最优解。如果一个子问题的界限值比已知的最优解还要差，那么这个子问题就不必再进一步考虑。
3、广度优先和深度优先:分支限界算法可以采用广度优先策略或深度优先策略来遍历解空间树。
4、活节点:在算法执行过程中，尚未被排除且尚未求解的子问题称为活节点。算法维护一个活节点表，用于记录当前的活节点。
5、求解整数优化问题:分支限界算法常用于求解整数线性规划问题和一些组合优化问题。

常见分支限界法：
1）队列式分支限界：队列式分支限界法将活结点表组织成一个队列，并按照队列先进先出 (FIFO) 原则选取下一个结点为扩展结点。
2）(2) 优先队列式分支限界法：优先队列式分支限界法的主要特点是将活结点表组组成一个优先队列(用堆实现)，并选取优先级最高的活结点成为当前扩展结点。

1. 常见的两种分支限定法为( )。D
   A、广度优先分支限定与深度优先分支限定 B、队列式(FIFO)分支限定与堆栈式分支限定
   C、排列树与子集树 D、队列式分支限定与优先级分支限定
2. 优先级队列式分支限界法选取扩展结点的原则是（ ）。C
   A、先进先出 B、随机 C、结点的优先级 D、后进先出
3. 在对问题的解空间树进行搜索的方法中，一个活结点最多有一次机会成为活结点的是（B）。
   A、回溯法 B、分支限界法 C、回溯法和分支限界法 D、回溯法求解子集树问题
4. 下面不是分支界限法的是（）D
   A、广度优先 B、最小耗费优先 C、最大效益优先 D、深度优先

随机化算法

1.?数值概率算法：常用于求解数值问题。这类算法所得到的往往是近似解，且近似解的精度随计算时间的增加而不断提高。在许多情况下，要计算出问题的精确解是不可能或没有必要的。

2.?蒙特卡罗算法：常用于求解问题的精确解，用蒙特卡罗算法总能求得问题的一个解，但这个解未必是正确的(可能会偶尔地产生一个不正确的答案）。

3.拉斯维加斯算法：它不会得到不正确的解。一旦用拉斯维加斯算法找到一个解，这个解就一定是正确的解，但有时用拉斯维加斯算法找不到解。(可能给出问题的正确答案，也可能得不到问题的答案 )

4.舍伍德算法：它总能求得问题的一个解，且所求得的解总是正确的当一个确定性算法在最坏情况下的计算复杂性与其在平均情况下的计算复杂性有较大差别时，可在这个确定性算法中引入随机性将它改造成一个舍伍德算法，消除或减少问题的好坏实例间的这种差别。能消除算法最坏特性与平均特性之间的差别。

1. 在下列算法中有时找不到问题解的是（）B
   A、蒙特卡罗算法 B、拉斯维加斯算法 C、舍伍德算法 D、数值概率算法
2. 下列哪一种算法是随机化算法。（）D
   A、贪心算法 B、回溯法 C、动态规划算法 D、舍伍德算法
3. 舍伍德算法是（）B
   A、分支界限算法 B、随机化算法 C、贪心算法 D、回溯算法
4. 下列随机算法中运行时有时候成功有时候失败的是（）C
   A、数值概率算法 B、舍伍德算法 C、拉斯维加斯算法 D、蒙特卡罗算法
5. 下列哪一种算法不是随机化算法（）C
   A、蒙特卡罗算法 B、拉斯维加斯算法 C、动态规划算法 D、舍伍德算法