实验六 基于 Dijsktra 算法的最短路径求解
发布时间:2024年01月18日
实验六 基于Dijsktra算法的最短路径求解
一、实验目的
1.掌握图的邻接矩阵表示法,掌握采用邻接矩阵表示法创建图的算法。
2.掌握求解最短路径的 Dijsktra 算法。
二、实验内容
一张地图包括 n 个城市,假设城市间有 m 条路径(有向图),每条路径的长度
已知。给定地图的一个起点城市和终点城市,利用 Dijsktra 算法求出起点到终
点之间的最短路径
三、实验实习设备及开发环境
Visual studio 2022
四.实验实习过程步骤(注意是主要关键步骤,不是所有步骤,适当文字+截图说明)
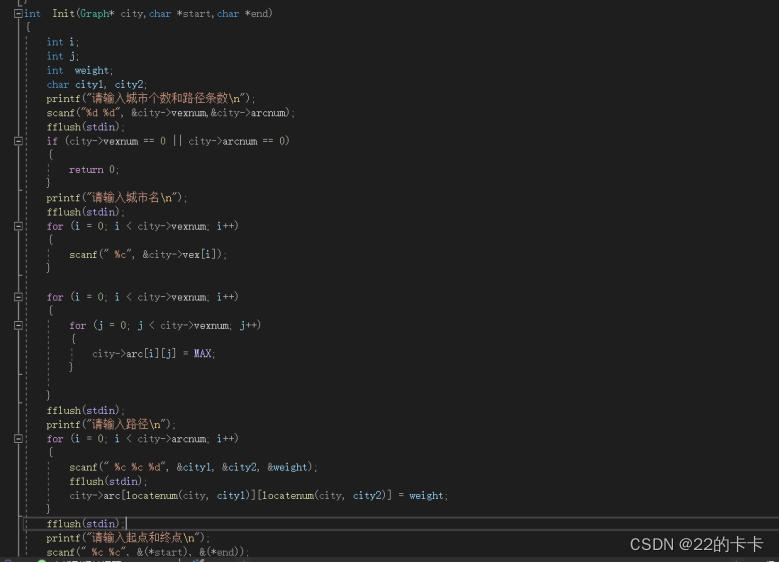
Function1:初始化图,将结构体里面的节点数和边数都输入,然后根据路径间的关系,对邻接矩阵进行填充,如果在两个节点间有路径,则在对应的邻接矩阵中修改权重(首先要将邻接矩阵初始化,就是将所有的全部变成无穷大)。因为题目中是有向图,所以不需要将对称的节点也修改,如果是无向图,就需要将对称的也修改。
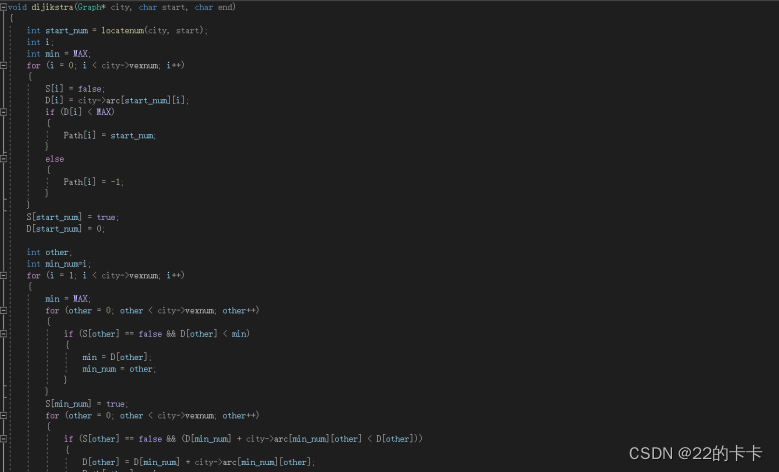
Funtion2:Dijkstra算法。从起点开始,建立一个数组来存储节点是否访问,一个数据记录节点离各点的距离,还有一个来记录最短路径。首先,从起点开始,将起点下标加入到最短路径数组里面,到个点距离首先设置为0,变为已经访问。然后依次访问有路径的节点,选择路径最小的节点,然后对这个节点,进行看看,是否加了这个节点后,这个节点到其他节点的路径是否变短了,如果有那么就更新路径。然后一直重复,直到访问完所有的节点。

五.实验实习结果及分析



实验结果成功。
六.实验遇到的问题及解决办法,实验心得体会及对此实验的意见或建议(有就写,无可不写)。
#include <stdio.h>
#include <stdlib.h>
#define MAX 99999
#define MAXVEX 100
#define true 1
#define false 0
int Path[MAXVEX];
int S[MAXVEX];
int D[MAXVEX];
typedef char Vexstype;
typedef int Arctype;
typedef struct Graph
{
Vexstype vex[MAXVEX];//顶点
Arctype arc[MAXVEX][MAXVEX];//邻接矩阵
int vexnum, arcnum;//顶点和边数
}Graph;
int locatenum(Graph* city, char citynum)
{
int i;
for (i = 0; i < city->vexnum; i++)
{
if (citynum == city->vex[i])
{
return i;
}
}
}
int Init(Graph* city,char *start,char *end)
{
int i;
int j;
int weight;
char city1, city2;
printf("请输入城市个数和路径条数\n");
scanf("%d %d", &city->vexnum,&city->arcnum);
fflush(stdin);
if (city->vexnum == 0 || city->arcnum == 0)
{
return 0;
}
printf("请输入城市名\n");
fflush(stdin);
for (i = 0; i < city->vexnum; i++)
{
scanf(" %c", &city->vex[i]);
}
for (i = 0; i < city->vexnum; i++)
{
for (j = 0; j < city->vexnum; j++)
{
city->arc[i][j] = MAX;
}
}
fflush(stdin);
printf("请输入路径\n");
for (i = 0; i < city->arcnum; i++)
{
scanf(" %c %c %d", &city1, &city2, &weight);
fflush(stdin);
city->arc[locatenum(city, city1)][locatenum(city, city2)] = weight;
}
fflush(stdin);
printf("请输入起点和终点\n");
scanf(" %c %c", &(*start), &(*end));
return 1;
}
void dijikstra(Graph* city, char start, char end)
{
int start_num = locatenum(city, start);
int i;
int min = MAX;
for (i = 0; i < city->vexnum; i++)
{
S[i] = false;
D[i] = city->arc[start_num][i];
if (D[i] < MAX)
{
Path[i] = start_num;
}
else
{
Path[i] = -1;
}
}
S[start_num] = true;
D[start_num] = 0;
int other;
int min_num=i;
for (i = 1; i < city->vexnum; i++)
{
min = MAX;
for (other = 0; other < city->vexnum; other++)
{
if (S[other] == false && D[other] < min)
{
min = D[other];
min_num = other;
}
}
S[min_num] = true;
for (other = 0; other < city->vexnum; other++)
{
if (S[other] == false && (D[min_num] + city->arc[min_num][other] < D[other]))
{
D[other] = D[min_num] + city->arc[min_num][other];
Path[other] = min_num;
}
}
}
}
void printPath(Graph* city, int end_num)
{
if (Path[end_num] != -1)
{
printPath(city, Path[end_num]);
}
printf("%c ", city->vex[end_num]);
}
void findend(Graph* city, char end)
{
int end_num = locatenum(city, end);
printf("最短长度为%d\n", D[end_num]);
int i;
fflush(stdin);
printf("最短路径为\n");
printPath(city, end_num);
printf("\n");
}
int main()
{
Graph city;
int vexnum, arcnum;
char start, end;
while (Init(&city,&start,&end))
{
dijikstra(&city, start, end);
findend(&city, end);
}
return 0;
}
文章来源:https://blog.csdn.net/m0_73605862/article/details/135649011
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
最新文章
- Python教程
- 深入理解 MySQL 中的 HAVING 关键字和聚合函数
- Qt之QChar编码(1)
- MyBatis入门基础篇
- 用Python脚本实现FFmpeg批量转换
- 力扣题:数字与字符串间转换-12.22
- 原生Android项目中引入Flutter并实现android 与 flutter 之间的通信
- 1901年-2022年全球气象数据CRU TS下载
- 深入理解Mysql事务隔离级别与锁机制
- 各地加速“双碳”落地,数字能源供应商怎么选?
- Django 构建动态前端页面详解
- 力扣(leetcode)第415题字符串相加(Python)
- Linux命令-ab命令(Apache服务器的性能测试工具 )
- 今天谈谈栈和队列的区别?
- MFC连接mqtt服务器订阅和发送数据-自设计函数库