Local Binary Convolutional Neural Networks （LBCNN）

论文：https://arxiv.org/abs/1608.06049

代码：GitHub - juefeix/lbcnn.torch: Torch implementation of CVPR'17 - Local Binary Convolutional Neural Networks http://xujuefei.com/lbcnn.html

摘要：

我们提出了局部二值卷积(LBC)，这是标准卷积神经网络(CNN)中卷积层的有效替代方案。LBC的设计原则是由局部二进制模式(LBP)驱动的。LBC层由一组固定的稀疏预定义的在训练过程中不更新的二元卷积滤波器、一个非线性激活函数和一组可学习的线性权值组成。线性权重结合激活滤波器响应来近似标准卷积层的相应激活滤波器响应。LBC层提供了显著的参数节省，与标准卷积层相比，可学习参数的数量减少了9到169倍。此外，与标准卷积层相比，权重的稀疏性和二值性也使模型大小节省了9到169倍。我们从理论上和实验上证明了我们的局部二进制卷积层是一个很好的近似标准卷积层。根据经验，具有LBC层的cnn，称为局部二进制卷积神经网络(LBCNN)，在一系列视觉数据集(MNIST, SVHN, CIF AR-10和ImageNet)上实现了与常规cnn相同的性能，同时节省了大量的计算量。

1. Introduction

深度学习在广泛的应用中取得了压倒性的成功，例如计算机视觉、语音识别/自然语言处理、机器翻译、生物医学数据分析等等。特别是深度卷积神经网络(CNN)，在过去几年中在解决许多计算机视觉问题方面取得了巨大的成功，这要归功于许多有效架构的巨大发展，AlexNet [21]， VGG[30]，盗梦空间[33]和ResNet[12,13]等等。然而，用完全可学习的卷积核对这些网络进行端到端训练(作为标准实践)是:(1)计算成本非常高，(2)在内存使用和磁盘空间方面导致模型尺寸大，以及(3)由于参数数量多，在有限的数据下容易过度拟合。

另一方面，越来越需要在资源受限的平台上部署这些系统，包括学习和推理，如自动驾驶汽车、机器人、智能手机、智能相机、智能可穿戴设备等。为了解决这些缺点，已经提出了几种二进制版本的cnn[6,5,28]，它们用二进制权值近似密集实值权值。通过有效的二进制卷积实现，二进制权重节省了大量的计算量。然而，与实值网络权重相比，cnn的完全二值化会导致性能损失。

在本文中，我们提出了一种替代方法来降低cnn的计算复杂性，同时执行标准cnn。我们引入了近似于标准卷积层的非线性激活响应的局部二值卷积(LBC)层。LBC层包括固定的稀疏二值滤波器(称为锚值权重)、非线性激活函数和一组可学习的线性权重(用于计算激活的卷积响应映射的加权组合)。学习简化为优化线性权重，而不是优化卷积滤波器。在学习阶段，根据卷积滤波器的空间维度(分别为3 × 3到13 × 13大小的滤波器)，以及由于二进制滤波器的稀疏特性而节省的计算和内存，可以实现至少9×到169×的参数节省。具有LBC层的cnn，称为局部二进制卷积神经网络(LBCNN)1，具有更低的模型复杂性，因此不容易过度拟合，非常适合资源受限环境下cnn的学习和推理。

我们的理论分析表明，LBC层是标准卷积层非线性激活的良好近似。我们还通过经验证明，具有LBC层的cnn在一系列视觉数据集(MNIST, SVHN, CIFAR-10和ImageNet)上的表现与常规cnn相当，同时在训练期间的参数数量方面显着节省。与密集可学习的实值滤波器相比，由于我们的二值滤波器的稀疏和预定义性质，计算和内存需求更大。

Related Work:

对卷积层使用二值滤波器的想法并不新鲜。BinaryConnect[6]被提出用二值权来近似神经网络中的实值权。给定任何实值权值，它随机分配+1的概率为p，该概率取自实值权值的硬s型输出，并且随机分配- 1的概率为1 - p。权重仅在前向和后向传播过程中二值化，而在参数更新步骤中则不进行二值化，在参数更新步骤中，更新权重需要高精度的实值权重。因此，在网络训练过程中，BinaryConnect在二值化权值和实值权值之间交替使用。在BinaryConnect[6]的基础上，提出了二值化神经网络(binalized neural network, BNN)[5]和量化神经网络(quantized neural network, QNN)[14]，其中权重和激活都被约束为二值。这些方法通过将大多数32位浮点乘法累积替换为1位xnor计数操作，大大提高了运行时效率。

BinaryConnect和BNN都证明了二进制网络在MNIST、CIFAR-10和SVHN数据集上的有效性。最近，XNOR-Net[28]基于BNN的设计原则，提出了一种可扩展的方法来学习用于大规模图像识别任务的二值化网络，并在ImageNet分类任务上展示了高性能。上述所有方法都在权重更新过程中使用高精度实值权重，并使用XNOR位计数实现高效。

XNOR-Net与BNN的区别在于二值化方法和网络架构。除了网络二值化，模型压缩和网络量化技术[15,35,10,2,7,11,31,8]是另一类试图解决cnn计算限制的技术。

然而，这些方法的性能通常受到未压缩和未量化模型的上限。我们提出的LBCNN与完全二值化的神经网络明显不同，并从局部二值模式中获得灵感。LBCNN具有固定和可学习权重的混合组合，提供了一种完全可学习卷积层的替代公式。通过只考虑固定权值的稀疏权值和二值权值，LBCNN还能够利用稀疏性和权值二值化所提供的所有统计和计算效率。

我们从理论上和经验上证明，LBCNN是一个非常好的近似标准可学习卷积层。

2. Forming LBP with Convolutional Filters

局部二值模式(LBP)是一个简单但非常强大的手工设计的图像描述符根植于人脸识别社区。LBP已被广泛采用在许多其他计算机视觉、模式识别和图像处理应用[27]。

传统的LBP算子[18,25,19,17]对大小为3 × 3、5 × 5等的图像块进行运算。LBP描述符是通过将相邻像素的强度与patch内中心像素的强度进行顺序比较而形成的。与中心像素相比，具有较高强度值的相邻像素被赋值为1和0。

最后，依次读取这个位串，并将其映射为一个十进制数(以2为基数)，作为分配给中心像素的特征值。这些聚合特征值表征了图像中的局部纹理。patch内中心像元(xc, yc)的LBP可以表示为LBP(xc, yc) = PL?1 n=0 s(in, ic)·2n，其中in表示第n个相邻像元的强度，ic表示中心像元的强度，L表示序列长度，≥ic时s(·)= 1，否则s(·)=0。例如，一个N × N的邻域由N 2?1个相邻像素组成，因此得到N 2?1个长位串。图1显示了大小为3 × 3和5 × 5的局部图像补丁的LBP编码示例。

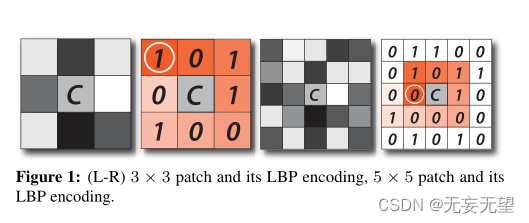
LBP公式的不同参数和配置可能导致截然不同的特征描述符。我们现在提出了一些变体，可以帮助推广基本的LBP描述符:

Base:

以2为基数通常用于对LBP描述符进行编码。因此，用于编码LBP位串的权重被限制为2的幂。放宽这些约束并允许权重取任意实值可以潜在地推广LBP描述符。

Pivot:

通常选择邻域的物理中心作为比较patch中像素强度的枢轴。在patch中选择不同的位置作为支点可以使LBP编码不同的局部纹理模式。此外，比较函数s(·)可以是多个枢轴的函数，从而对局部纹理进行更细粒度的编码。

Ordering:

LBP通过选择特定的像素顺序对patch的局部纹理进行编码，从而部分保留patch的空间信息。对于固定的邻域大小和枢轴，选择不同的邻域排序会导致对局部纹理的编码不同。

前面提到的所有变化，即枢轴、基底的选择，以及编码邻域的顺序，通常由经验决定，取决于应用。能够在一个可学习的框架中概括这些变化因素是LBCNN设计背后的动机和灵感之一，下面将讨论。

首先，让我们使用卷积滤波器更有效地重新表述LBP编码。传统的LBP特征编码实现使用一个3 × 3的窗口以重叠的方式扫描整个图像。在每个3 × 3的patch中，编码涉及(1)计算枢轴和相邻像素(或更一般的像素对)之间的差异，(2)将像素差异映射到二进制值的非线性阈值操作，以及(3)通过加权和将二进制值池化。

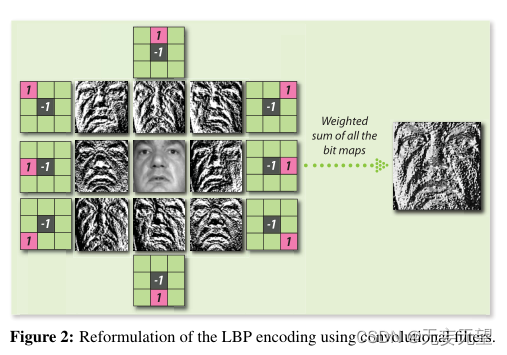
现在，用8个3 × 3卷积滤波器对整个图像进行简单的卷积，然后进行简单的二值化，就可以达到同样的目的，如图2所示。每个卷积滤波器都是一个2稀疏差分滤波器。二值化后的8个结果位映射也显示了出来。LBP的标准公式是使用预定义的权重向量v =[27,26,25,24,23,22,21,20]对所有位映射进行加权和。因此，标准的LBP特征提取可以重新表述为y =P8 i=1 σ(bi?x)·vi，其中x∈Rd是原始图像的矢量化版本，bi是稀疏卷积滤波器，σ是非线性二值化算子，在这种情况下是Heaviside步进函数，y∈Rd是得到的LBP图像。

通过适当地改变线性权重v，可以改变编码的基数和顺序。类似地，通过适当地改变卷积滤波器中的非零(+1和-1)支持，我们可以改变主轴。如上所述的LBP的重新表述构成了所提议的LBC层的基础。

3. LBCNN

3.1. Local Binary Convolution Module

令人惊讶的是，上述传统LBP描述符的重构具有卷积神经网络所需的所有主要成分。例如，在LBP中，图像首先由一组卷积滤波器过滤，然后通过Heaviside阶跃函数进行非线性操作。最后，将得到的位映射线性组合以获得最终的LBP符号，该符号可以作为下一层进一步处理的输入。?

这种LBP的替代观点激发了局部二进制卷积(LBC)层的设计，作为标准卷积层的替代方案。本文将LBC层的神经网络称为局部二值卷积神经网络(local binary convolutional neural networks, LBCNN)2。如图3所示，LBCNN的基本模块由m个预定义的固定卷积滤波器(锚权值)bi, i∈[m]组成。输入图像xl被这些LBC滤波器过滤，生成m个差分映射，然后通过非线性激活函数激活，产生m个位映射。

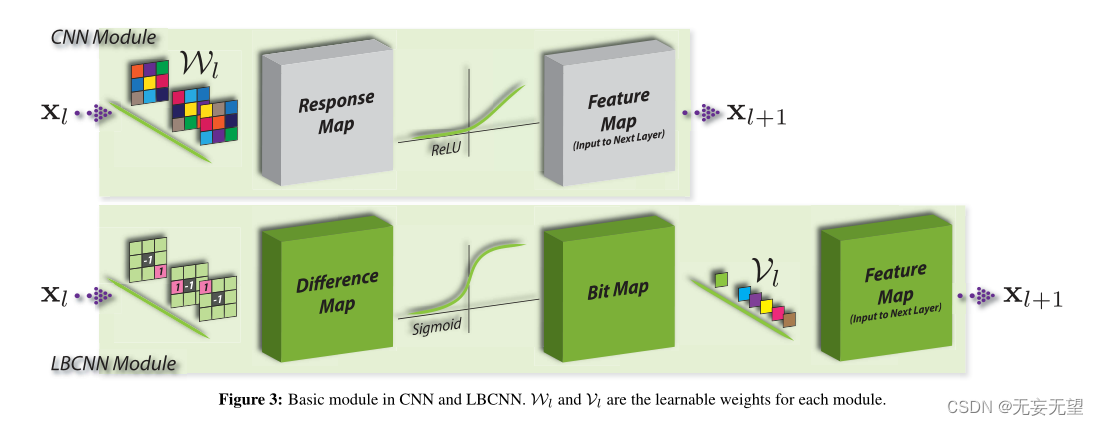
为了允许通过LBC层进行反向传播，我们将LBP中的不可微Heaviside阶跃函数替换为可微激活函数(sigmoid或ReLU)。最后，m位映射通过m个可学习的权重Vl,i, i∈[m]进行线性组合，生成最终LBC层响应的一个通道。LBC层的feature map作为下一层的输入xl+1。LBC层对广义多通道输入xl的响应可以表示为:

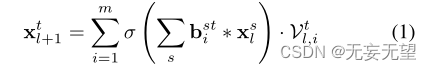
t是输出通道，s是输入通道。值得注意的是，计算激活的加权和的最后一步可以通过使用大小为1×1的过滤器的卷积操作来实现。因此，每个LBC层由两个卷积层组成，其中第一个卷积层的权值是固定的且不可学习的，而第二个卷积层的权值是可学习的。

在相同卷积核大小和输入输出通道数量的情况下，LBC层(1 × 1卷积)可学习参数的数量明显少于标准卷积层。设输入通道数为p，输出通道数为q。标准卷积层由p·h·w·q个可学习参数组成，卷积核的大小为h × w。对应的LBC层由p·h·w·m个固定权值和m·q个可学习参数(对应于1 × 1卷积)组成，其中m为LBC层中间通道的个数，本质上是LBC滤波器的个数。1×1卷积作用于固定滤波器的m个激活映射以生成q通道输出。CNN与LBC的参数个数之比为:

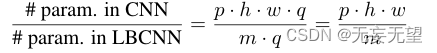
?为简单起见，假设p = m，将比值减小为h·w。因此，从数值上看，LBCNN在3 × 3、5× 5、7 × 7、9× 9、11 × 11和13 × 13卷积滤波器的学习过程中分别至少节省了9×、25×、49×、81×、121×和169×个参数。

3.2. Learning with LBC Layers

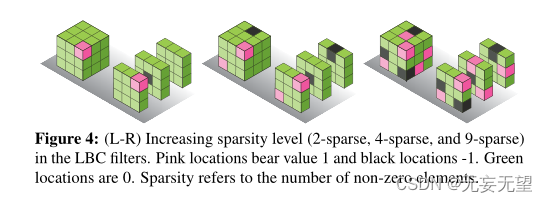
用LBC层而不是标准卷积层来训练端到端的网络是很简单的。梯度可以通过LBC层的锚权反向传播，就像它们可以通过可学习的线性权反向传播一样。这类似于在没有可学习参数的层中传播梯度(例如，ReLU, Max Pooling等)。然而，在学习过程中，只更新可学习的1 × 1滤波器，而锚点权重不受影响。在LBC中，大小为p × h × w × m的锚权(假设总共有m个中间通道)既可以确定地生成(就像在LBP中一样)，也可以随机生成。我们用后者来做实验。具体来说，我们首先确定一个稀疏度级别，即可以承受非零值的权重的百分比，然后以等概率(伯努利分布)随机分配1或-1给这些权重。该过程是传统LBP中权重的推广，因为我们允许将多个邻居与多个枢轴进行比较，类似于用于时空应用的3D LBP公式[27]。图4显示了随机过程为增加稀疏性级别(从左到右)而生成的权重的图形描述3。我们的随机LBC权值生成过程允许在每层使用更多样化的过滤器，同时对权值的稀疏性提供细粒度控制。

3.3. Theoretical Analysis （实在看不懂）

我们现在从理论上分析LBC层和标准卷积层之间的相似性，即近似质量，然后是ReLU非线性。给出了LBC层近似误差的上界。

在第1层，设x∈R(p·h·w)×1为来自p通道输入映射的矢量化的单个patch，其中h和w为卷积滤波器的空间大小。设w∈R(p·h·w)×1是卷积滤波器组w∈Rp×h×w×m中的一个矢量化的单卷积滤波器，在第1层有m个可学习的滤波器。为简洁起见，我们省略了层订阅l。

在标准CNN中，将该patch x投影到滤波器w上，然后进行非线性激活，得到输出特征值d。输出特征图的每个值都是输入映射x与卷积滤波器w卷积的直接结果。这个微观过程可以表示为:

所提出的LBC层对应的输出特征映射值是来自中间位映射的多个元素的线性组合(实现为1 × 1卷积)。通过将输入映射x与一组m个预定义的固定卷积滤波器B∈Rm×p×h×w进行卷积，然后进行非线性激活，得到该位图的每个切片。LBCNN对应的输出特征映射值d '是通过对m个中间位映射与q个参数为v1, v2，…的卷积滤波器22进行卷积线性组合得到的。， vmof大小为1 × 1。整个过程可以表示为:?

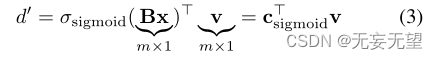
其中B现在是一个大小为m × (p·h·w)的二维矩阵，其中m个过滤器以行堆叠，稍微滥用了符号。

V = [v1，…]， vm]∈Rm×1。Eq. 2中的ReLU激活约束了输出的范围，即d≥0。情商。

3对输出值也有类似的约束，即由于sigmoid激活，csigmoid = σsigmoid(Bx)∈(0,1)。因此，我们总能得到这样一个v，即c = d ' = d。

然而，选择ReLU作为LBC的激活函数会诱导以下表达:

我们考虑两种情况(i) d = 0:由于crelu = σrelu(Bx)≥0，向量v∈Rm×1总是存在，使得d ' = d。然而，当(ii) d > 0时:很明显，当crelu = 0时，近似不成立。接下来，我们将展示crelu > 0以确保近似d '≈d成立的条件(定理3.5)。?

4. Experimental Results

我们将评估所提出的LBC层的有效性，并将其性能与几个数据集上的标准卷积层进行比较，包括小规模和大规模。

Datasets:

我们考虑在四个不同的视觉数据集上的分类任务，MNIST, SVHN, CIFAR-10和ILSVRC2012 ImageNet分类挑战。MNIST[22]数据集由60K的训练集和10K的32 × 32灰度0 ~ 9手写体数字图像的测试集组成。SVHN[24]也是一个广泛使用的数据集，用于对数字进行分类，在本例中是街景图像中的门牌号数字。它包括一个604K的训练集和一个26K的32 × 32彩色图像的测试集，显示门牌号数字。CIFAR-10[20]是一个图像分类数据集，包含一个50K的训练集和一个10K的32 × 32彩色图像的测试集，涵盖飞机、汽车、鸟、猫、鹿、狗、青蛙、马、船和卡车等10个类别。ImageNet ILSVRC-2012分类数据集[29]由1000个类组成，其中128万张用于训练，50K张用于验证。我们首先考虑这个数据集的一个子集。我们随机选择图像数量最多的100个类(每个类中有1300张训练图像，总共有130K张训练图像和5K张测试图像)，并在这个子集上报告top-1的准确率。完整的ImageNet实验结果也将在下一节中报告。

Implementation Details:?

从概念上讲，LBCNN可以在任何现有的深度学习框架中轻松实现。由于卷积权值是固定的，我们不需要计算梯度，也不需要更新权值。从计算的角度和内存的角度来看，这都可以节省。此外，由于权重是二进制的，卷积操作可以纯粹通过加法和减法来执行。我们将本文中评估的模型架构基于ResNet[13]，并使用默认的3 × 3过滤器大小。我们的基本模块是如图3所示的LBC模块以及ResNet中的身份连接。我们实验了不同数量的LBC单元，10,20和75，这相当于20,40和150个卷积层。对于LBCNN，卷积权值是按照3.2节中描述的过程生成的。我们使用512个随机生成的锚权重，稀疏度为0.1、0.5或0.9，用于我们所有的实验。卷积层后采用空间平均池化，将图像的空间维度降至6 × 6。我们使用学习率为1e-3，并采用[13]中的学习率衰减时间表。为了提高计算效率和更快的收敛速度，我们使用ReLU代替sigmoid作为非线性函数。

一个重要而实际的考虑是避免在LBC层之前使用ReLU激活。这是为了确保由于输入(由于ReLU激活)和卷积权重的稀疏性而没有不可恢复的信息丢失。

Baselines:

为了确保公平的比较，并量化我们的LBCNN方法和传统CNN之间的确切经验差异，我们对这两个网络使用了完全相同的架构，尽管是稀疏的，二进制和固定LBCNN的权值和CNN的密集可学习权值。在卷积滤波器的数量，初始学习率和学习率调度方面，我们也使用完全相同的数据和超参数。因此，在这些使用3 × 3卷积核的实验中，LBCNN的可学习参数减少了10倍(基线CNN还包括1 × 1卷积层)。

Results on MNIST, SVHN, and CIFAR-10:?

表1比较了在CIFAR-10数据集上LBCNN、具有共享卷积权值的LBCNN和具有规则卷积层的相应网络的准确率。注意，在卷积层数、输入输出通道数固定的情况下，网络的性能随着输出通道数q的增加而增加。值得注意的是，参数减少10倍的LBCNN的性能与相应的CNN一样好。

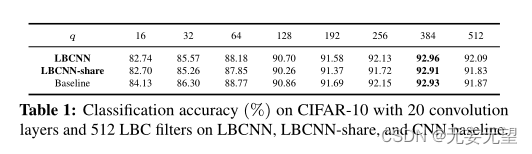
表2汇总了我们在不同数据集上的实验图像分类结果。将表现最好的lbcnn与其相应的CNN基线进行比较，并与最先进的方法(如BinaryConnect[6]、binalized Neural Networks (BNN)[5]、ResNet[12]、Maxout Network[9]、Network in Network (NIN)[23])进行比较。

5. Discussion

我们现在讨论了与常规卷积层相比，所提出的局部二进制卷积层所提供的一些计算和统计优势。

Computational:?

在训练和推理过程中，LBC层的参数化将可学习参数的数量减少了9倍至169倍。此外，卷积权重的稀疏性和二进制性进一步降低了训练和推理过程中的计算复杂性以及内存和空间需求。较低的内存要求可以学习更深层的神经网络，从而允许通过更深层的架构学习更好的表示[30,12,13]。此外，在所有LBC层之间共享卷积权值，可以进一步降低内存需求，从而使深度cnn能够在资源受限的嵌入式系统上学习。

Statistical:

与CNN相比，LBCNN模型更简单，可学习参数更少，可以有效地正则化学习过程，防止过拟合。高容量模型，如具有规则卷积层的深度cnn，通常由非常大量的参数组成。已经引入Dropout[32]、DropConnect[34]和Maxout[9]等方法，在训练过程中对网络的全连接层进行正则化，以避免过拟合。与正则化网络的全连接层[32,34,4]不同，LBCNN直接正则化卷积层，这在[32,3]中也很重要。

网络正则化技术，如Dropout[32]和Batch Normalization[16]，可以防止神经元激活的共适应，减少内部协变量移位。最近，Cogswell等[4]提出了一种显式去相关并最小化隐藏激活的交叉协方差的方法，以提高性能并防止过拟合。它鼓励多样化或非冗余的表示。LBCNN自然地为激活提供去相关，因为卷积滤波器是随机生成的稀疏伯努利滤波器。图6 (R)显示了第4节中描述的CIFAR-10上性能最好的体系结构的前5层的LBCNN和CNN滤波器的归一化相关量(kΣk2F?kdiag(Σ)k22)/kΣk2F)。归一化相关性的值越小，对应于激活之间的去相关性越大。

Sample Complexity:

LBCNN较低的模型复杂度使其成为低样本复杂度学习的一个有吸引力的选择。为了证明LBCNN的统计效率，我们在CIFAR-10数据集的一个子集上进行了实验。训练子集在保持测试集完整的情况下，随机抽取每个类25%的图像(5000 × 0.25 = 1250)。我们为CNN和LBCNN选择了第4节中描述的CIFAR-10上性能最好的体系结构。如图7 (L1)所示的结果表明，LBCNN的训练速度更快，并且不容易对训练数据进行过拟合。为了提供一个扩展的评估，我们在有限的样本复杂度设置下对FRGC v2.0数据集[26]进行了额外的人脸识别实验。每个类的图像数量在6 - 132张之间，平均51.6张。虽然总共有466个职业，但我们以60-40的训练/测试分割来增加随机选择的职业数量(10,50和100)。在类的数量上，我们的网络参数保持不变，除了最后的分类全连接层。我们从我们的研究结果中得出了一些观察结果(见图7 (R3)):(1) LBCNN比CNN收敛得更快，特别是在小数据集上;(2)LBCNN在这个任务上优于CNN。较低的模型复杂性有助于LBCNN防止过度拟合，特别是在中小型数据集上。

6. Conclusions

基于传统的局部二值模式，本文提出了局部二值卷积(local binary convolution, LBC)层作为标准CNN中卷积层的替代方案。

LBC层由一组稀疏的、二进制的、随机生成的固定卷积权值和一组可学习的线性权值组成。我们在理论上和经验上都证明了LBC模块是标准卷积层的良好近似值，同时也导致在训练中需要学习的参数数量显著减少，对于3 × 3和13 × 13大小的滤波器分别为9×到169×。具有LBC层的cnn由于其较低的模型复杂度和计算复杂度，非常适合于资源受限环境下深度cnn的低样本复杂度学习。本文提出的LBCNN在不同网络架构的多个小型和大型数据集上表现优异，性能与标准cnn相当。

参考：Local Binary Convolutional Neural Networks ---卷积深度网络移植到嵌入式设备上？ - 刘岩-- - 博客园