C#，最小生成树（MST）博鲁夫卡（Boruvka）算法的源代码

?Otakar Boruvka

本文给出Boruvka算法的C#实现源代码。

Boruvka算法用于查找边加权图的最小生成树（MST），它早于Prim和Kruskal的算法，但仍然可以被认为是两者的关联。

一、Boruvka算法的历史

1926年，奥塔卡·博鲁夫卡（Otakar Boruvka）首次提出了一种求给定图的MST的方法。这在计算机出现之前就已经存在了，事实上，它被用来设计一个高效的配电系统。

Georges Sollin在1965年重新发现了它，并将其用于并行计算。

二、Boruvka算法的思路

该算法的核心思想是从一组树开始，每个顶点代表一棵孤立的树。然后，我们需要不断增加边，以减少孤立树的数量，直到我们有一个单一的连接树。
让我们通过一个示例图逐步了解这一点：

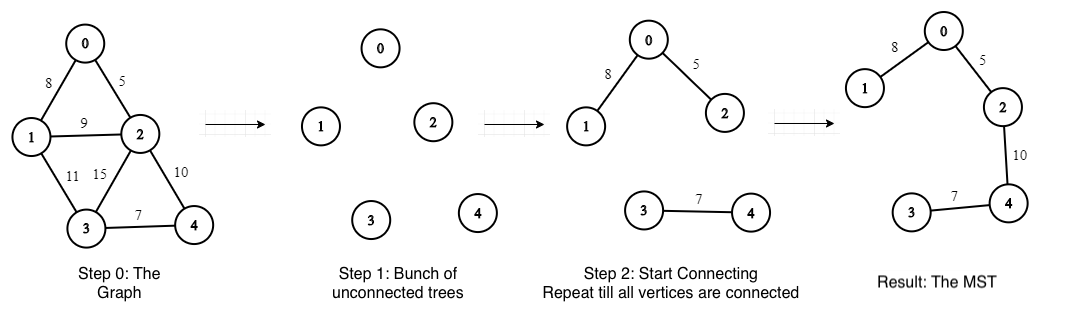
步骤0：创建一个图表；
步骤1：从一堆未连接的树开始（树的数量=顶点的数量）；
步骤2：当存在未连接的树时，对于每个未连接的树：
(1)以较小的重量找到它的边缘
(2)添加此边以连接另一棵树

三、Boruvka算法的源代码

1、核心代码

using System;
using System.Collections;
using System.Collections.Generic;

namespace Legalsoft.Truffer.Algorithm
{
    /// <summary>
    /// 图的连接边信息
    /// </summary>
    public class EdgeInfo
    {
        /// <summary>
        /// 起始节点编码（按一般教材习惯，1起步）
        /// </summary>
        public int Start { get; set; } = 0;
        /// <summary>
        /// 终点编码（按一般教材习惯，也从1起步）
        /// </summary>
        public int End { get; set; } = 0;
        /// <summary>
        /// 边的权值
        /// </summary>
        public int Weight { get; set; } = 0;
        /// <summary>
        /// 构造函数
        /// </summary>
        /// <param name="a"></param>
        /// <param name="b"></param>
        /// <param name="c"></param>
        public EdgeInfo(int a, int b, int c)
        {
            this.Start = a;
            this.End = b;
            this.Weight = c;
        }
    }

    /// <summary>
    /// MST-Boruvka算法
    /// </summary>
    public static class Boruvka_Minium_Spaning_Tree
    {
        private static int[] Parent { get; set; } = null;
        private static int[] Minium { get; set; } = null;

        /// <summary>
        /// 计算最小生成树（MST）的最小代价及树信息
        /// </summary>
        /// <param name="graph">图信息（边列表）</param>
        /// <param name="tree">返回树信息（边的列表）</param>
        /// <returns></returns>
        public static int Execute(EdgeInfo[] graph, out List<int> tree)
        {
            tree = new List<int>();

            // 计算最大节点编号
            int N = 0;
            for (int i = 0; i < graph.Length; i++)
            {
                if (graph[i].Start > N) N = graph[i].Start;
                if (graph[i].End > N) N = graph[i].End;
            }

            Parent = new int[N + 1];
            for (int i = 1; i <= N; i++)
            {
                Parent[i] = i;
            }
            Minium = new int[N + 1];

            int result = 0;
            int components = N;
            while (components > 1)
            {
                for (int i = 1; i <= N; i++)
                {
                    Minium[i] = -1;
                }

                for (int i = 0; i < graph.Length; i++)
                {
                    if (Root(graph[i].Start) == Root(graph[i].End))
                    {
                        continue;
                    }

                    int r_v = Root(graph[i].Start);
                    if (Minium[r_v] == -1 || graph[i].Weight < graph[Minium[r_v]].Weight)
                    {
                        Minium[r_v] = i;
                    }

                    int r_u = Root(graph[i].End);
                    if (Minium[r_u] == -1 || graph[i].Weight < graph[Minium[r_u]].Weight)
                    {
                        Minium[r_u] = i;
                    }
                }

                for (int i = 1; i <= N; i++)
                {
                    if (Minium[i] != -1)
                    {
                        if (Merge(graph[Minium[i]].Start, graph[Minium[i]].End))
                        {
                            result += graph[Minium[i]].Weight;
                            tree.Add(Minium[i]);
                            components--;
                        }
                    }
                }
            }

            return result;
        }

        private static int Root(int v)
        {
            if (Parent[v] == v)
            {
                return v;
            }
            return Parent[v] = Root(Parent[v]);
        }

        private static bool Merge(int v, int u)
        {
            v = Root(v);
            u = Root(u);
            if (v == u)
            {
                return false;
            }
            Parent[v] = u;
            return true;
        }
    }
}

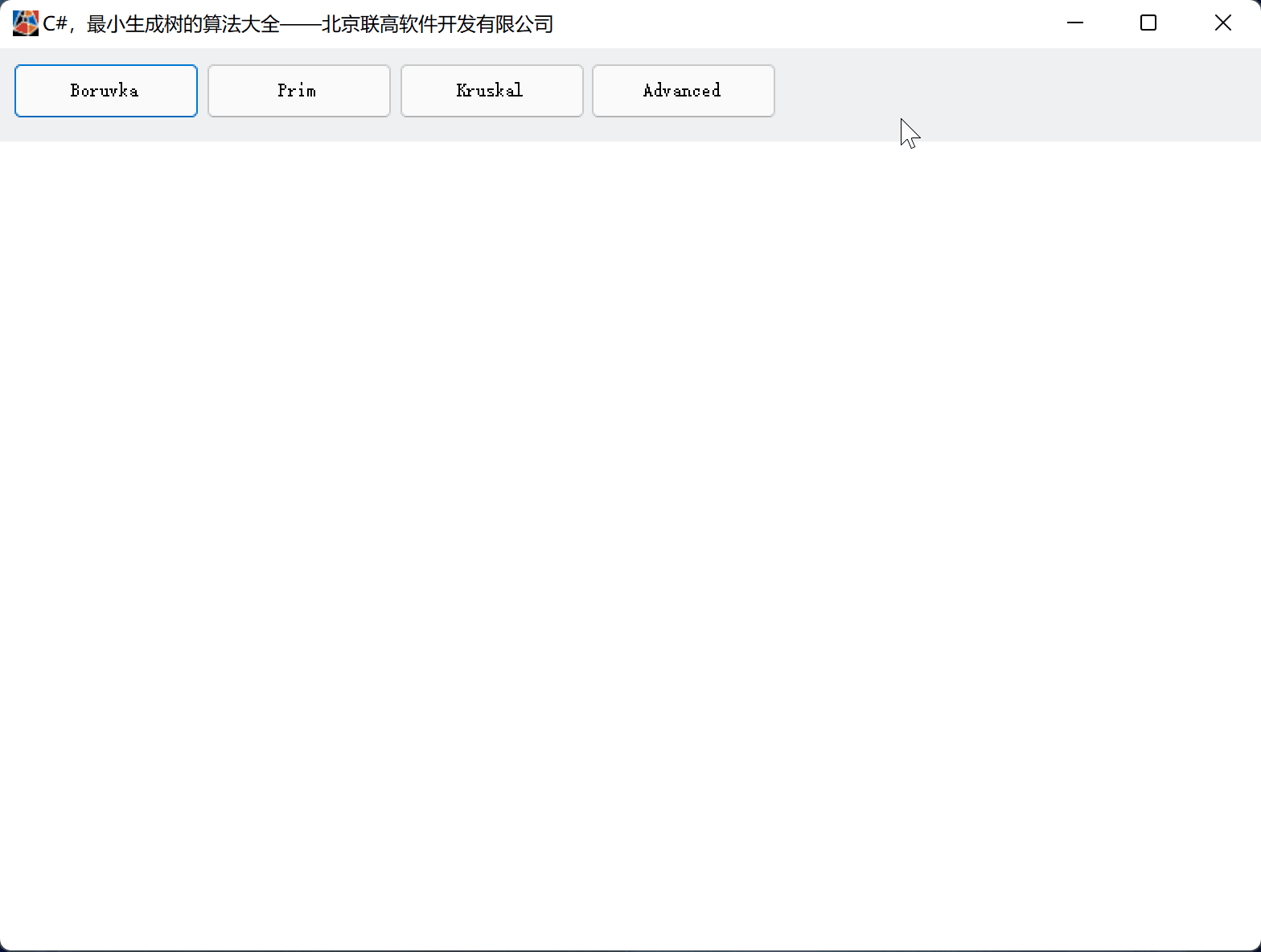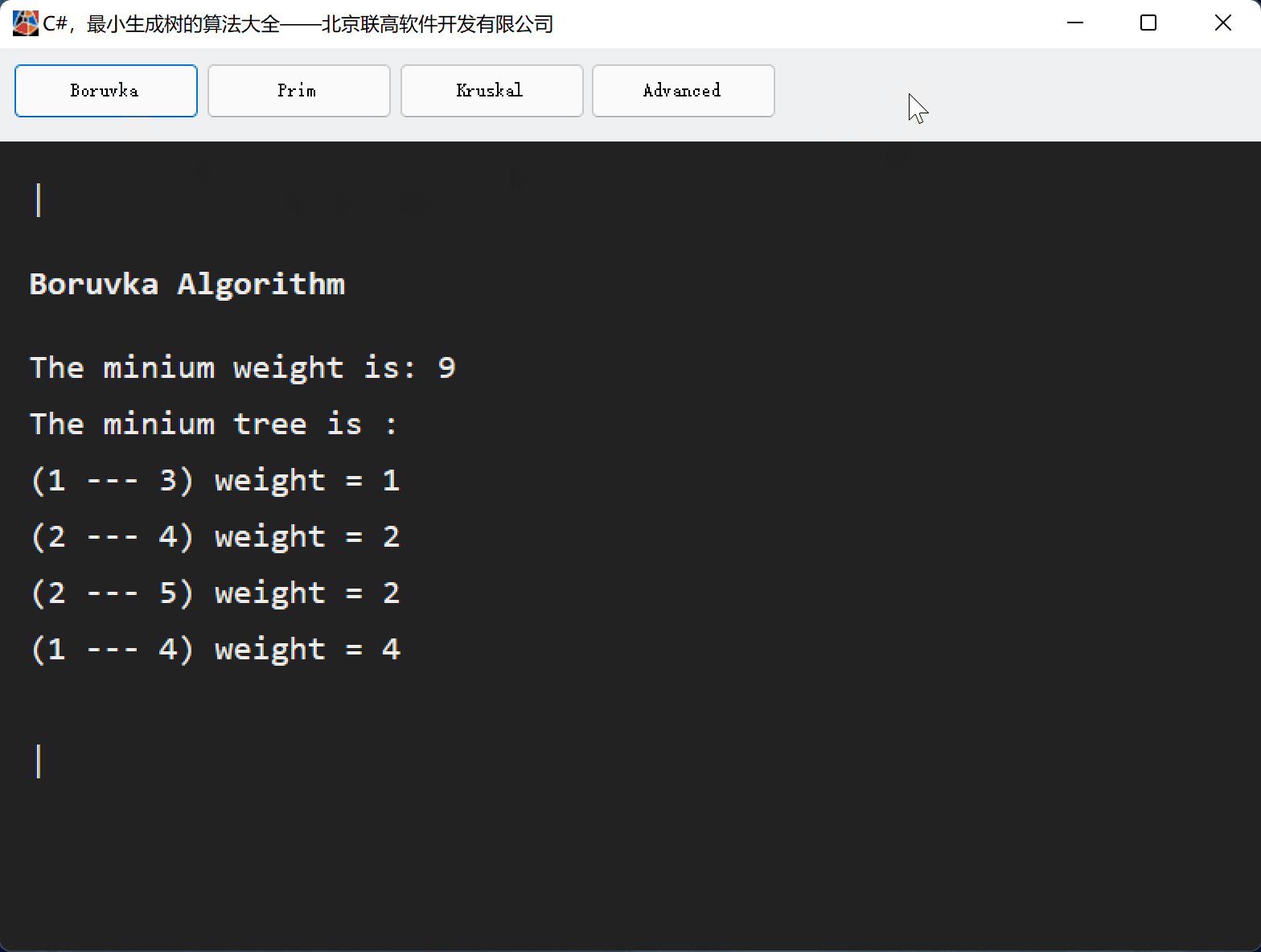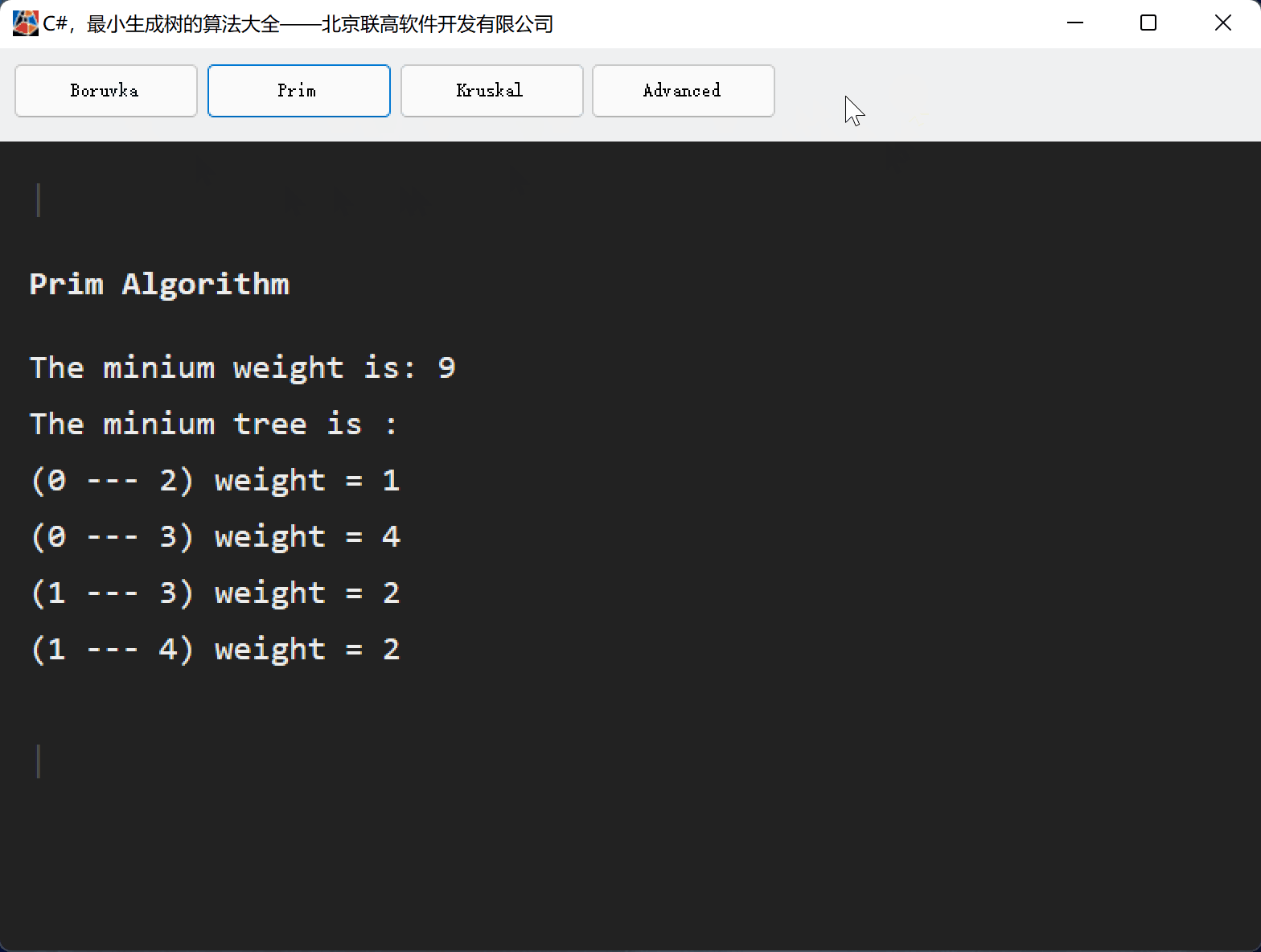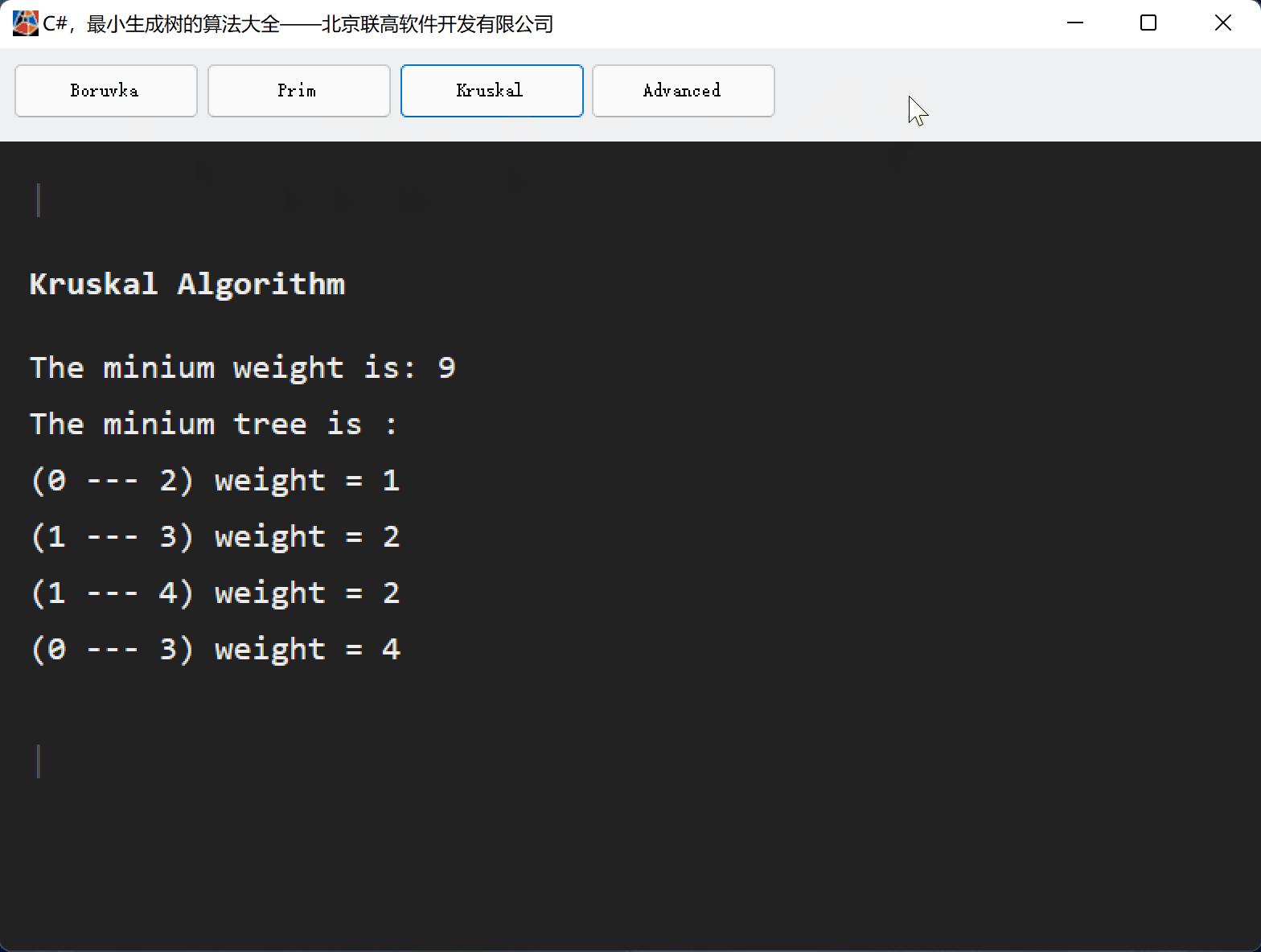
2、测试与显示

List<EdgeInfo> g = new List<EdgeInfo>();
g.Add(new EdgeInfo(1, 2, 6));
g.Add(new EdgeInfo(1, 3, 1));
g.Add(new EdgeInfo(1, 4, 4));
g.Add(new EdgeInfo(1, 5, 4));
g.Add(new EdgeInfo(2, 4, 2));
g.Add(new EdgeInfo(2, 5, 2));
g.Add(new EdgeInfo(3, 4, 8));

int weight = Boruvka_Minium_Spaning_Tree.Execute(g.ToArray(), out List<int> path);
StringBuilder sb = new StringBuilder();
sb.AppendLine("The minium weight is: " + weight + "<br>");
sb.AppendLine("The minium tree is : <br>");
foreach (int idx in path)
{
	sb.AppendLine("("+g[idx].Start + " --- " + g[idx].End + ") weight = " + g[idx].Weight + "<br>");
}
webBrowser1.DocumentText = sb.ToString();

更多算法源代码将陆续发布，建议关注。

——————————————————————————————————————————

POWER BY TRUFFER.CN