基础数论之组合与排列【C++算法竞赛】

为天梯赛备课？

????????先占个坑……说实话我最近的论文代码，也是因为排列组合数这个问题，导致速度不太能上去……顺便看看重新学一下能不能给我自己优化一下。

? ? ? ? 1.10就要讲课了！【咆哮--】还得给他们留几个练习题，我还得写题解o(TヘTo)

? ? ? ? 组合数与排列的题目中，有很多是提高题，难度较大，在本章节仅提供基础数学知识，与较为简单的题目，和万能模板。

组合数

数学概念及公式

????????组合数公式是指从 n 个不同元素中，任取 m(m≤n) 个元素并成一组，叫做从 n 个不同元素中取出 m 个元素的一个组合。

????????从 n 个不同元素中取出 m(m≤n) 个元素的所有组合的个数，叫做 n 个不同元素中取出 m 个元素的组合数。用符号 C(n,m) 表示。

? ? ? ?组合数公式如下：

组合数的性质

下面分享计算组合数的数学公式，作为知识补充。

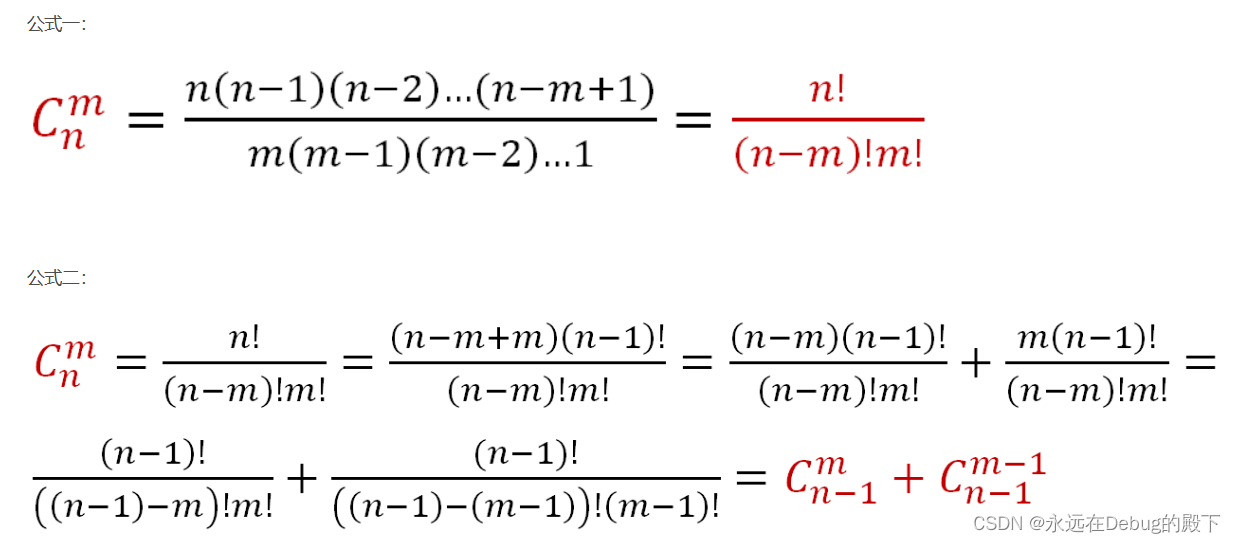
? ? ? ? 上图是对组合数基础性质的证明，在这里不过多叙述理论组成。

组合数的计算

根据定义（根据公式一）

????????根据上面的公式1，可以进行计算，下面的代码就是公式一的具象体现。但是其时间复杂度较高，大概需要n！

long long C(long long n, long long m) 
{
    long long ans = 1;
    for (long long i = 1; i <= n; i++) 
    {
        ans *= i;

    }
    for (long long i = 1; i <= m; i++) 
    {
        ans /= i;
    }
    for (long long i = 1; i <= n - m; i++) 
    {
        ans /= i;
    }
    return ans;
}

????????如果面对数值较大的情况，运算速度肯定会被卡，这样的话就需要一定的优化，优化一般分为两个部分，一个是在数学公式上的优化，或者是总结规律减少循环次数，咱们先重点看下组合数的变形公式

变式（根据公式二）

? ? ? ? 直接一个套娃

? ? ? ? 我们使用递归的方法，套用公式：

long long C2(long long n, long long m) 
{
    if (m == 0 || m == n) return 1;
    return C(n - 1, m) + C(n - 1, m - 1);
}

? ? ? ? 这样的速度相对来说会快一点，减少了很多循环运算

????????最后还有一种被称为？边乘边除的方法？

????????我没有试过他的时间复杂度，仅做一下分享

long long C3(long long n, long long m) 
{
    long long ans = 1;
    for (long long i = 1; i <= m; i++) {
        ans = ans * (n - m + i) / i; 
    }
    return ans;
}

与排列数互通

????????此处留在排列数部分讲解

完整代码

#include<stdio.h>
#include<iostream>
#include<string.h>
using namespace std;


long long C(long long n, long long m) 
{
    long long ans = 1;
    for (long long i = 1; i <= n; i++) 
    {
        ans *= i;

    }
    for (long long i = 1; i <= m; i++) 
    {
        ans /= i;
    }
    for (long long i = 1; i <= n - m; i++) 
    {
        ans /= i;
    }
    return ans;
}

long long C2(long long n, long long m) 
{
    if (m == 0 || m == n) return 1;
    return C(n - 1, m) + C(n - 1, m - 1);
}

long long C3(long long n, long long m) 
{
    long long ans = 1;
    for (long long i = 1; i <= m; i++) {
        ans = ans * (n - m + i) / i; 
    }
    return ans;
}

int main()
{
   long long n, m;
    cin >> n >> m;
    long long sum = C3(n, m);
    cout << sum;
    return 0;
}

组合的输出

? ? ? ? 这是一种很基础的模板题型，一般都是用枚举的方法，我们之间上一个例题讲解一下

例题

Description
排列与组合是常用的数学方法，其中组合就是从n个元素中抽出r个元素(不分顺序且r<＝n)，我们可以简单地将n个元素理解为自然数1，2，…，n，从中任取r个数。
现要求你用递归的方法输出所有组合。

Input
一行两个自然数n、r(1<n<21，1<＝r<＝n)。

Output
所有的组合，每一个组合占一行且其中的元素按由小到大的顺序排列，每个元素占三个字符的位置，所有的组合也按字典顺
序。

Sample Input
5 3

Sample Output
1 2 3
1 2 4
1 2 5
1 3 4
1 3 5
1 4 5
2 3 4
2 3 5
2 4 5
3 4 5

解析

? ? ? ? 打表肯定是可以的，虽说这个数值范围适中，方式代码行数依然很多，如果说实在没有思路，为了AC那打表就打表吧，但是真的在比赛的时候，时间也很重要（当然AC更重要），总之打表比较浪费时间，可以用递归＋枚举/回溯与深搜/STL库

????????先谈C++的一大特点 STL库，在上节课已经初步介绍了STL库，其中有很多非常实用的函数，一部分最基础的，需要大家熟悉记忆，另外一部分则是在做题的过程中，边练边学。

? ? ? ? 在本题中，先引入头文件#include<algorithm>，其中有全排列函数，next_permutation()，

next_permutation()

? ? ? ? 简单介绍一下全排列的用法，计算序列全排列的函数：next_permutation（start,end），和prev_permutation（start,end）。这两个函数作用是一样的，区别就在于前者求的是当前排列的下一个排列，后一个求的是当前排列的上一个排列。至于这里的“前一个”和“后一个”，我们可以把它理解为序列的字典序的前后。

? ? ? ? 在这里咱们重点看一下next_permutation（）

????????对于next_permutation函数，其函数原型为

     #include <algorithm>

     bool next_permutation(iterator start,iterator end)

????????当 当前序列不存在下一个排列时，函数返回false，否则返回true

? ? ? ? 本题中，x[i]代表第i选或不选，0代表选，1代表不选

#include<iostream>
#include<algorithm>
#include<iomanip>
int x[30];
using namespace std;
int main() 
{
    int n, r;
    cin >> n >> r;
    for (int i = r + 1; i <= n; ++i)
        x[i] = 1; 
    do {
        for (int i = 1; i <= n; ++i)
            if (x[i] == 0) 
                cout << setw(3) << i;
        cout << endl;
    } while (next_permutation(x + 1, x + n + 1));
    return 0;
}

? dfs

? ? ? ? 或者使用DFS的方法

#include<iostream>
#include<iomanip>
using namespace std;
int r, a[100], n;
void dfs(int k) {//搜索第k个数
    int i;
    if (k > r) {
        for (i = 1; i <= r; i++) {
            cout << setw(3) << a[i];//输出，场宽为三
        }
        cout << endl;
        return;//回到前一层
    }
    for (i = a[k - 1] + 1; i <= n; i++) {
        a[k] = i;
        dfs(k + 1);//直接进行下一次调用
    }
}
int main()
{
    cin >> n >> r;
    dfs(1);
    return 0;
}

排列数

数学概念及公式

????????排列数公式就是从n个不同元素中，任取m（m≤n）个元素，按照一定的顺序排成一列。

? ? ? ? ！注意：排列与元素的顺序有关，组合与顺序无关。

排列数的性质

排列数具有两种不同的计算方法：

?排列数的计算

根据公式：

int A(int n, int m) 
{
	int res = 1;
	for (int i = m; i >= 1; i--) 
	{
		res *= n;	
		n--;
	}
	return res;
}

根据排列数求组合数

#include<iostream>
#include<iomanip>
#include<cmath>
using namespace std;
int A(int n, int m) 
{
	int res = 1;
	for (int i = m; i >= 1; i--) 
	{
		res *= n;	
		n--;
	}
	return res;
}
int C(int n, int m) 
{
	m = min(m, n - m);

	int numerator = A(n, m);	
	int denominator = A(m, m);	
	return numerator / denominator;
}

int main()
{
	int n, m;
    cin >> n >> m;
	cout << C(n, m) << endl;;
    return 0;
}

排列的输出

? ? ?这部分浅浅讲一下，主要是给后面DFS打一个基础，常规还是用搜索算法，后面讲DFS的时候会见到，这里就主要是以数论、数学概念为主。? ?

题目

题目描述
????????按照字典序输出自然数 1 到 n 所有不重复的排列，即 n 的全排列，要求所产生的任一数字序列中不允许出现重复的数字。
输入

3
输出

? ? 1 ? ?2 ? ?3
? ? 1 ? ?3 ? ?2
? ? 2 ? ?1 ? ?3
? ? 2 ? ?3 ? ?1
? ? 3 ? ?1 ? ?2
? ? 3 ? ?2 ? ?1
?

代码

?用的STL库函数 next_permutation()

#include<cstdio>
#include<iostream>
#include<algorithm>
using namespace std;
int x[11];
int main()
{
    int n;
    cin >> n;
    for (register int i = 1; i <= n; i++)
    {
        x[i] = i;
        cout << i<< ' ';
    }

    while (next_permutation(x + 1, x + 1 + n)) 
    { 
        cout << endl;
        for (register int i = 1; i <= n; i++)
            cout << x[i] << ' ';
    }
    return 0;
}

本章推荐习题：

（后面会发布题解的……在日程中，反正也是洛谷的题，肯定是公开题解的，貌似也不用催我TAT但是老师那里还需要我交一份题解给大一的啊啊啊啊啊啊啊）

? ? ? ? 同事推荐学有余力的同学，使用DFS解一下今天的例题

「EZEC-10」排列排序 - 洛谷

[NOIP2016 提高组] 组合数问题 - 洛谷