深度学习 | 梯度下降算法及其变体

发布时间：2023年12月23日

一、最优化与深度学习

1.1、训练误差与泛化误差

?????????

?1.2、经验风险

?????????

?1.3、优化中的挑战

?????????

?????? 1.3.1、局部最小值

????????

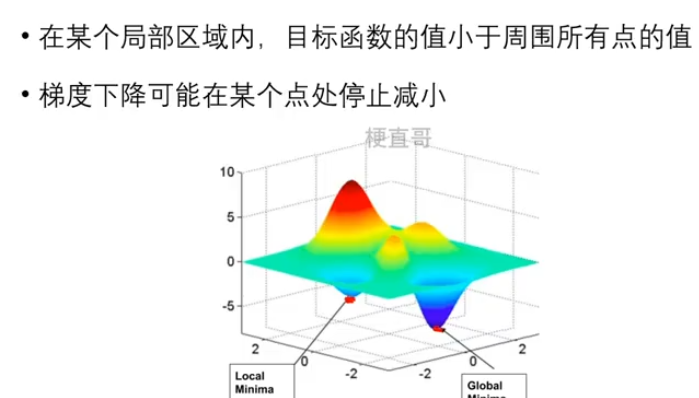
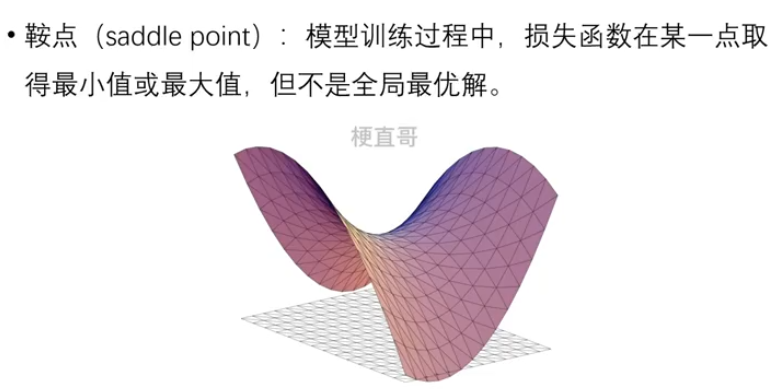
??????? 1.3.2、鞍点

????????经常是由于模型复杂度过高或者训练样本数据过少造成的 —— Overfitting

????????

??????? 1.3.3、悬崖

????????

???????? 1.3.4、长期依赖问题

????????

二、损失函数

2.1、损失函数的起源

损失函数(loss function)：衡量预测值和真实值之间差异的函数
损失函数的起源可以追溯到统计学和最小二乘法

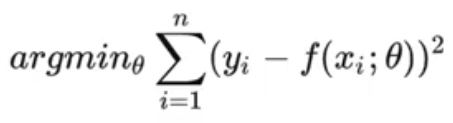
?2.2、基础

最大似然估计 Maximum Likelihood Estimation,MLE
- 假定X服从p model
- 若p（似然函数）为高斯分布，MLE即为最小化均方误差MSE
交叉嫡损失概率分布解释 Cross Entropy
- 交叉嫡损失从概率分布角度来说,也是最大似然估计MLE
- 若我们不知道p model或者他不是高斯分布，此时我们可以通过训练样本的出现概率来估计，相当于缩放了上面的函数，此公式即交叉熵损失的定义
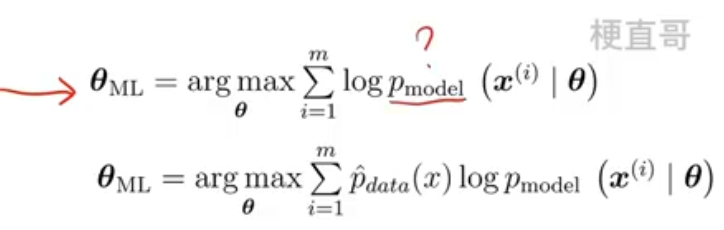
最大化后验 Maximum A Posteriori
- L2正则化 —— 先验为高斯分布
- L1正则化 —— 先验为拉普拉斯分布
贝叶斯估计 Bayesian Estimation
- 频率派的人认为数据是含有参数的随机变量
- 贝叶斯派认为数据是被直接观测到的，因此不是随机的

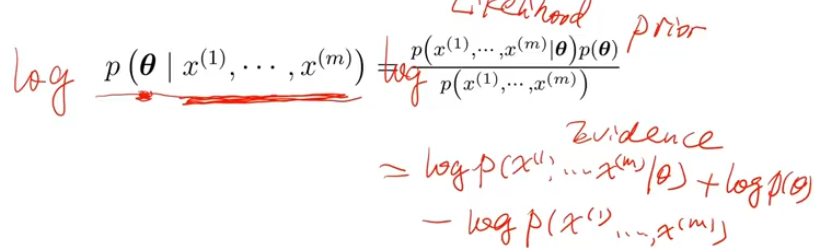
2.3、损失函数的性质

可微性(differentiability) ︰函数在任意一点处都有一个导数
可导性(continuity) ︰函数有连续的导函数
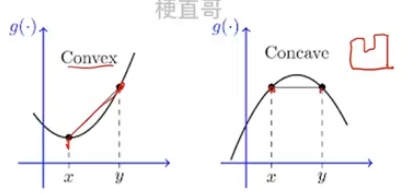
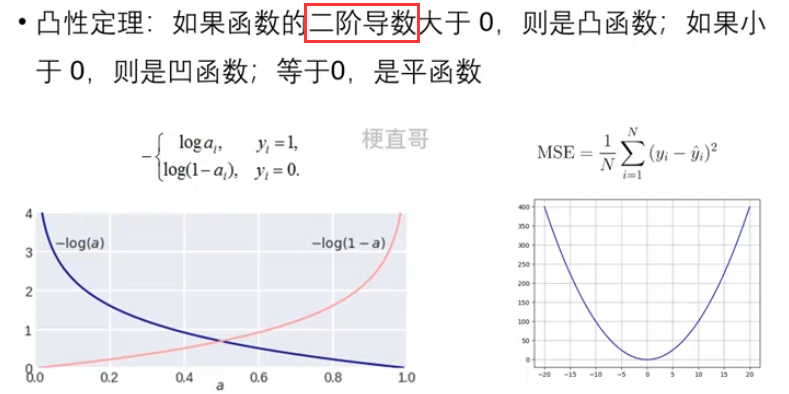
凸函数保证损失函数有全局最小值，可以用较简单优化算法
凹函数则需要使用更复杂的优化算法找最小值
如何判断函数凸性？
凸约束和凸优化
- 凸约束可以将非凸问题转化成凸优化问题。
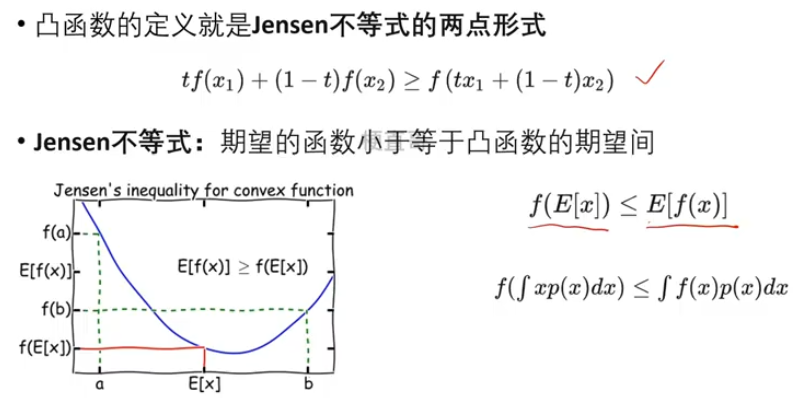
Jensen不等式

三、梯度下降

3.1、搜索逼近策略

??????? 先确定方向：梯度????????再确定步长：学习率

?????????

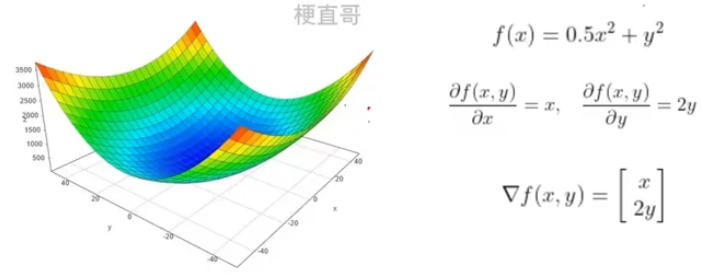
3.2、梯度

????????梯度就是函数曲面的陡度,偏导数是某个具体方向上的陡度

????????梯度就等于所有方向上偏导数的向量和

????????

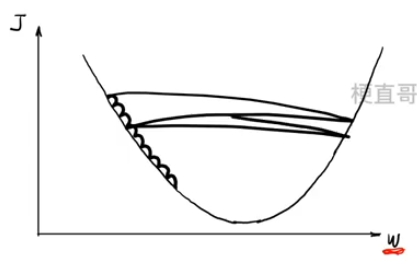
3.3、学习率

??????? 学习率太小，收敛慢

??????? 学习率太大，不收敛

????????

3.4、梯度下降法 —— 初始值、梯度、学习率

??????? ① 确定起始点

??????? ②计算

??????? ③控制好油门（学习率）~

?四、随机梯度下降法（Stochastic Gradient Descent）

?4.1、梯度下降法的问题

·不能保证被优化函数达到全局最优解
·全部训练数据上最小化损失，计算时间太长
·如果函数形态复杂，可能会在局部最小值附近来回震荡·对于初始值的选择非常敏感

4.2、SGD基本思想

·每次迭代中仅使用一个样本来计算梯度
·根据梯度来调整参数的值

?4.3、动态学习率

??????? 使用动态学习率可以帮助模型更快地收敛

????????

?五、小批量梯度下降法（Mini-Batch Stochastic Gradient Descent）

决定批量大小的因素

过大的批量虽然使得梯度估计更精确，但回报小
太小的批量难以充分利用多核架构
并行处理下，内存消耗和批量大小成正比
2的幂次方在使用GPU时可以提高效率，故取值32-256之间
注意：随机抽取

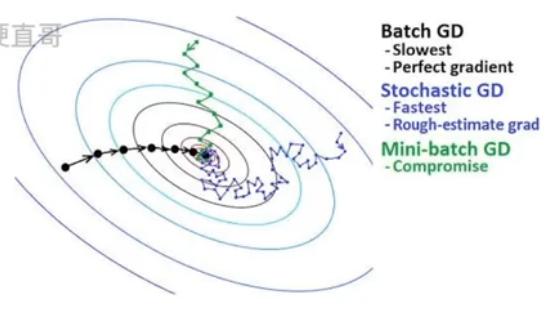
差别：

????????

代码实现：

import torch
import torch.nn as nn
import numpy as np
import matplotlib.pyplot as plt
from tqdm import *

# 定义模型和损失函数
class Model(nn.Module):
    def __init__(self):
        super().__init__()
        self.hidden1 = nn.Linear(1, 32)
        self.hidden2 = nn.Linear(32, 32)
        self.output = nn.Linear(32, 1)

    def forward(self, x):
        x = torch.relu(self.hidden1(x))
        x = torch.relu(self.hidden2(x))
        return self.output(x)
loss_fn = nn.MSELoss()

# 生成随机数据
np.random.seed(0)
n_samples = 1000
x = np.linspace(-5, 5, n_samples)
y = 0.3 * (x ** 2) + np.random.randn(n_samples)

# 转换为Tensor
x = torch.unsqueeze(torch.from_numpy(x).float(), 1)
y = torch.unsqueeze(torch.from_numpy(y).float(), 1)

# 将数据封装为数据集
dataset = torch.utils.data.TensorDataset(x, y)

names = ["Batch", "Stochastic", "Minibatch"] # 批量梯度下降法、随机梯度下降法、小批量梯度下降法
batch_size = [n_samples, 1, 128]
momentum= [1,0,1]
losses = [[], [], []]

# 超参数
learning_rate = 0.0001
n_epochs = 1000

# 分别训练
for i in range(3):
    model = Model()
    optimizer = torch.optim.SGD(model.parameters(), lr=learning_rate, momentum=momentum[i])
    dataloader = torch.utils.data.DataLoader(dataset, batch_size=batch_size[i], shuffle=True)
    for epoch in tqdm(range(n_epochs), desc=names[i], leave=True, unit=' epoch'):
        x, y = next(iter(dataloader))
        optimizer.zero_grad()
        out = model(x)
        loss = loss_fn(out, y)
        loss.backward()
        optimizer.step()
        losses[i].append(loss.item())

# 使用 Matplotlib 绘制损失值的变化趋势
for i, loss_list in enumerate(losses):
    plt.figure(figsize=(12, 4))
    plt.plot(loss_list)
    plt.ylim((0, 15))
    plt.xlabel('Epoch')
    plt.ylabel('Loss')
    plt.title(names[i])
    plt.show()

Batch: 100%|██████████| 1000/1000 [00:07<00:00, 129.91 epoch/s]
Stochastic: 100%|██████████| 1000/1000 [00:00<00:00, 2397.32 epoch/s]
Minibatch: 100%|██████████| 1000/1000 [00:01<00:00, 780.15 epoch/s]

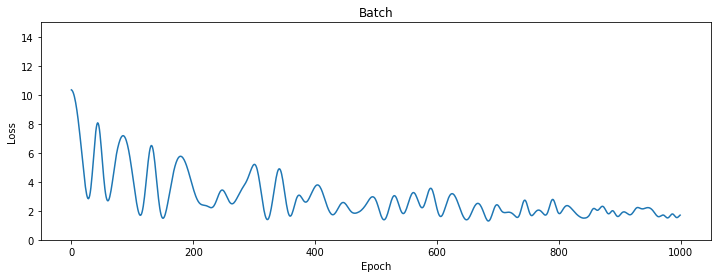
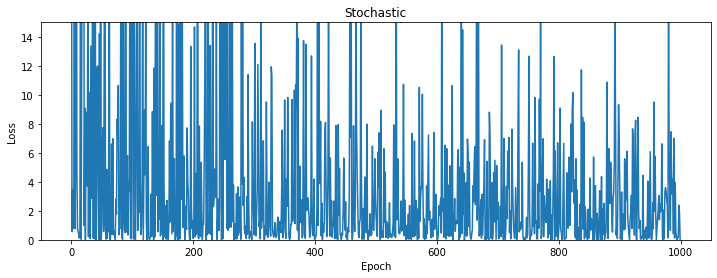
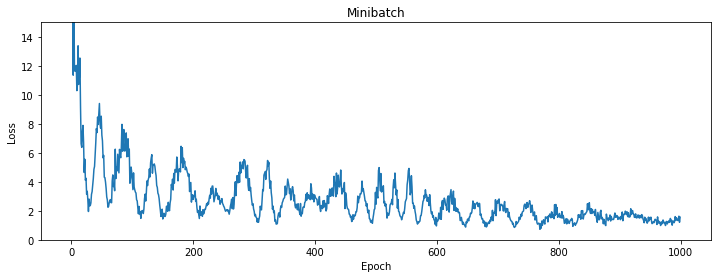
六、动量法

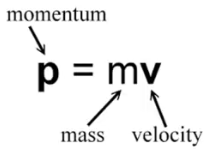
6.1、物理学中的动量

????????动量指的是这个物体在它运动方向上保持运动的趋势。

??????? 动量是一个向量。

????????????????

??????? 动量守恒定律：

????????????????

6.2、深度学习中的动量

????????一阶动量：过去各个时刻梯度的线性组合。

????????????????

????????二阶动量：过去各个时刻梯度的平方的线性组合。

?????????????????

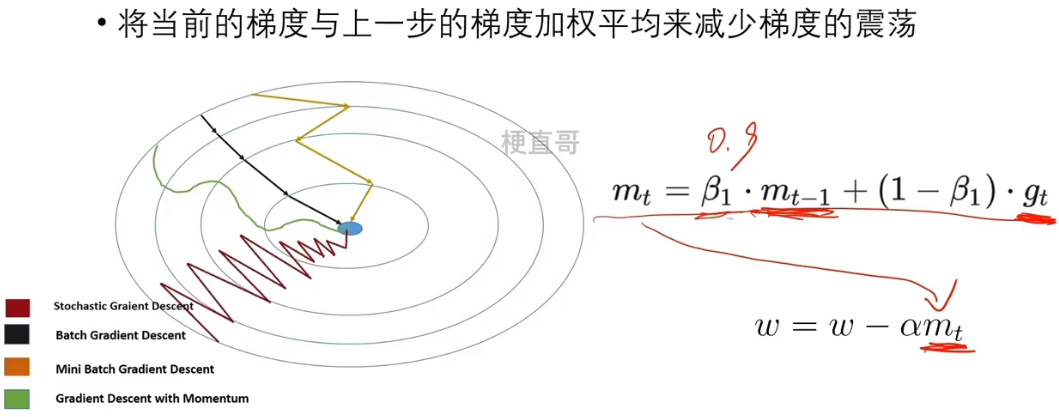
6.3、基本思想

????????将当前的梯度与上一步的梯度加权平均来减少梯度的震荡。

????????

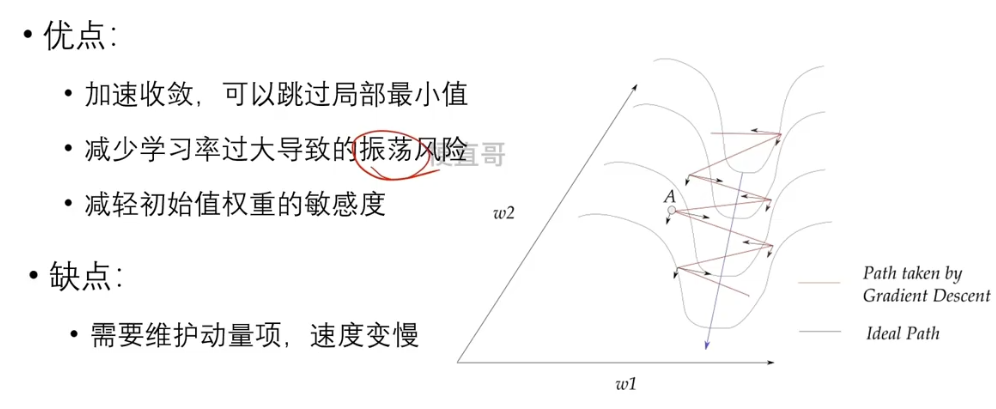
6.4、优缺点

????????

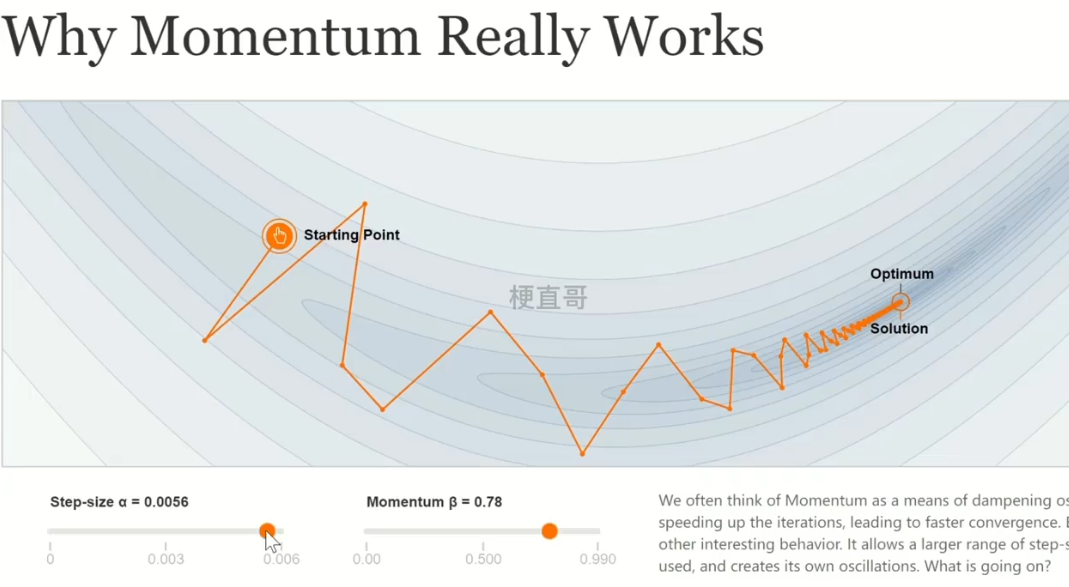
6.5、可视化网站：

????????

?七、AdaGrad算法

??????? 传统的SGD以及各种变种都是以同样的学习率来更新每个参数的，但是深度神经网络往往包含大量参数，而且这些参数并不总是用得到的。对于经常更新的参数，我们已经积累了大量知识，就不希望被新的样本影响太大，换句话说，就是对于更新很频繁的参数可以将学习率慢一些。

??????? 而对于更新慢的参数，我们了解到的信息太少，希望从每一个偶然出现的样本多学一些，也就是学习率大一些，

????????那怎么动态的度量历史更新的频率呢？

??????? ———— 二阶动量

7.1、基本思想

??????? 根据二阶动量动态调整学习率。

??????? gτ 为历史梯度值。有平方可以把正负去掉，累加。

????????

7.2、算法流程

??????? 1、计算目标函数关于当前参数的梯度 gt，根据历史梯度计算一阶动量 mt 和二阶动量 vt

??????? 2、计算当前时刻的下降梯度 η ，其中 α 为学习率，一般为了避免分母为零，会加上一个平方项。

????????

??????? 参数更新越频繁，二阶动量越大，学习率就越小。

??????? 3、进行梯度更新：

????????

?7.3、稀疏特征

????????指的是在很多样本中只有少数出现过的特征。

????????训练模型时，稀疏特征可能很少更新，导致训练不出理想结果。

7.4、优缺点

????????

7.5、代码实现

import torch
import matplotlib.pyplot as plt

# 假设我们有一个简单的线性回归模型
# y = w * x + b
# 其中 w 和 b 是需要学习的参数

# 定义超参数
learning_rate = 0.01
num_epochs = 100

# 随机生成训练数据
X = torch.randn(100, 1)
y = 2 * X + 3 + torch.randn(100, 1)

# 初始化参数
w = torch.zeros(1, requires_grad=True)
b = torch.zeros(1, requires_grad=True)

# 创建 Adagrad optimizer
optimizer = torch.optim.Adagrad([w, b], lr=learning_rate)

# 记录每次迭代的 loss
losses = []

# 训练模型
for epoch in range(num_epochs):
  # 计算预测值
  y_pred = w * X + b

  # 计算 loss
  loss = torch.mean((y_pred - y) ** 2)

  # 记录 loss
  losses.append(loss.item())

  # 清空上一步的梯度
  optimizer.zero_grad()

  # 计算梯度
  loss.backward()

  # 更新参数
  optimizer.step()

# 可视化训练过程
plt.plot(losses)
plt.xlabel('Epoch')
plt.ylabel('Loss')
plt.show()

?八、RMSProp / AdaDelta算法

两种对二阶动量进行优化的方法基本思想

????????时序累加修改二阶动量，动态调整学习率

RMSProp 2012年提出

??????? AdaGrad单调递减的学习率变化过于激进，所以

????????改变二阶动量计算方法的策略：

????????????????不累积全部历史梯度，而只关注过去一段时间窗口的下降梯度。

??????? β2 叫做衰减率系数。

?????????

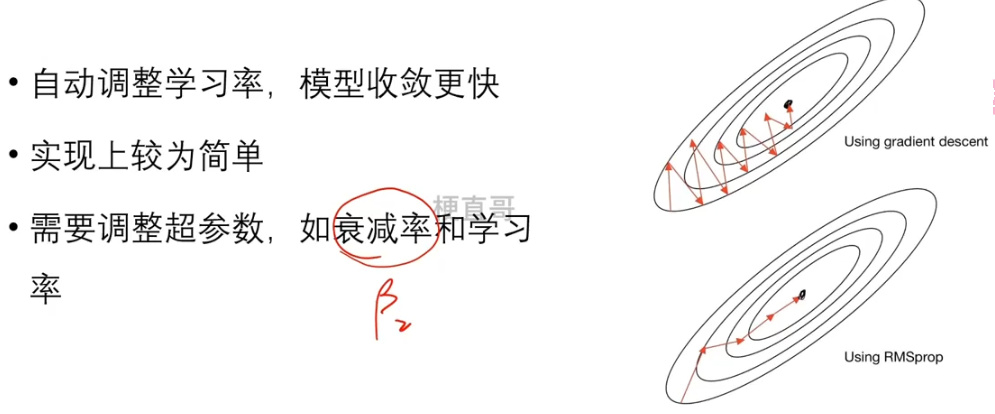
优缺点

?????????

AdaDelta 2011年提出

??????? 避免使用手动调整学习率的方法来控制训练过程，而是自动调整学习率，

????????使得训练过程更加顺畅。

??????? 主要由两部分组成：

??????????????? 梯度的积分和更新的规则。

??????????????? 梯度积分：对梯度进行累加并记录

????????

?优缺点

????????

?九、Adam算法 ***

9.1、基本思想

????????把一阶动量和二阶动量都用起来，Adaptive + Momentum

??????????????? gt 当前时间步的梯度

??????????????? mt 和 vt 一阶二阶矩估计向量（一阶二阶动量）

??????????????? β1 β2 两个衰减率的超参数，一般取值 0.9/0.999

??????????????? 偏差校正即更新 mt 和 vt

??????????????? 更新 θt ，ε保证分母不会等于0

????????

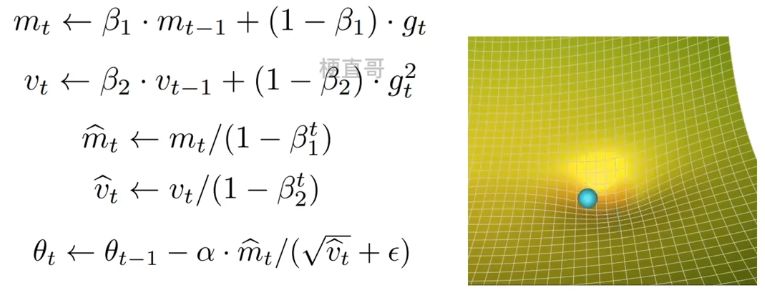
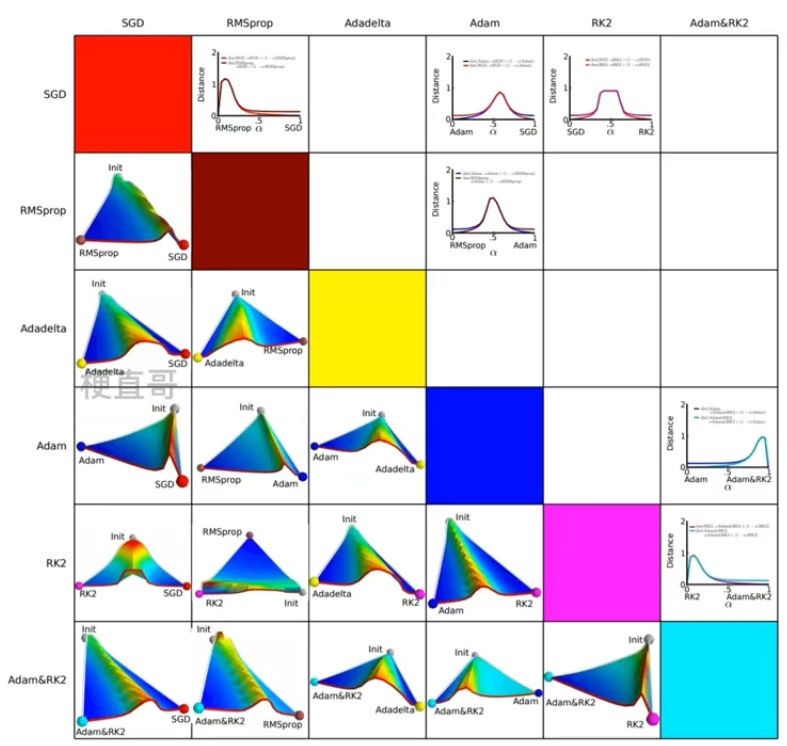
?9.2、梯度下降法及其变体关系

????????

9.3、原理框架流程

?????????定义优化参数w，目标函数f(w)，初始学习率 α
????????开始每个epoch迭代优化：
??????????????? 1、计算目标函数当前梯度

????????????????????????
??????????????? 2、根据历史梯度计算一阶动量和二阶动量

????????????????????????

????????????????3、计算当前时刻参数更新量

????????????????????????

??????????????? 4、迭代更新权重参数

????????????????????????

?不同的优化算法为什么效果差这么多？

9.4、核心差异

??????? 区别在于下降方向。

??????? 前半部分是学习率（下降步长），后半部分是下降方向。

??????? SGD的下降方向就是该位置梯度方向的反方向；

??????? 自适应学习率算法 RMSprop 为每个参数设定了不同的学习率，因此下降方向是缩放过的一阶动量的方向。

????????

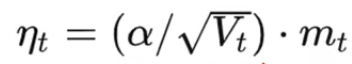
??????? 下图中，横坐标表示降维后的特征空间，区域的颜色表示目标函数值的变化。

????????

9.5、最优选择策略讨论

????????不想做精细的调优，那么Adam；

????????更加自如地控制优化迭代的各类参数，那么SGD；

????????先用Adam快速下降，再用SGD调优；

????????算法美好，数据王道!?

????????

?十、梯度下降代码实现

10.1 梯度下降过程

10.1.1、二维平面内的梯度下降

# 导入必要的库
import torch
import matplotlib.pyplot as plt

# 定义函数
def f(x):
    return x ** 2 + 4 * x + 1

# 定义初始值
x = torch.tensor(-10., requires_grad=True)

# 迭代更新参数
learning_rate = 0.9

# 用于记录每一步梯度下降的值
xs = []
ys = []

# 开始迭代
for i in range(100):
    # 计算预测值和损失
    y = f(x)

    # 记录参数和损失
    xs.append(x.item())
    ys.append(y.item())

    # 反向传播求梯度
    y.backward()

    # 更新参数
    with torch.no_grad():
        x -= learning_rate * x.grad

        # 梯度清零
        x.grad.zero_()
        
# 打印结果
print(f'最终参数值：{x.item()}')

最终参数值：-2.000000238418579

# 显示真实的函数曲线
x_origin = torch.arange(-10, 10, 0.1)
y_origin = f(x_origin)
plt.plot(x_origin, y_origin,'b-')

# 绘制搜索过程
plt.plot(xs,ys,'r--')
plt.scatter(xs, ys, s=50, c='r')  # 圆点大小为 50，颜色为红色
plt.xlabel('x')
plt.ylabel('y')
plt.show()

10.1.2 三维平面内的梯度下降

# 定义函数
def f(x, y):
    return x ** 2 + 2* y ** 2

# 定义初始值
x = torch.tensor(-10., requires_grad=True)
y = torch.tensor(-10., requires_grad=True)

# 记录每一步的值
xs = []
ys = []
zs = []

# 迭代更新参数
learning_rate = 0.1

# 开始迭代
for i in range(100):
    # 计算预测值和损失
    z = f(x, y)

    # 记录参数和损失
    xs.append(x.item())
    ys.append(y.item())
    zs.append(z.item())

    # 反向传播
    z.backward()

    # 更新参数
    x.data -= learning_rate * x.grad
    y.data -= learning_rate * y.grad

    # 清空梯度
    x.grad.zero_()
    y.grad.zero_()

# 打印结果
print(f'最终参数值：x={x.item()}, y={y.item()}')

最终参数值：x=-2.0370367614930274e-09, y=-6.533180924230175e-22

# 绘制图像
ax = plt.figure().add_subplot(projection='3d')
ax.plot(xs, ys, zs, 'r-')
ax.scatter(xs, ys, zs, s=50, c='r')  # 圆点大小为 50，颜色为红色

plt.show()

# 绘制原始的二维函数图像
X, Y = torch.meshgrid(torch.arange(-10, 10, 0.1), torch.arange(-10, 10, 0.1), indexing='ij')
Z = f(X, Y)
plt.contour(X, Y, Z, levels=30)

# 绘制搜索过程曲线
plt.plot(xs, ys, 'r-')
plt.scatter(xs, ys, s=50, c='r')  # 圆点大小为 50，颜色为红色
plt.show()

10.2. 不同优化器效果对比

# 导入必要的库
import torch.nn as nn
from torch.utils.data import DataLoader, TensorDataset  # 用于构造数据加载器
from torch.utils.data import random_split # 用于划分数据集
import torch.optim as optim

# 定义函数
def f(x, y):
    return x ** 2 + 2 * y ** 2

# 定义初始值
num_samples = 1000 # 1000个样本点
X = torch.rand(num_samples) # 均匀分布
Y = torch.rand(num_samples) # 均匀分布
Z = f(X,Y) +  torch.randn(num_samples)  #高斯分布扰动项

dataset = torch.stack([X, Y, Z], dim = 1)
dataset[0]

tensor([0.3720, 0.4497, 1.0605])

# 按照8：2划分数据集
train_size = int(0.8 * len(dataset))
test_size = len(dataset) - train_size

train_dataset, test_dataset = random_split(dataset=dataset, lengths=[train_size, test_size])

# 将数据封装成数据加载器
train_dataloader = DataLoader(TensorDataset(train_dataset.dataset.narrow(1,0,2), train_dataset.dataset.narrow(1,2,1)),
                              batch_size=32, shuffle=False)
test_dataloader = DataLoader(TensorDataset(test_dataset.dataset.narrow(1,0,2), test_dataset.dataset.narrow(1,2,1)),
                             batch_size=32, shuffle=False)

# 定义一个简单模型
class Model(nn.Module):
    def __init__(self):
        super().__init__()
        self.hidden = nn.Linear(2, 8)
        self.output = nn.Linear(8, 1)

    def forward(self, x):
        x = torch.relu(self.hidden(x))
        return self.output(x)

# 定义损失函数
loss_fn = nn.MSELoss()

# 初始化模型序列
opt_labels = ['SGD', 'Momentum', 'Adagrad', 'RMSprop', 'Adadelta', 'Adam']
models = [Model(), Model(), Model(), Model(), Model(), Model()] 

# 优化器列表
SGD = optim.SGD(models[0].parameters(), lr=learning_rate)
Momentum = optim.SGD(models[1].parameters(), lr=learning_rate, momentum=0.8, nesterov=True)
Adagrad = optim.Adagrad(models[2].parameters(), lr=learning_rate)
RMSprop = optim.RMSprop(models[3].parameters(), lr=learning_rate)
Adadelta = optim.Adadelta(models[4].parameters(), lr=learning_rate)
Adam = optim.Adam(models[5].parameters(), lr=learning_rate)
opts = [SGD, Momentum, Adagrad, RMSprop, Adadelta, Adam]

# 定义训练和测试误差历史记录数组
train_losses_his = [[],[],[],[],[],[]]
test_losses_his = [[],[],[],[],[],[]]

# 超参数
num_epochs = 50
learning_rate = 0.01 # 学习率

# 模型训练和测试
for epoch in range(num_epochs):
    # 当前epoch每个模型在训练集上的总损失列表
    train_losses = [0,0,0,0,0,0]
    # 遍历训练集
    for inputs, targets in train_dataloader:
        # 迭代不同的模型
        for index, model, optimizer, loss_history in zip(range(6), models, opts, train_losses_his):
            # 预测、损失函数、反向传播
            model.train()
            outputs = model(inputs)
            loss = loss_fn(outputs, targets)
            optimizer.zero_grad()
            loss.backward()
            optimizer.step()
            # 记录loss
            train_losses[index] += loss.item()

    
    # 当前epoch每个模型在训测试集上的总损失列表
    test_losses = [0,0,0,0,0,0]
    # 在测试数据上评估，测试模型不计算梯度
    with torch.no_grad():
        # 遍历测试集
        for inputs, targets in test_dataloader:
            # 迭代不同的模型
            for index, model, optimizer, loss_history in zip(range(6), models, opts, test_losses_his):
            # 预测、损失函数、反向传播
                model.eval()
                outputs = model(inputs)
                loss = loss_fn(outputs, targets)
                test_losses[index] += loss.item()
    
    # 计算loss并记录到历史记录中
    for i in range(6):
        train_losses[i] /= len(train_dataloader)
        train_losses_his[i].append(train_losses[i])
        test_losses[i] /= len(test_dataloader)
        test_losses_his[i].append(test_losses[i])

# 绘制训练集损失曲线
for i, l_his in enumerate(train_losses_his):
    plt.plot(l_his, label=opt_labels[i])
plt.legend(loc='best')
plt.xlabel('Epochs')
plt.ylabel('Loss')
plt.show()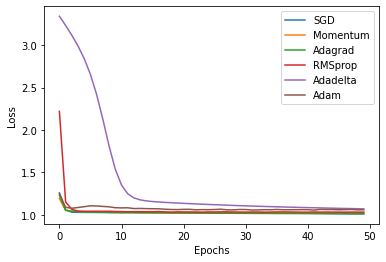

# 绘制测试集损失曲线
for i, l_his in enumerate(test_losses_his):
    plt.plot(l_his, label=opt_labels[i])
plt.legend(loc='best')
plt.xlabel('Epochs')
plt.ylabel('Loss')
plt.show()

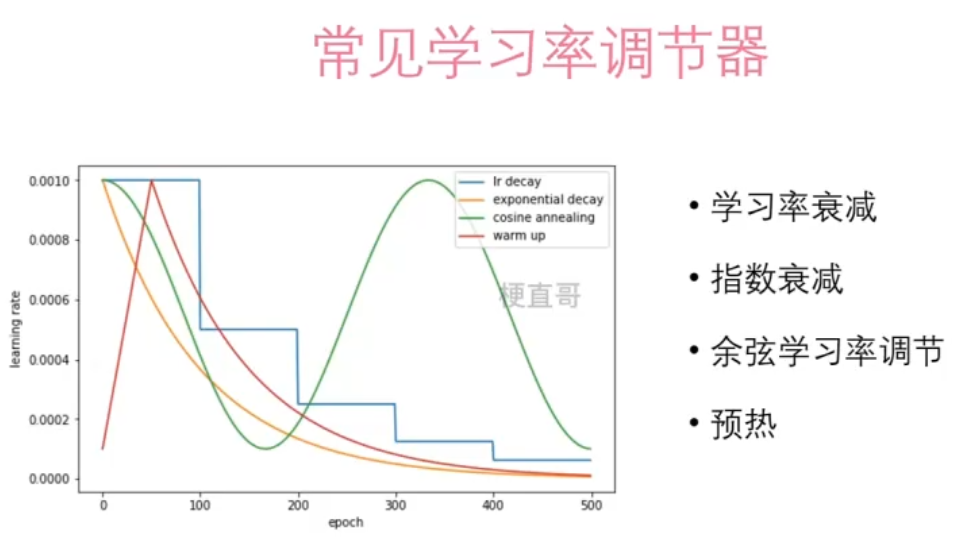
?十一、学习率调节器

需要考虑的因素：

????????

????????学习率是各类优化算法中的最关键的参数之一；

????????学习率调节器能够在训练过程中动态调整学习率。

????????

11.2、代码实现

# 导入必要的库
import torch
import numpy as np
import matplotlib.pyplot as plt
import torch.nn as nn
from torch.utils.data import DataLoader, TensorDataset # 用于构造数据加载器
from torch.utils.data import random_split # 用于划分数据集

11.2.1、数据生成

# 定义函数
def f(x, y):
    return x ** 2 + 2 * y ** 2

# 定义初始值
num_samples = 1000 # 1000个样本点
X = torch.rand(num_samples) # 均匀分布
Y = torch.rand(num_samples) # 均匀分布
Z = f(X,Y) + 3 * torch.randn(num_samples)

dataset = torch.stack([X, Y, Z], dim = 1)

11.2.3、数据划分

# 按照7：3划分数据集
train_size = int(0.7 * len(dataset))
test_size = len(dataset) - train_size

train_dataset, test_dataset = random_split(dataset=dataset, lengths=[train_size, test_size])

# 将数据封装成数据加载器
train_dataloader = DataLoader(TensorDataset(train_dataset.dataset.narrow(1,0,2), train_dataset.dataset.narrow(1,2,1)), batch_size=32)
test_dataloader = DataLoader(TensorDataset(test_dataset.dataset.narrow(1,0,2), test_dataset.dataset.narrow(1,2,1)), batch_size=32)

11.2.4、模型定义

# 定义一个简单模型
class Model(nn.Module):
    def __init__(self):
        super().__init__()
        self.hidden = nn.Linear(2, 8)
        self.output = nn.Linear(8, 1)

    def forward(self, x):
        x = torch.relu(self.hidden(x))
        return self.output(x)

11.2.5、模型训练对比

# 超参数
num_epochs = 100
learning_rate = 0.1 # 学习率，故意调大一些更直观

# 定义损失函数
loss_fn = nn.MSELoss()

# 通过一个训练对比有无学习率调节器的效果
for with_scheduler in [False, True]:

    # 定义训练和测试误差数组
    train_losses = []
    test_losses = []

    # 初始化模型
    model = Model()

    # 定义优化器
    optimizer = torch.optim.SGD(model.parameters(), lr=learning_rate)

    # 定义学习率调节器
    scheduler = torch.optim.lr_scheduler.ExponentialLR(optimizer, gamma=0.99)

    # 迭代训练
    for epoch in range(num_epochs):
        # 在训练数据上迭代
        model.train()
        train_loss = 0
        # 遍历训练集
        for inputs, targets in train_dataloader:
            # 预测、损失函数、反向传播
            optimizer.zero_grad()
            outputs = model(inputs)
            loss = loss_fn(outputs, targets)
            loss.backward()
            optimizer.step()
            # 记录loss
            train_loss += loss.item()

        # 计算loss并记录到训练误差
        train_loss /= len(train_dataloader)
        train_losses.append(train_loss)

        # 在测试数据上评估，测试模型不计算梯度
        model.eval()
        test_loss = 0
        with torch.no_grad():
            # 遍历测试集
            for inputs, targets in test_dataloader:
                # 预测、损失函数
                outputs = model(inputs)
                loss = loss_fn(outputs, targets)
                # 记录loss
                test_loss += loss.item()

            # 计算loss并记录到测试误差
            test_loss /= len(test_dataloader)
            test_losses.append(test_loss)

        # 是否更新学习率
        if with_scheduler:
            scheduler.step()
    
    # 绘制训练和测试误差曲线
    plt.figure(figsize=(8, 4))
    plt.plot(range(num_epochs), train_losses, label="Train")
    plt.plot(range(num_epochs), test_losses, label="Test")
    plt.title("{0} lr_scheduler".format("With" if with_scheduler else "Without"))
    plt.legend()
#     plt.ylim((1, 2))
    plt.show()

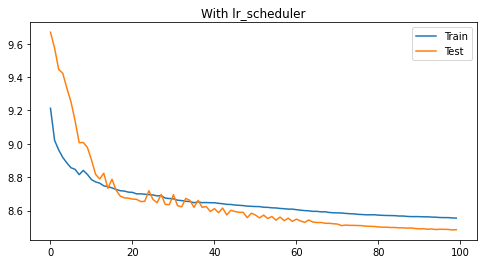
11.2.6、常见学习率调节器

# 学习率衰减，例如每训练100次就将学习率降低为原来的一半
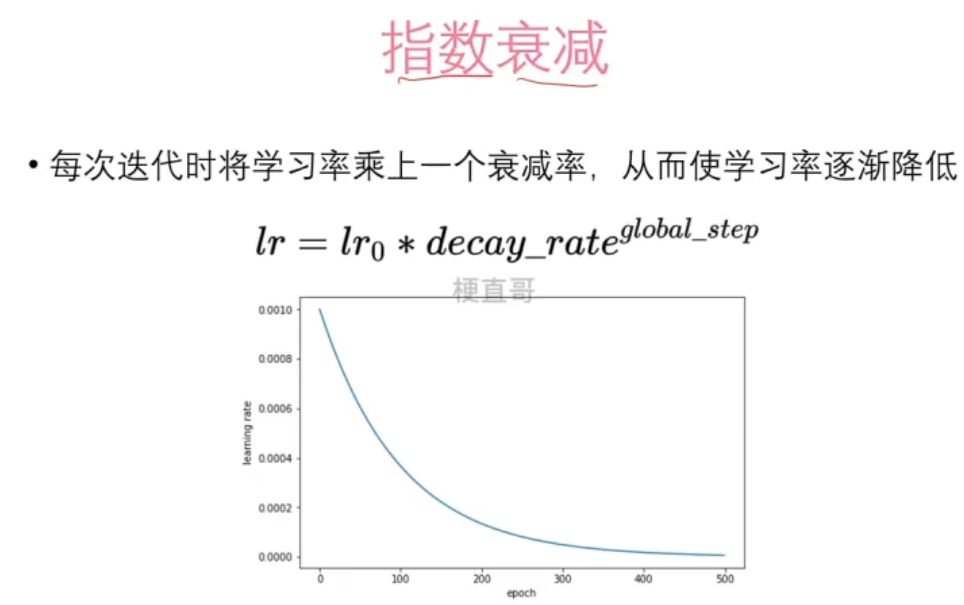
scheduler = torch.optim.lr_scheduler.StepLR(optimizer, step_size=100, gamma=0.5)

# 指数衰减法，每次迭代将学习率乘上一个衰减率
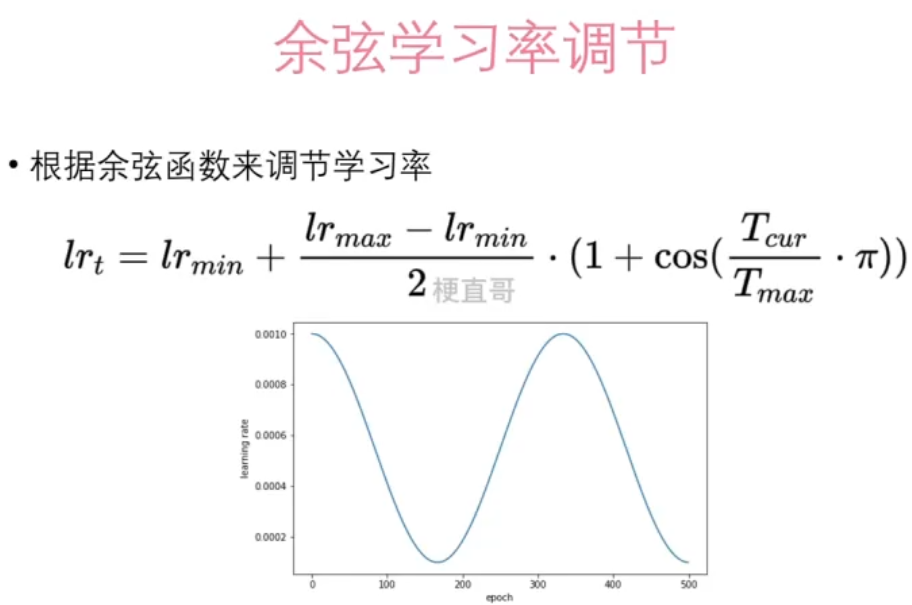
scheduler = torch.optim.lr_scheduler.ExponentialLR(optimizer, gamma=0.99)

# 余弦学习率调节，optimizer初始学习率为最大学习率，eta_min是最小学习率，T_max是最大迭代次数
scheduler = torch.optim.lr_scheduler.CosineAnnealingLR(optimizer, T_max=100, eta_min=0.00001)

# 自定义学习率，通过一个lambda函数实现自定义的学习率调节器
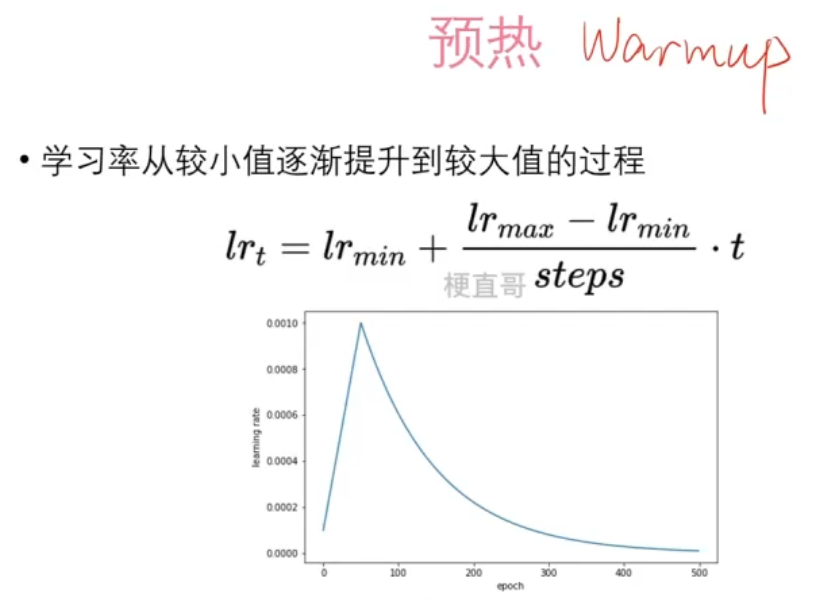
scheduler = torch.optim.lr_scheduler.LambdaLR(optimizer, lr_lambda=lambda epoch: 0.99 ** epoch)

# 预热
warmup_steps = 20
scheduler = torch.optim.lr_scheduler.LambdaLR(optimizer, lr_lambda=lambda t: min(t / warmup_steps, 0.001))

参考

深度学习必修课：进击算法工程师【梗直哥瞿炜】_哔哩哔哩_bilibili

Deep-Learning-Code: 《深度学习必修课：进击算法工程师》配套代码 - Gitee.com

文章来源:https://blog.csdn.net/weixin_47187147/article/details/135024186
本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若内容造成侵权/违法违规/事实不符，请联系我的编程经验分享网邮箱：chenni525@qq.com进行投诉反馈，一经查实，立即删除！

深度学习 | 梯度下降算法及其变体

一、最优化与深度学习

?1.3、优化中的挑战

?????? 1.3.1、局部最小值

??????? 1.3.2、 鞍点

??????? 1.3.3、悬崖

???????? 1.3.4、长期依赖问题

二、损失函数

2.3、损失函数的性质

三、梯度下降

?四、随机梯度下降法（Stochastic Gradient Descent）

4.2、SGD基本思想

?4.3、动态学习率

?五、小批量梯度下降法（Mini-Batch Stochastic Gradient Descent）

六、动量法

6.2、深度学习中的动量

6.3、基本思想

?七、AdaGrad算法

7.1、基本思想

?7.3、稀疏特征

?八、RMSProp / AdaDelta算法

?九、Adam算法 ***

9.1、基本思想

9.3、原理框架流程

9.4、核心差异

9.5、最优选择策略讨论

?十、梯度下降代码实现

10.1 梯度下降过程

10.1.1、二维平面内的梯度下降

10.1.2 三维平面内的梯度下降

10.2. 不同优化器效果对比

?十一、学习率调节器

11.2、代码实现

11.2.1、数据生成

11.2.3、数据划分

11.2.4、模型定义

11.2.5、模型训练对比

11.2.6、常见学习率调节器

??????? 1.3.2、鞍点